- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Системы линейных уравнений с двумя переменными (7класс)
Содержание
- 1. Презентация по алгебре Системы линейных уравнений с двумя переменными (7класс)
- 2. Алгебра стоит на четырёх китахЧислоУравнениеТождествоФункция
- 3. ОпределениеУравнение – это равенство, содержащее одну или
- 4. Система уравнений и её решениеОпределенияСистемой уравнений называется
- 5. Способы решения систем уравнений
- 6. Решение системы способом подстановки7х - 2х - 4 = 1;5х = 5;х=1;Ответ: х=1; у=6.
- 7. Способ подстановки (алгоритм)Из какого-либо уравнения выразить одну
- 8. Решение системы способом сравненияПриравняемвыражениядля у7х - 1=2х+4,7х - 2х=4+1,5х=5,х=1.РешимуравнениеОтвет: (1; 6)
- 9. Способ сравнения (алгоритм)Выразить у через х (или
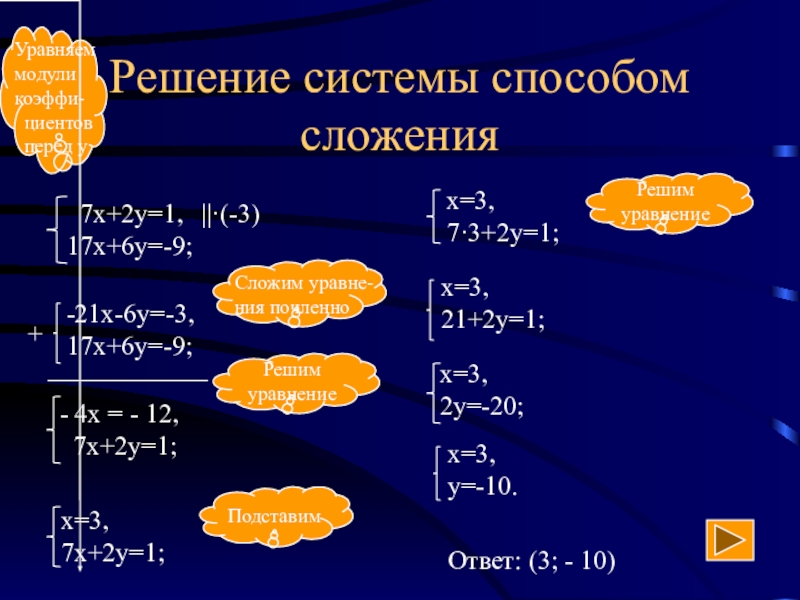
- 10. Решение системы способом сложения||·(-3)+____________Ответ: (3; - 10)
- 11. Способ сложения (алгоритм)Уравнять модули коэффициентов при какой-нибудь
- 12. Решение системы графическим способомy=10 - xy=x+2Выразим учерез хПостроим графикпервого уравненияу=х+2Построим графиквторого уравненияу=10 - хОтвет: (4; 6)
- 13. Графический способ (алгоритм)Выразить у через х в
- 14. -80Решение системы методом определителей
- 15. Метод определителей (алгоритм)Составить табличку (матрицу) коэффициентов при
- 16. Спасибо всем за работу
Алгебра стоит на четырёх китахЧислоУравнениеТождествоФункция
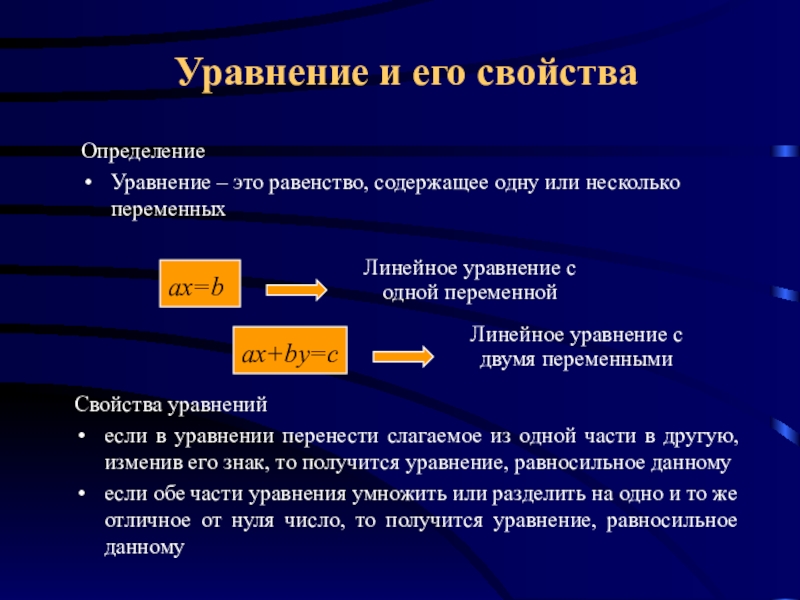
Слайд 3Определение
Уравнение – это равенство, содержащее одну или несколько переменных
Линейное уравнение с
одной
переменной
Линейное уравнение с
двумя переменными
Свойства уравнений
если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному
если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному
Уравнение и его свойства
Слайд 4Система уравнений и её решение
Определения
Системой уравнений называется некоторое количество уравнений, объединенных
фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Решить систему уравнений - это значит найти все её решения или установить, что их нет
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Решить систему уравнений - это значит найти все её решения или установить, что их нет
Слайд 7Способ подстановки (алгоритм)
Из какого-либо уравнения выразить одну переменную через другую
Подставить полученное
выражение для переменной в другое уравнение и решить его
Сделать подстановку найденного значения переменной и вычислить значение второй переменной
Записать ответ: х=…; у=… .
Сделать подстановку найденного значения переменной и вычислить значение второй переменной
Записать ответ: х=…; у=… .
Слайд 8Решение системы способом сравнения
Приравняем
выражения
для у
7х - 1=2х+4,
7х - 2х=4+1,
5х=5,
х=1.
Решим
уравнение
Ответ: (1; 6)
Слайд 9Способ сравнения (алгоритм)
Выразить у через х (или х через у) в
каждом уравнении
Приравнять выражения, полученные для одноимённых переменных
Решить полученное уравнение и найти значение одной переменной
Подставить значение найденной переменной в одно из выражений для другой переменной и найти её значение
Записать ответ: х=…; у=… .
Приравнять выражения, полученные для одноимённых переменных
Решить полученное уравнение и найти значение одной переменной
Подставить значение найденной переменной в одно из выражений для другой переменной и найти её значение
Записать ответ: х=…; у=… .
Слайд 11Способ сложения (алгоритм)
Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения системы
Составить
новую систему: одно уравнение новое, другое - одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .
Слайд 12Решение системы графическим способом
y=10 - x
y=x+2
Выразим у
через х
Построим график
первого уравнения
у=х+2
Построим график
второго
уравнения
у=10 - х
Ответ: (4; 6)
Слайд 13Графический способ (алгоритм)
Выразить у через х в каждом уравнении
Построить в одной
системе координат график каждого уравнения
Определить координаты точки пересечения
Записать ответ: х=…; у=… , или (х; у)
Определить координаты точки пересечения
Записать ответ: х=…; у=… , или (х; у)
Слайд 14-80
Решение системы методом определителей
Составим матрицу из
коэффициентов
при неизвестных Δ
при неизвестных Δ
= 7·6 - 2·17 = 42 - 34 = 8
= 1·6 - 2·(-9) = 6 + 18 = 24
= 7·(-9) - 1·17 = - 63 -17= -80
Составим определи-
тель Δx, заменив в определи-
теле Δ первый столбец
на столбец свободных
членов
Составим определи-
тель Δy, заменив в определи-
теле Δ второй столбец
на столбец свободных
членов
Δx
х=
Δ
=
24
8
=
3;
у=
Δy
Δ
=
8
= -10.
Найдем
х и у
Ответ: х=3; у= -10.
Слайд 15Метод определителей (алгоритм)
Составить табличку (матрицу) коэффициентов при неизвестных и вычислить определитель
Δ.
Найти - определитель Δx, получаемый из Δ заменой первого столбца на столбец свободных членов.
Найти - определитель Δy, получаемый из Δ заменой второго столбца на столбец свободных членов.
Найти значение переменной х по формуле Δx / Δ.
Найти значение переменной у по формуле Δy / Δ.
Записать ответ: х=…; у=… .
Найти - определитель Δx, получаемый из Δ заменой первого столбца на столбец свободных членов.
Найти - определитель Δy, получаемый из Δ заменой второго столбца на столбец свободных членов.
Найти значение переменной х по формуле Δx / Δ.
Найти значение переменной у по формуле Δy / Δ.
Записать ответ: х=…; у=… .
