- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Решение квадратных неравенств с помощью графика квадратичной функции
Содержание
- 1. Презентация по алгебре Решение квадратных неравенств с помощью графика квадратичной функции
- 2. Цели урокаСпособствовать выработке навыков и умений решения
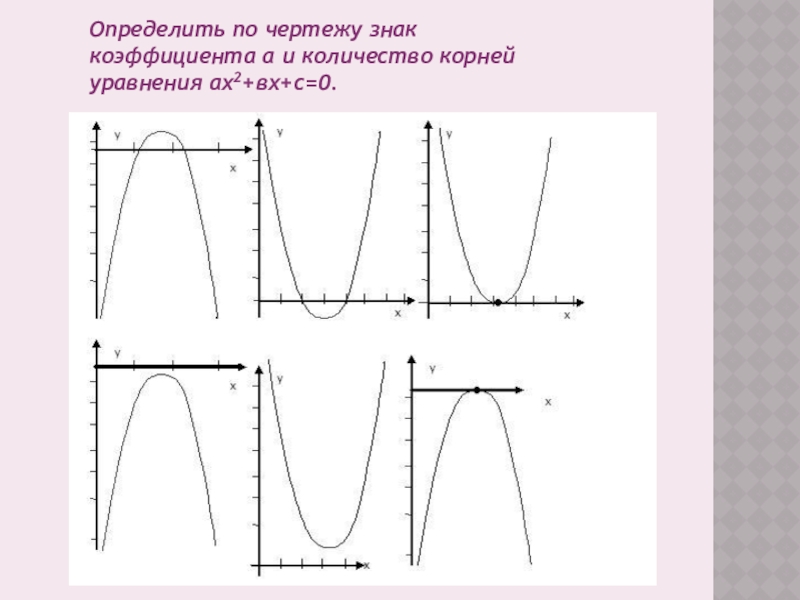
- 3. Определить по чертежу знак коэффициента a и количество корней уравнения ах2+вх+с=0.
- 4. На рисунке изображены графики квадратичных функций.По графику
- 5. Решить неравенство: (устно)х² + 10 > 0,х²
- 6. Решить неравенство: х2+4х-5≥0. 1. а=1>0 –
- 7. Графический способ основан на том, что левую
- 8. Отметить знаками «+» и « - »,
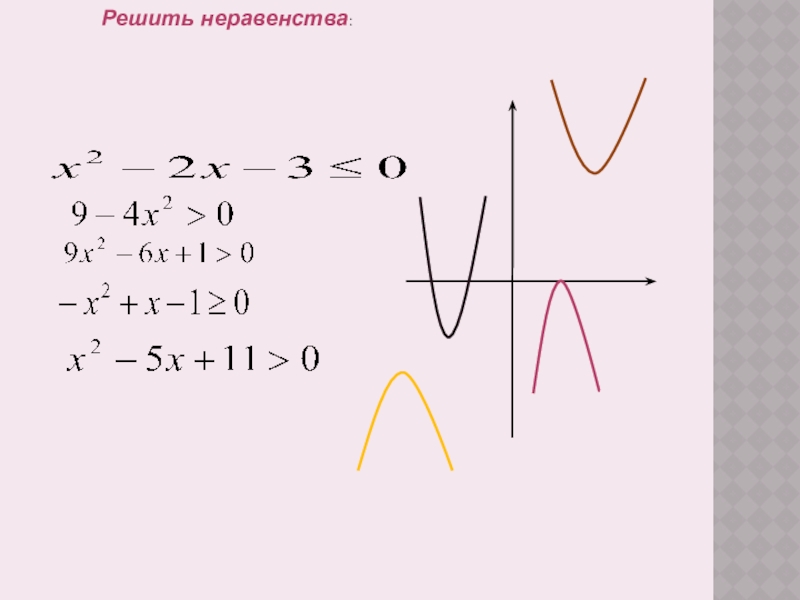
- 9. Решить неравенства:
- 10. Решение: 4).По графику видно, что парабола лежит
- 11. 1). Ветви вверх, a=9.2). D=0,значит корень в
- 12. 1). Ветви параболы направлены вверх, a=12). D=25-44=-19,
- 13. Самостоятельная работаРешить неравенства с помощью графика квадратичной функции
- 14. Слайд 14
- 15. 3х2+7х-6>01).а>0
- 16. Дополнительное задание
- 17. Домашнее задание § 41, выучить алгоритм №
- 18. Спасибо за урок!
Слайд 2Цели урока
Способствовать выработке навыков и умений решения квадратных неравенств графическим методом.
Отработать
Проверить знания учащихся в ходе самостоятельной работы.
Развивать логическое мышление и математический язык учащихся.
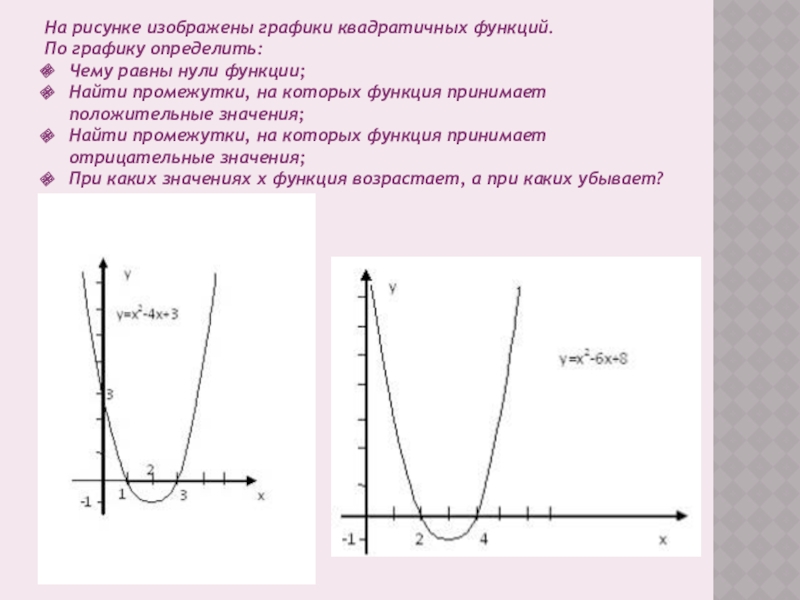
Слайд 4На рисунке изображены графики квадратичных функций.
По графику определить:
Чему равны нули функции;
Найти
Найти промежутки, на которых функция принимает отрицательные значения;
При каких значениях х функция возрастает, а при каких убывает?
Слайд 5Решить неравенство: (устно)
х² + 10 > 0,
х² + 9 < 0,
(
( х + 5 )² + 3 ≤ 0,
( х + 1 )² + 2 < 0,
0,5 х ² + 8 ≤ 0.
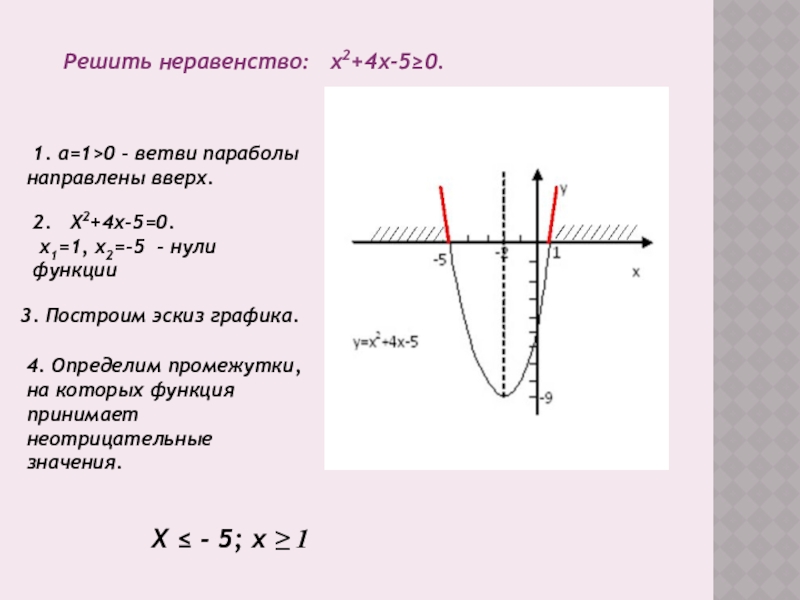
Слайд 6Решить неравенство: х2+4х-5≥0.
1. а=1>0 – ветви параболы направлены
2. Х2+4х-5=0.
х1=1, х2=-5 - нули функции
3. Построим эскиз графика.
4. Определим промежутки, на которых функция принимает неотрицательные значения.
Х ≤ - 5; х ≥ 1
Слайд 7Графический способ основан на том, что левую часть неравенства можно рассматривать
где для решения неравенства применяется нахождение промежутка знакопостоянства функции (промежуток, где функция сохраняет свой знак)
Слайд 8
Отметить знаками «+» и « - », интервалы на которых функция
Определить направление ветвей параболы.
Найти корни уравнения ах2+вх+с=0.
Построить эскиз графика, используя точки пересечения с осью ох
Алгоритм решения квадратного неравенства
Слайд 10Решение:
4).По графику видно, что парабола лежит ниже оси ох (значит,
.
Ответ: -1 ≤ х ≤ 3
1).a=-4, ветви направлены вниз.
(нули функции, они же точки пересечения параболы с осью ох)
4). По графику видно, что парабола лежит выше оси ох (функция принимает положительные значения), если -1,5 < Х < 1,5
3).Эскиз графика
2). (3-2х)(3+2х)=0,
Ответ: -1,5 < Х < 1,5
Слайд 111). Ветви вверх, a=9.
2). D=0,значит корень в уравнении один х =1/3
(точка касания с осью ох).
3).Эскиз графика
4). По рисунку видно, что неравенство будет верным при любых значениях x, кроме Х = 1/3
Ответ: Х < 1/3, Х > 1/3.
1). Ветви параболы направлены вниз, a=-1.
2). D=-3, значит, парабола не пересекает ось ох
( квадратный трёхчлен всюду отрицателен).
3). Эскиз графика
Ответ: решений нет ( пустое множество )
4). По рисунку видно, что неравенство будет верным ни при каких значениях Х.
Слайд 121). Ветви параболы направлены вверх, a=1
2). D=25-44=-19, корней нет (точек пересечения
3).Эскиз графика
4). По рисунку видно, что функция всюду положительна.
Ответ: х € R ( любое число )
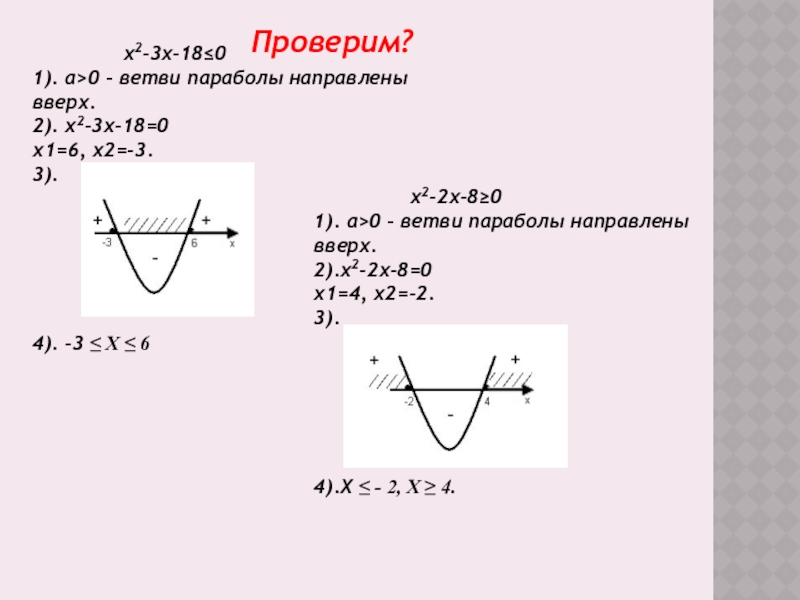
Слайд 14 х2-3х-18≤0
1). а>0 –
2). х2-3х-18=0
х1=6, х2=-3.
3).
4). -3 ≤ Х ≤ 6
х2-2х-8≥0
1). а>0 – ветви параболы направлены вверх.
2).х2-2х-8=0
х1=4, х2=-2.
3).
4).Х ≤ - 2, Х ≥ 4.
Проверим?
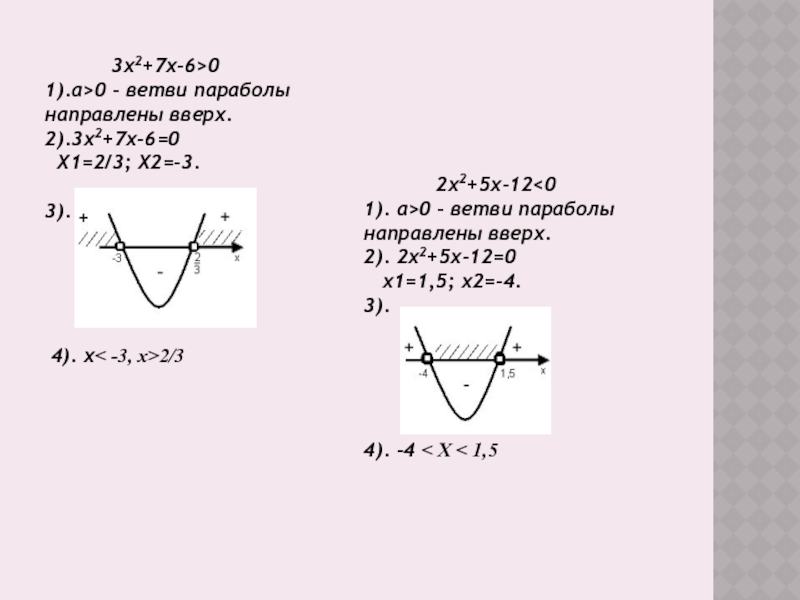
Слайд 15 3х2+7х-6>0
1).а>0 – ветви параболы направлены
2).3х2+7х-6=0
Х1=2/3; Х2=-3.
3).
4). х< -3, х>2/3
2х2+5х-12<0
1). а>0 – ветви параболы направлены вверх.
2). 2х2+5х-12=0
х1=1,5; х2=-4.
3).
4). -4 < Х < 1,5