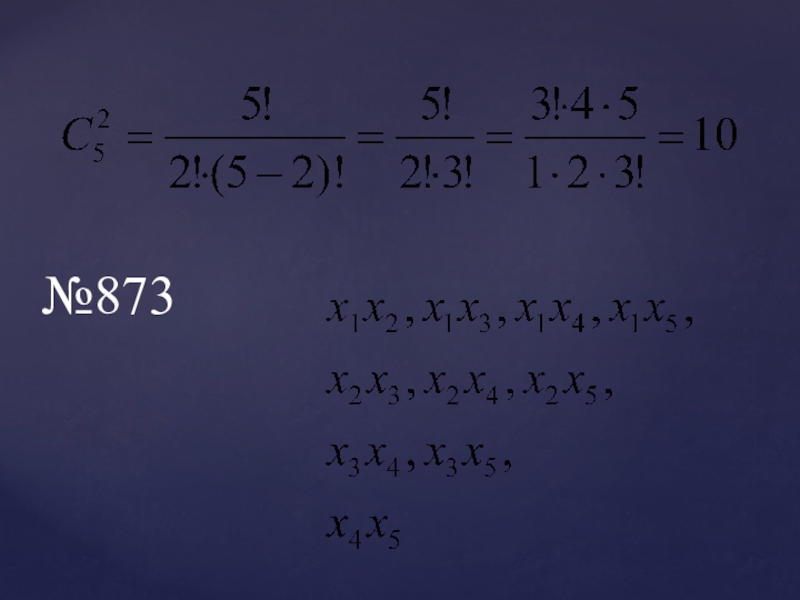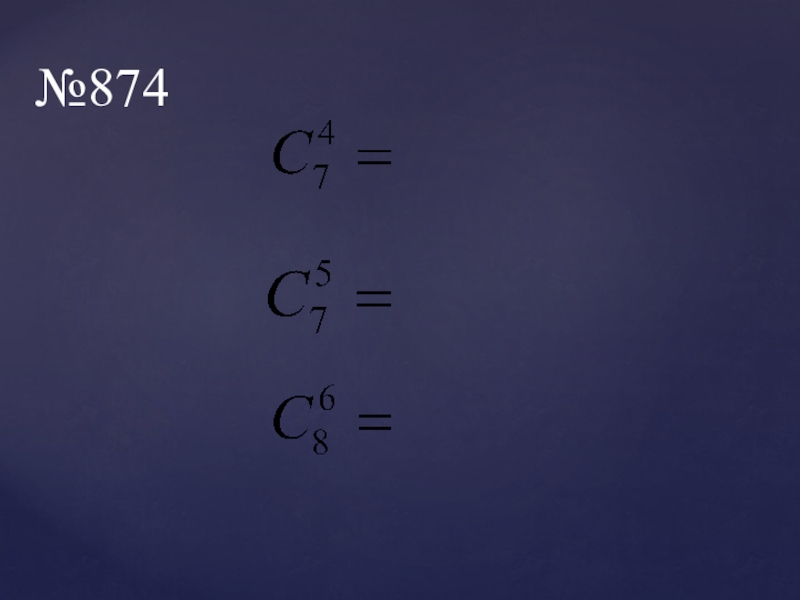- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Размещения и сочетания (9класс)
Содержание
- 1. Презентация по алгебре Размещения и сочетания (9класс)
- 2. Размещением из n элементов
- 3. РазмещенияНиже написаны все размещения из 3 элементов a, b, с по 2:
- 4. Сколькими способами можно распределить два билета на
- 5. Слайд 5
- 6. Слайд 6
- 7. №871
- 8. №872
- 9. №872
- 10. Сочетанием из n элементов по k называют
- 11. Сочетания
- 12. Пример 2. Сколькими различными способами из семи
- 13. Пример 3. Из перетасованной колоды, состоящей из
- 14. №873
- 15. №874
- 16. №874
- 17. №875 Докажите, что
- 18. №875 Вычислите:
- 19. №875 Вычислите:
- 20. Сколькими различными способами можно распределить между шестью лицами две разные путевки в санатории?№876
- 21. Сколькими способами можно распределить две одинаковые путевки между пятью лицами?№877
- 22. Сколькими способами можно присудить шести лицам три одинаковые премии?№878
- 23. Сколькими способами можно присудить шести лицам три одинаковые премии?№879
- 24. Иванов и Степанов входят в группу из
- 25. №880*Из перетасованной колоды, состоящей из 36 карт,
Размещением из n элементов по два называют любую упорядоченную пару, составленную из данных n элементов.Количество размещений из n элементов по два обозначают
Слайд 2Размещением из n элементов
по два называют любую упорядоченную пару, составленную из данных n элементов.
Количество размещений из n элементов по два обозначают через (по первой букве французского слова arrangement – размещение)
Количество размещений из n элементов по два обозначают через (по первой букве французского слова arrangement – размещение)
Размещения
Слайд 4Сколькими способами можно распределить два билета на разные кинофильмы между семью
друзьями?
Пример 1
Размещением из n элементов по k называют любой упорядоченный набор из k элементов, составленный из данных n элементов.
Слайд 10Сочетанием из n элементов по k называют любую группу из k
элементов, составленную из данных n элементов.
Число сочетаний из n элементов по k обозначают через
(по первой букве французского слова combination – сочетание).
Разница заключается в том, что если в размещении переставить местами элементы, то получится другое размещение, но сочетание не зависит от порядка входящих в него элементов.
Число сочетаний из n элементов по k обозначают через
(по первой букве французского слова combination – сочетание).
Разница заключается в том, что если в размещении переставить местами элементы, то получится другое размещение, но сочетание не зависит от порядка входящих в него элементов.
Сочетания
Слайд 12Пример 2. Сколькими различными способами из семи участников математического кружка можно составить
команду из двух человек для участия в олимпиаде?
Слайд 13Пример 3. Из перетасованной колоды, состоящей из 36 карт, наугад взяты 4
карты. Какова вероятность того, что все взятые карты тузы?
Слайд 20Сколькими различными способами можно распределить между шестью лицами две разные путевки
в санатории?
№876
Слайд 24Иванов и Степанов входят в группу из семи студентов, имеющих одинаковые
шансы получить один из двух разных призов. Какова вероятность того, что:
Иванов получит первый приз, а Степанов – второй;
Иванов и Степанов получат призы;
Иванов получит первый приз;
Иванов получит один из призов?
Иванов получит первый приз, а Степанов – второй;
Иванов и Степанов получат призы;
Иванов получит первый приз;
Иванов получит один из призов?
№879
Слайд 25№880*
Из перетасованной колоды, состоящей из 36 карт, наугад взяты 4 карты.
Какова вероятность того, в эту четверку:
попадут тузы бубен, пик, червей и треф в указанном порядке;
попадут 4 туза (в любом порядке);
попадет туз бубен и его возьмут первым;
попадет туз бубен?
попадут тузы бубен, пик, червей и треф в указанном порядке;
попадут 4 туза (в любом порядке);
попадет туз бубен и его возьмут первым;
попадет туз бубен?