«Школа здоровья и развития» г. Радужный
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре по теме Показательная функция
Содержание
- 1. Презентация по алгебре по теме Показательная функция
- 2. Определение показательной функцииПоказательной функцией называется функция у
- 3. 1) Например, в теории межпланетных путешествий решается
- 4. 2) Радиоактивный распад вещества задаётся формулой
- 5. 3) Изменение атмосферного давления p в зависимости
- 6. График показательной функции у = а
- 7. Свойства показательной функции у = а ,
- 8. График показательной функции у = а , 0
- 9. Свойства показательной функции у = а , 0
- 10. Показательная функция, её график и свойства
- 11. Если 0 < а < 1, то
- 12. Пример 1. Сравните числа 1,334 и 1,340.Общий
- 13. Пример 2. Решите графически уравнение 3х =4-х.Решение.Используем
- 14. Пример 3. Решите графически неравенство 3х >4-х.Решение.у=4-хИспользуем
- 15. Слайд 15
- 16. an ∙ am = an + m an
- 17. Если 0 < а < 1, то
- 18. Показательные уравненияУравнения вида af(x) = аh(х), где
- 19. Показательные уравнения. Примеры Пример 1Пример 2Пример 3
- 20. Показательные уравнения. Примеры Пример 4Пример 5
- 21. Показательные уравнения. Примеры Пример 6
- 22. Показательные уравнения. Примеры Пример 7
- 23. Показательные уравнения. Примеры Пример 8
- 24. Показательные уравнения. Примеры Пример 9 (однородное уравнение)
- 25. Показательные уравнения. Примеры Пример 10 (составление отношения)
- 26. Показательные уравнения. Примеры Пример 11 (скрытая замена переменной)+ = 4
- 27. Показательные уравнения. Примеры Пример 11 (скрытая замена переменной)+ = 4
- 28. Показательные неравенстваНеравенства вида af(x) > аh(х), где
- 29. Показательные неравенства. ПримерыПример 1Пример 2
- 30. Показательные неравенства. ПримерыПример 3
- 31. Показательные неравенства. ПримерыПример 4
Определение показательной функцииПоказательной функцией называется функция у = а , где а – заданное число, а>0, a ≠ 1. хПримеры:
Слайд 2Определение показательной функции
Показательной функцией называется функция у = а , где
а – заданное число, а>0, a ≠ 1.
х
Примеры:
Слайд 31) Например, в теории межпланетных путешествий решается задача об определении массы
топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости vo, с которой продукты горения вытекают из ракетного двигателя. Если не учитывать сопротивление воздуха и притяжение Земли, то масса
Показательная функция часто используется при описании различных физических процессов
топлива определяется формулой:
М = m(ev/vo-1) (формула К.Э. Циолковского).
Например, для того чтобы ракета с массой 1,5т имела скорость 8000м/с, надо взять примерно 80т топлива.
Слайд 42) Радиоактивный распад вещества задаётся формулой m = m0(1/2)t/tо,
где m и mо – масса радиоактивного вещества в момент времени t и в начальный момент времени t = 0; T - период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое).
Показательная функция часто используется при описании различных физических процессов
Когда радиоактивное вещество распадается, его количество уменьшается.
Через некоторое время остаётся половина первоначального количества вещества. Чем больше период полураспада, тем медленнее распадается вещество.
Слайд 53) Изменение атмосферного давления p в зависимости от высоты h над
уровнем моря описывается формулой p = pо ∙ ak, где pо – атмосферное давление над уровнем моря, а – некоторая постоянная.
Показательная функция часто используется при описании различных физических процессов
Барограф метеорологический
анероидный
Погодная станция Oregon Scientific
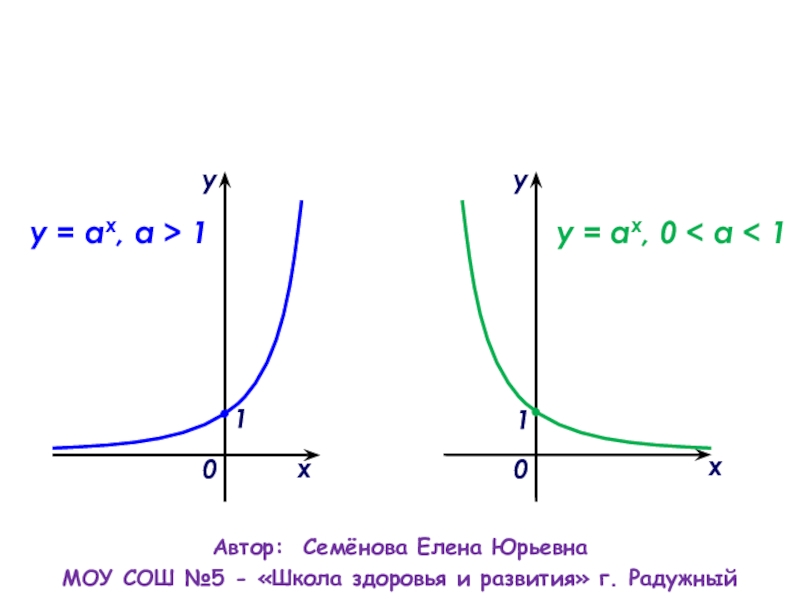
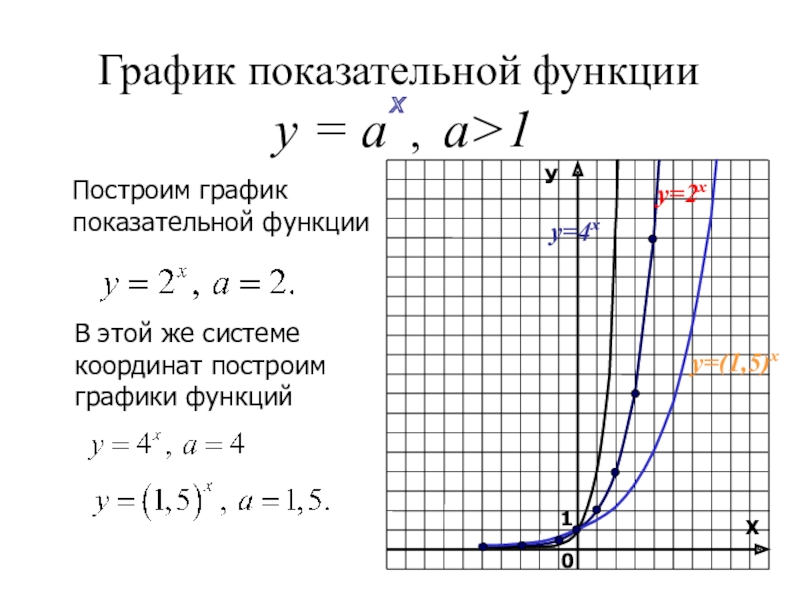
Слайд 6График показательной функции
у = а , а>1
Построим график показательной функции
В
этой же системе координат построим графики функций
У
Х
1
0
х
у=2х
у=(1,5)х
у=4х
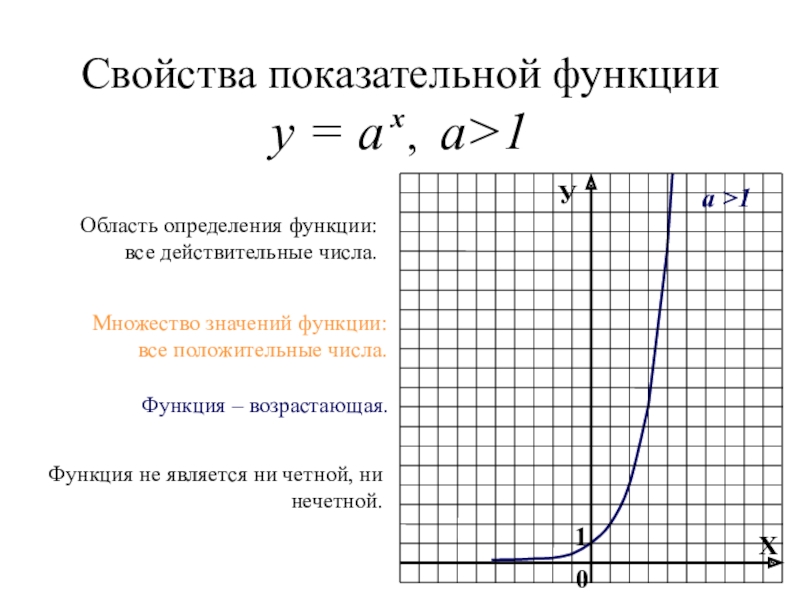
Слайд 7Свойства показательной функции у = а , а>1
х
Область определения функции:
все
действительные числа.
Множество значений функции:
все положительные числа.
Функция – возрастающая.
Функция не является ни четной, ни нечетной.
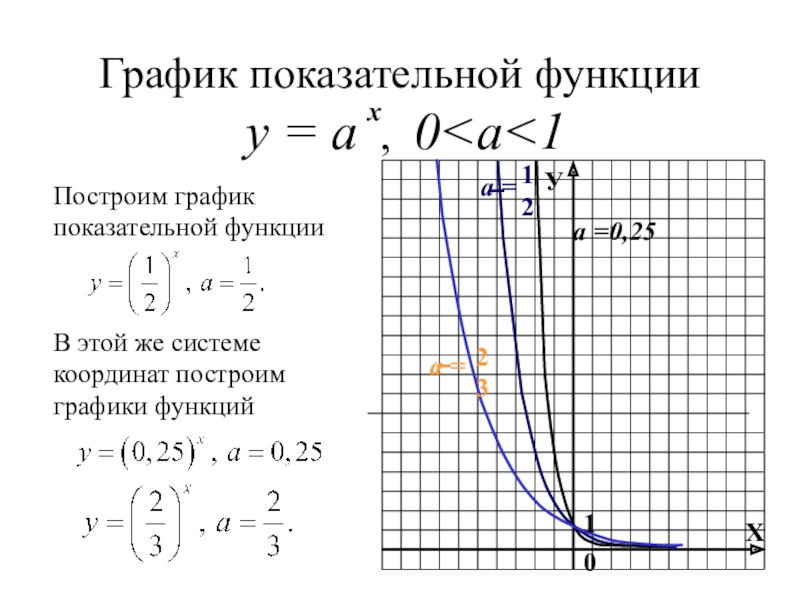
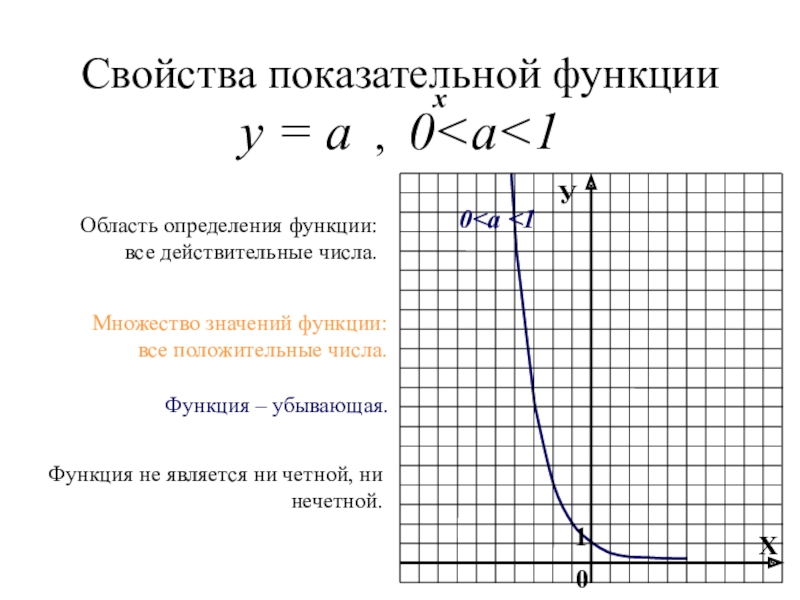
Слайд 8График показательной функции у = а , 0
этой же системе координат построим графики функций
У
Х
1
0
х
а =0,25
Слайд 9Свойства показательной функции у = а , 0
все действительные числа.
Множество значений функции:
все положительные числа.
Функция – убывающая.
Функция не является ни четной, ни нечетной.
Слайд 10Показательная функция,
её график и свойства
y
x
1
о
1) Область определения –
множество всех
действительных чисел (D(у)=R).
2) Множество значений – множество всех
положительных чисел (E(y)=R+).
3) Нулей нет.
4) у>0 при х R.
5) Функция ни чётная, ни нечётная.
6) Функция монотонна: возрастает на R при а>1
и убывает на R при 07) Наибольшего и наименьшего значений у функции нет.
8) Функция непериодична.
9) Ограничена снизу, не ограничена сверху.
действительных чисел (D(у)=R).
2) Множество значений – множество всех
положительных чисел (E(y)=R+).
3) Нулей нет.
4) у>0 при х R.
5) Функция ни чётная, ни нечётная.
6) Функция монотонна: возрастает на R при а>1
и убывает на R при 0
8) Функция непериодична.
9) Ограничена снизу, не ограничена сверху.
Слайд 11Если 0 < а < 1, то
a) неравенство ax >
1 справедливо ⟺ x < 0;
б) неравенство ax < 1 справедливо ⟺ x > 0.
б) неравенство ax < 1 справедливо ⟺ x > 0.
Свойства сравнения выражений вида ах, а ≠ 1, a > 0
Если 0 < а < 1 или а > 1, то равенство ar = as справедливо тогда и только тогда, когда r = s.
.
Если а > 1, то
a) неравенство ax > 1 справедливо ⟺ x > 0;
б) неравенство ax < 1 справедливо ⟺ x < 0.
Если а > 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) > h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) < h(x).
Если 0 < а < 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) < h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) > h(x).
Слайд 12Пример 1. Сравните числа 1,334 и 1,340.
Общий метод решения.
1. Представить числа
в виде степени с одинаковым основанием (если это необходимо)
1,334 и 1,340.
2. Выяснить, возрастающей или убывающей является показательная функция
а=1,3; а>1, след-но показательная функция возрастает.
3. Сравнить показатели степеней (или аргументы функций)
34<40.
4. Используя свойство возрастания (убывания) функции, сравнить степени с одинаковым основанием (или значения функций)
1,334 < 1,340.
5. Сравнить исходные числа.
1,334 и 1,340.
2. Выяснить, возрастающей или убывающей является показательная функция
а=1,3; а>1, след-но показательная функция возрастает.
3. Сравнить показатели степеней (или аргументы функций)
34<40.
4. Используя свойство возрастания (убывания) функции, сравнить степени с одинаковым основанием (или значения функций)
1,334 < 1,340.
5. Сравнить исходные числа.
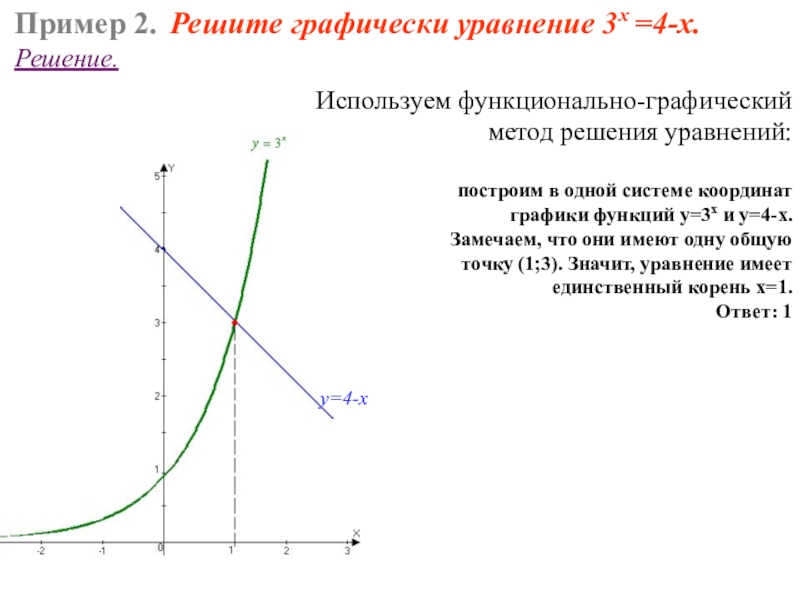
Слайд 13Пример 2. Решите графически уравнение 3х =4-х.
Решение.
Используем функционально-графический
метод решения уравнений:
построим в одной системе координат
графики функций у=3х и у=4-х.
Замечаем, что они имеют одну общую
точку (1;3). Значит, уравнение имеет
единственный корень х=1.
Ответ: 1
у=4-х
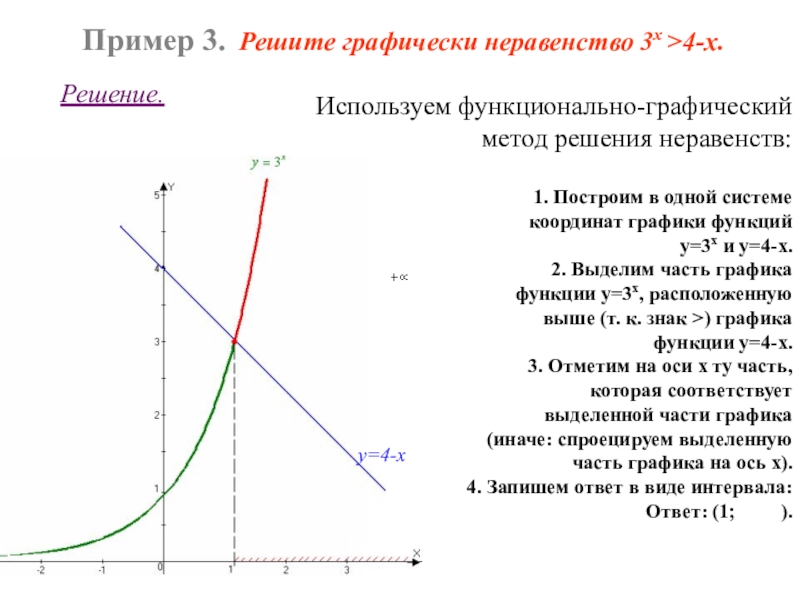
Слайд 14Пример 3. Решите графически неравенство 3х >4-х.
Решение.
у=4-х
Используем функционально-графический
метод решения неравенств:
1. Построим в одной системе
координат графики функций
у=3х и у=4-х.
2. Выделим часть графика
функции у=3х, расположенную
выше (т. к. знак >) графика
функции у=4-х.
3. Отметим на оси х ту часть,
которая соответствует
выделенной части графика
(иначе: спроецируем выделенную
часть графика на ось х).
4. Запишем ответ в виде интервала:
Ответ: (1; ).
Слайд 16an ∙ am = an + m
an : am = an
− m
(an)m = anm
(ab)n = an ∙ bn
(a : b)n = an : bn
(an)m = anm
(ab)n = an ∙ bn
(a : b)n = an : bn
а) При а > 1 функция возрастает на R;
б) при 0 < а < 1 функция убывает на R.
а) Нулей не имеет;
б) точка пересечения с осью ординат (0; 1),
т. к. у(0) = а0 = 1.
Свойства показательной функции y = ах, а ≠ 1, a > 0
Ни четная функция, ни нечетная.
D(y) = (-∞; +∞),
E(y) = (0; +∞).
.
Не ограничена сверху, ограничена снизу.
Не имеет ни наибольшего, ни наименьшего значений.
Непрерывна. Выпукла вниз.
Слайд 17Если 0 < а < 1, то
a) неравенство ax >
1 справедливо ⟺ x < 0;
б) неравенство ax < 1 справедливо ⟺ x > 0.
б) неравенство ax < 1 справедливо ⟺ x > 0.
Свойства сравнения выражений вида ах, а ≠ 1, a > 0
Если 0 < а < 1 или а > 1, то равенство ar = as справедливо тогда и только тогда, когда r = s.
.
Если а > 1, то
a) неравенство ax > 1 справедливо ⟺ x > 0;
б) неравенство ax < 1 справедливо ⟺ x < 0.
Если а > 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) > h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) < h(x).
Если 0 < а < 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) < h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) > h(x).
Слайд 18
Показательные уравнения
Уравнения вида af(x) = аh(х), где а ≠ 1, a
> 0
называют показательными уравнениями
называют показательными уравнениями
af(x) = аh(х)
f(x) = h(х)
⟺
Методы решения показательных уравнений:
Функционально-графический метод.
Метод уравнивания показателей.
Метод введения новой переменной.
Слайд 28
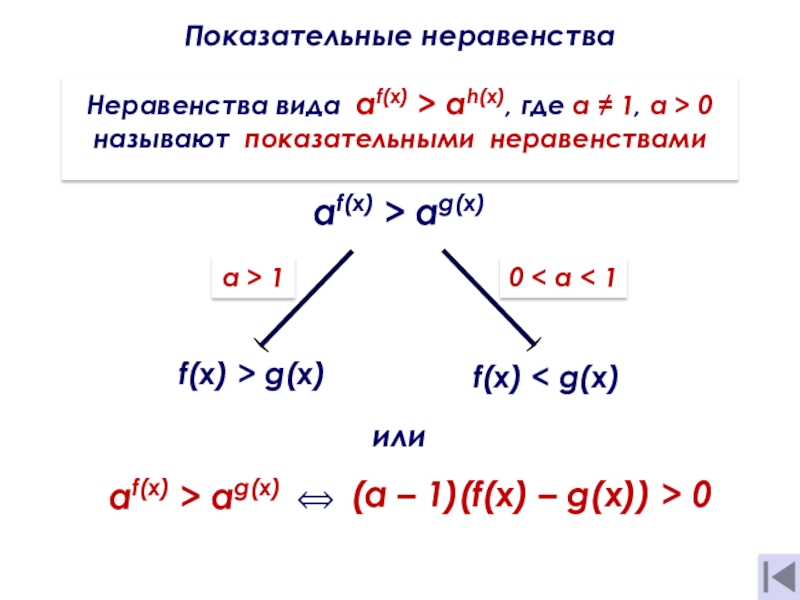
Показательные неравенства
Неравенства вида af(x) > аh(х), где а ≠ 1, a
> 0
называют показательными неравенствами
называют показательными неравенствами
af(x) > аg(х)
f(x) > g(х)
f(x) < g(х)
0 < а < 1
а > 1
af(x) > аg(х) ⟺
(а – 1)(f(x) – g(x)) > 0
или
