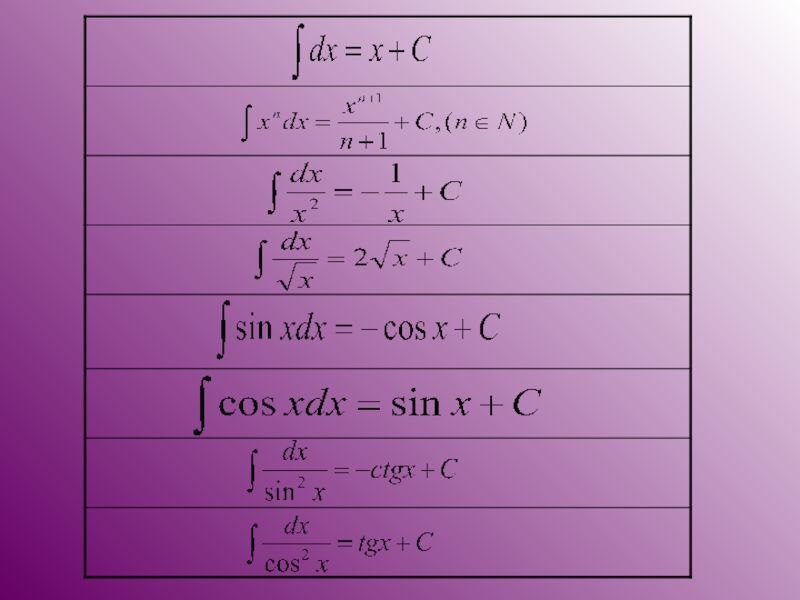- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Первообразная(11 класс)
Содержание
- 1. Презентация по алгебре Первообразная(11 класс)
- 2. Пример: Найти закон движения.V=gttНайдем: S ( t
- 3. (gt² + 5)' =gt + 0 =gt(gt² - 7)' =gt + 0 =gt
- 4. Процесс отыскания производной по заданной функции
- 5. Примеры: 1) y = f (x) =
- 6. Слайд 6
- 7. Правила отыскания первообразных.
- 8. Правило 1. Первообразная суммы равна сумме первообразных.Если
- 9. Правило 2. Постоянный множитель можно вынести за
- 10. Пример 4. Найти первообразную для заданных функций:
- 11. Если функция у = f (x) имеет
- 12. Слайд 12
- 13. Правило 1. Интеграл от суммы функций равен
- 14. Пример: Найти неопределенный интеграл.Решение: По первому и
Слайд 2
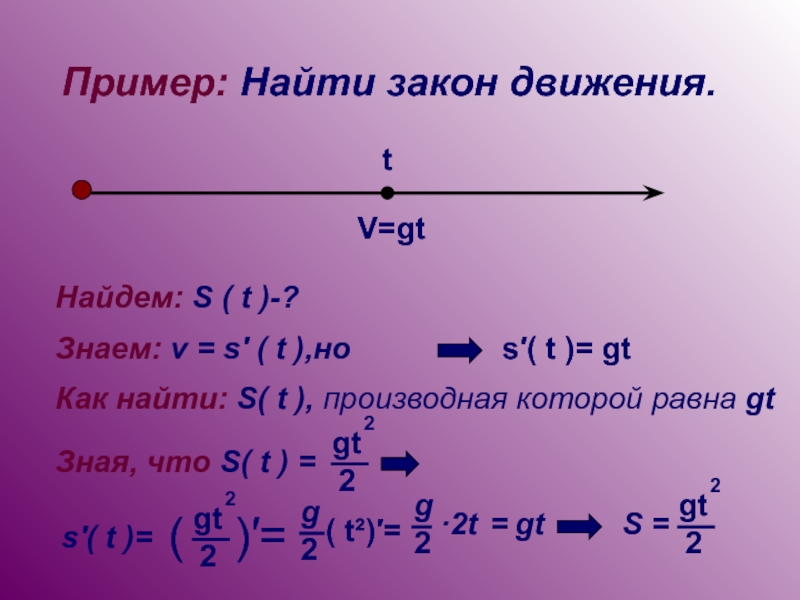
Пример: Найти закон движения.
V=gt
t
Найдем: S ( t )-?
Знаем: v = s'
s′( t )= gt
Как найти: S( t ), производная которой равна gt
s′( t )=
gt
Слайд 4 Процесс отыскания производной по заданной функции называется дифференцированием, а обратную
Саму функцию, которую находят по производной, называют первообразной ( первичный образ)
Функцию у = F(х) называют первообразной для функции у= f(х) на заданном промежутке Х, если для всех х из Х выполняется равенство F‘(х)= f (x)
Слайд 5Примеры:
1) y = f (x) = 2x
первообразная
F (x)
т. к (x²)' = 2x
2) y = f (x) = 3x²
первообразная
F (x) = x³
т. к (x³)' = 3x²
3) y = f (x) = cos x
первообразная
F (x) = sin x
т. к ( sin x)' = cos x
первообразная
Слайд 8Правило 1. Первообразная суммы равна сумме первообразных.
Если функции у = f
Пример: Найти первообразную для функции
y = 2x + cos x
Решение:
Первообразная 2х равна х²
Первообразная соs x равна sin x
первообразная функции У = x² + sin x
Слайд 9Правило 2. Постоянный множитель можно вынести за знак первообразной
Пример 3. Найти
а) у = 5 sin x
Решение:
Первообразная sin x равна – cos x
Первообразная функции равна У = - 5 cos x
Первообразная cos x равна sin x
Слайд 10Пример 4. Найти первообразную для заданных функций:
у = sin
Решение:
Первообразная sin x равна - сos x
Слайд 11Если функция у = f (x) имеет на промежутке Х первообразную
∫f (x)dx
( читают: неопределенный интеграл эф от икс дэ икс)
Слайд 13Правило 1. Интеграл от суммы функций равен сумме интегралов этих функций:
Правило 2. Постоянный множитель можно вынести за знак интеграла:
∫ kf(x)dx = k∫ f(x)dx
Слайд 14Пример: Найти неопределенный интеграл.
Решение: По первому и второму правилу
По 3-й и
В итоге получаем: