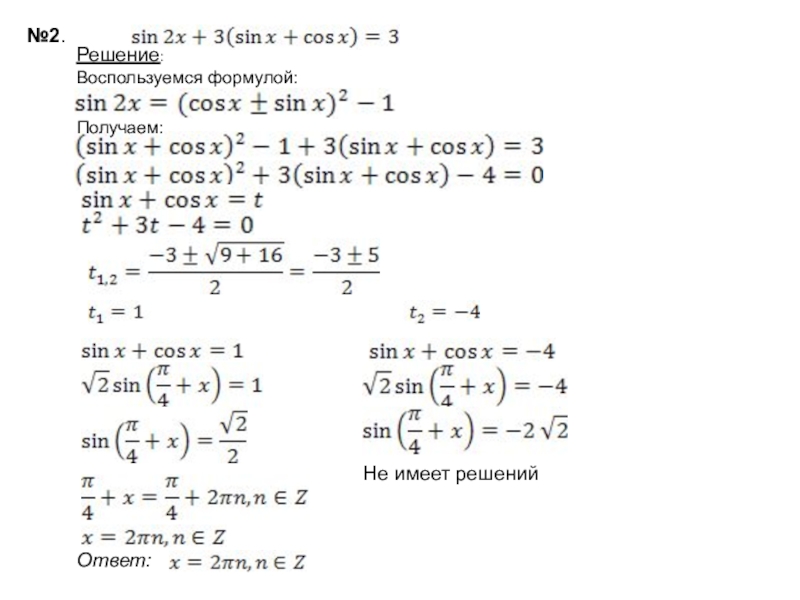- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Основные методы решений тригонометрических уравнений, 10 класс
Содержание
- 1. Презентация по алгебре Основные методы решений тригонометрических уравнений, 10 класс
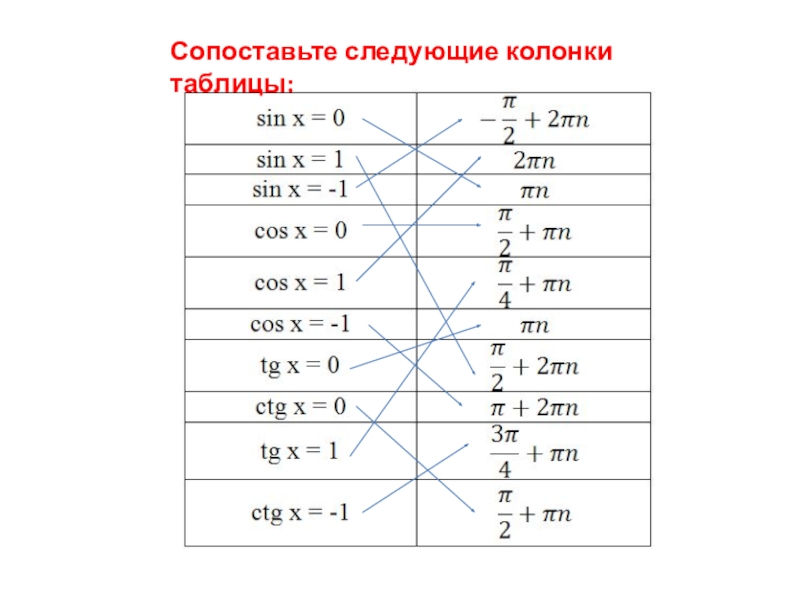
- 2. Сопоставьте следующие колонки таблицы:
- 3. Решить уравнения:1). Решение:Ответ:2). Решение: Ответ:
- 4. 3)ООУ: Решение: Ответ:
- 5. Метод введения вспомогательной переменной. №1. Решение:Замена:Не имеет решенийОтвет:
- 6. №2.Решение: Не имеет решенийОтвет: Воспользуемся формулой:Получаем:
- 7. Метод разложения на множители.№3.Решение:О.О.У.: Данное решение не
- 8. № 4 Решение:Воспользуемся формулой разности косинусов:Не имеет решений Ответ:
- 9. Однородные уравнения.№5 Решение:данная система не имеет решенийСледовательно,
- 10. № 6 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2Решение:3sin 2 x + 4 sin x · cos x +
- 11. Неоднородные уравнения.№ 7 Решение:Поделим обе части уравнения
- 12. Решение:Поделим обе части уравнения наПолучим уравнениеЗамечаем, что
- 13. № 8 Решение:Разделим обе части уравнения
Сопоставьте следующие колонки таблицы:
Слайд 7Метод разложения на множители.
№3.
Решение:
О.О.У.:
Данное решение не удовлетворяет О.О.У.
Ответ:
.
Сгруппируем слагаемые
и вынесем общие множители за скобки:
Слайд 9Однородные уравнения.
№5
Решение:
данная система не имеет решений
Следовательно, cos x = 0
не является корнем данного уравнения и обе части уравнения можно поделить на cos x, т.к. при этом не произойдёт потери корней.
Получим уравнение
Ответ:
- однородное уравнение 1-ой степени
Пусть
Тогда и sin x = 0, получим систему:
Разделим обе части уравнения на, Это можно сделать, т.к.
Слайд 10№ 6 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2
Решение:
3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2 sin 2 x + 2
cos 2 x
Переносим все члены уравнения в одну часть:
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0
Переносим все члены уравнения в одну часть:
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0
данная система не имеет решений
Следовательно, cos x = 0 не является корнем данного уравнения и обе части уравнения можно поделить на cos 2 x, так как при этом не произойдет потеря корней.
Получим уравнение
tg2x + 4tg x + 3 = 0
Делаем замену tg x = t
t5 + 4t + 3 = 0
t1 = -1, t2 = -3
tg x = -1
tg x = -3
Ответ:
Разделим обе части уравнения на cos2x 0.
Слайд 11Неоднородные уравнения.
№ 7
Решение:
Поделим обе части уравнения на
Получим уравнение
Замечаем, что
,
т.е. имеем уравнение
Применяем формулу синуса разности:
Ответ:
Слайд 12
Решение:
Поделим обе части уравнения на
Получим уравнение
Замечаем, что
, т.е. имеем уравнение:
В
данном случае синус и косинус имеют нетабличные значения, поэтому получается очень некрасивое уравнение. Тогда для решения этого уравнения лучше воспользоваться следующим способом.
Слайд 13№ 8
Решение:
Разделим обе части уравнения на
т.к. в этом случае не
произойдет потери корней.
произойдет потери корней.
Ответ:
