- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на темуКомбинаторика
Содержание
- 1. Презентация по алгебре на темуКомбинаторика
- 2. Слайд 2
- 3. Слайд 3
- 4. Правило произведенияПри выборе элемента А из n
- 5. Задача №1. В коробке корзине
- 6. Задача №3. Сколько двузначных чисел можно
- 7. Правило суммыЕсли А можно выбрать n раз,
- 8. Сочетания с повторениями и без
- 9. ПримерыЗадача №6.В коробке находится 4 разных фрукта.
- 10. Размещения с повторениями и без
- 11. Задача №8. Из 3 цифр надо выбрать
- 12. Перестановки с повторениями и без
- 13. ПримерыЗадача №10. Сколько возможных пятизначных чисел можно
- 14. Спасибо за внимание!
Слайд 4Правило произведения
При выборе элемента А из n способов и выборе элемента
Слайд 5 Задача №1. В коробке корзине 2 яблока и 6
Примеры
Слайд 6 Задача №3. Сколько двузначных чисел можно составить из 2 цифр?
Ответ: 2! = 2.
Задача №4. Сколько десятизначных чисел можно составить из 10 цифр?
Ответ: 10! = 3628800.
Примеры
Слайд 7Правило суммы
Если А можно выбрать n раз, а В — m
Задача №5.
В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?
Ответ: 5 + 3 + 7 + 9 = 24.
Слайд 9Примеры
Задача №6.
В коробке находится 4 разных фрукта. Сколькими способами можно достать
Решение:
, где 4! – комбинация из 4 элементов.
С повторениями чуть сложней, комбинации считаются по такой формуле:
Задача №7.
Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.
В этом случае:
Слайд 11Задача №8.
Из 3 цифр надо выбрать 2, чтобы получались разные
Ответ:
Примеры
А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз!
В таком случае общая формула будет выглядеть следующим образом:
Задача №9.
Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.
Решение:
Слайд 13Примеры
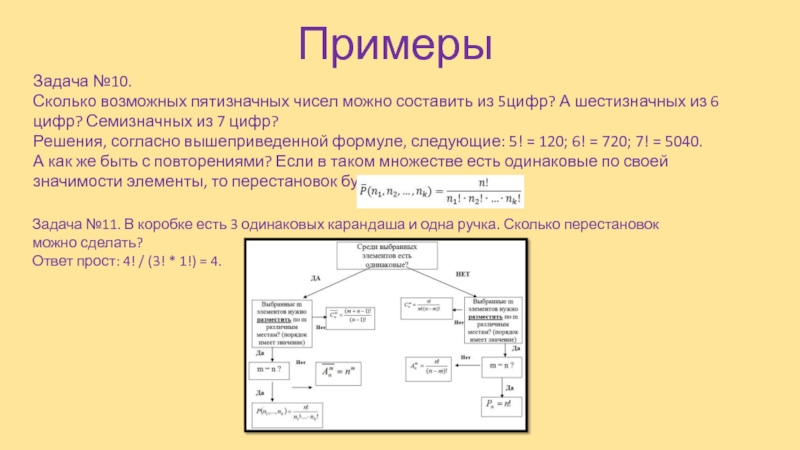
Задача №10.
Сколько возможных пятизначных чисел можно составить из 5цифр? А
Решения, согласно вышеприведенной формуле, следующие: 5! = 120; 6! = 720; 7! = 5040.
А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!
Задача №11. В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?
Ответ прост: 4! / (3! * 1!) = 4.