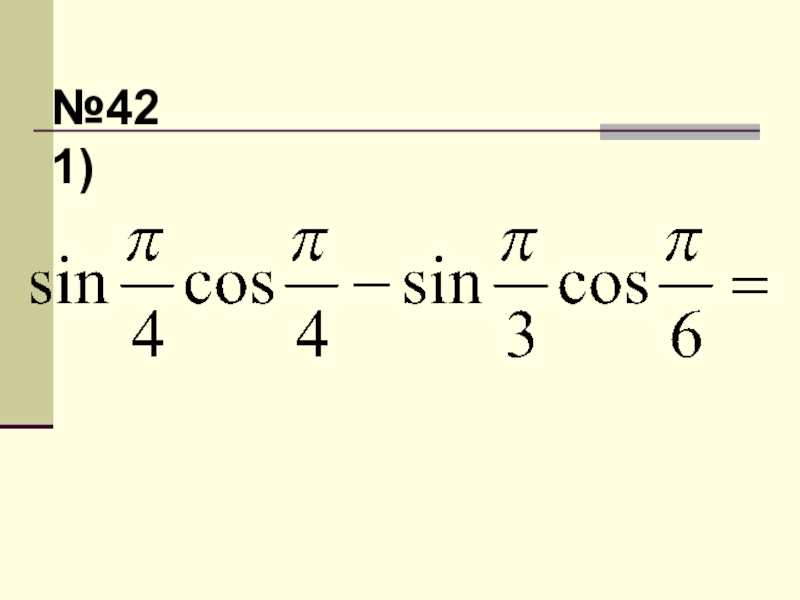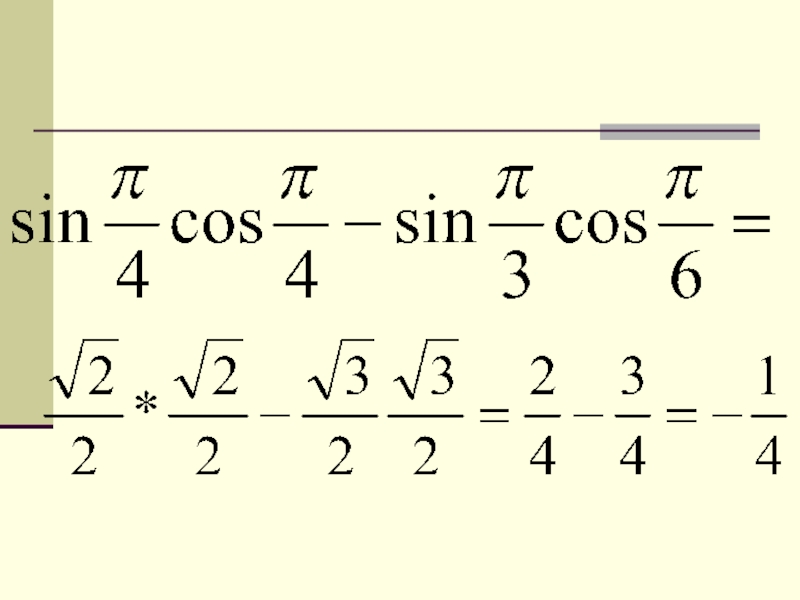с января 1988 года, окончила математический факультет Тюменского государственного университета в 1987 году. Педагогический стаж – 23 года.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Знаки синуса, косинуса, тангенса и котангенса.
Содержание
- 1. Презентация по алгебре на тему Знаки синуса, косинуса, тангенса и котангенса.
- 2. Презентация к уроку по теме:Знаки синуса, косинуса, тангенса и котангенса.
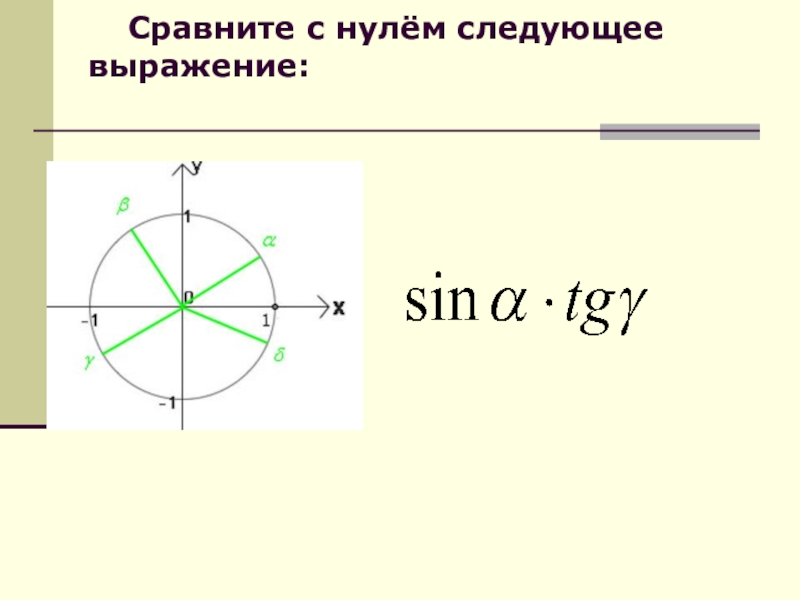
- 3. Мы изучаем
- 4. Математика есть такая наука, которая показывает, как
- 5. Щетков Максим подготовил презентацию по теме: ИСТОРИЯ ТРИГОНОМЕТРИИ И УЧЁНЫЕ ЕЁ СОЗДАВШИЕ
- 6. Выполните самостоятельно
- 7. Индивидуальное задание:
- 8. Слайд 8
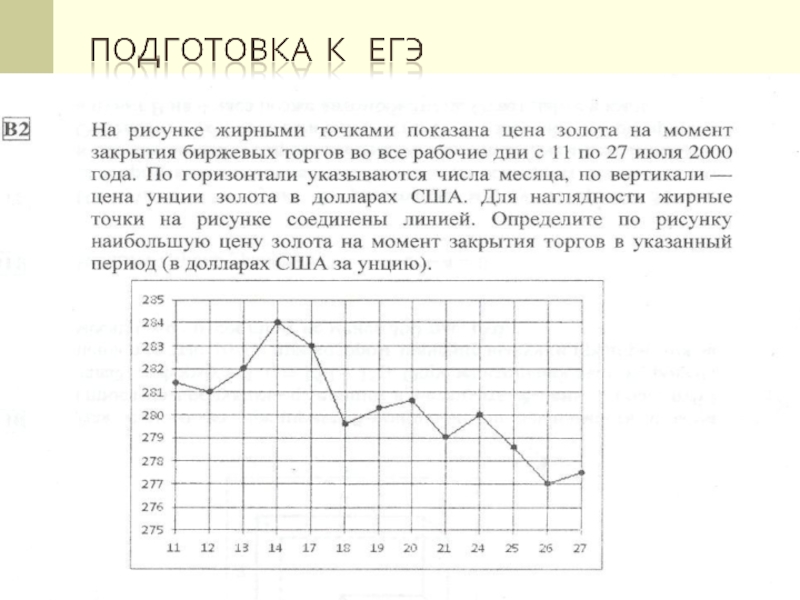
- 9. Ответ: 284
- 10. Слайд 10
- 11. Решение:1) 700х 0,4 = 280 руб2) 190
- 12. В12. В сосуд, содержащий 2 кг 80%-го
- 13. 1) 2 кг – 100 %
- 14. Разминка по теме (устно)Назовите формулу перехода от градусной меры угла к радианной.
- 15. Формула перехода от градусной меры угла к радианной:
- 16. Выразить угол в радианах с помощью
- 17. Выразить угол в радианах с помощью
- 18. Назовите формулу перехода от радианной меры угла к градусной .
- 19. Формула перехода от радианной меры угла к градусной :
- 20. Найдите градусную меру угла, радианная мера которого равна:
- 21. Найдите градусную меру угла, радианная мера которого равна:
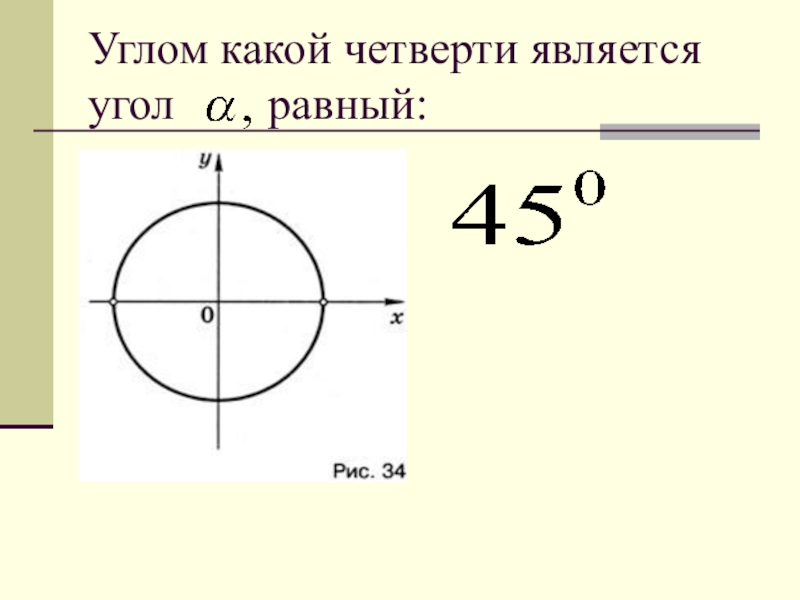
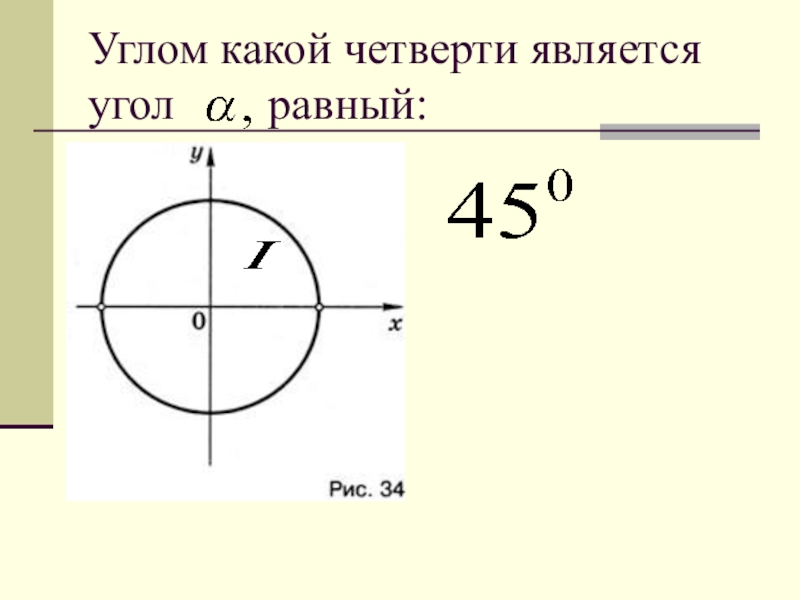
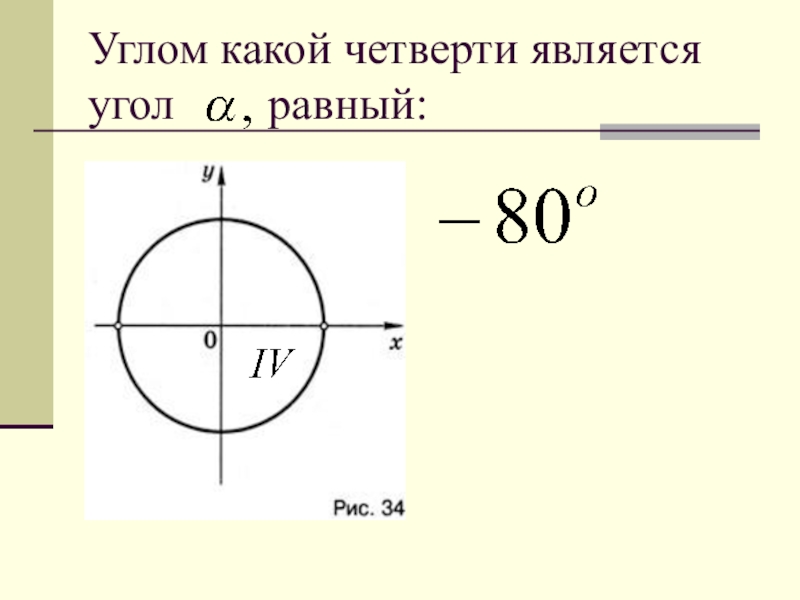
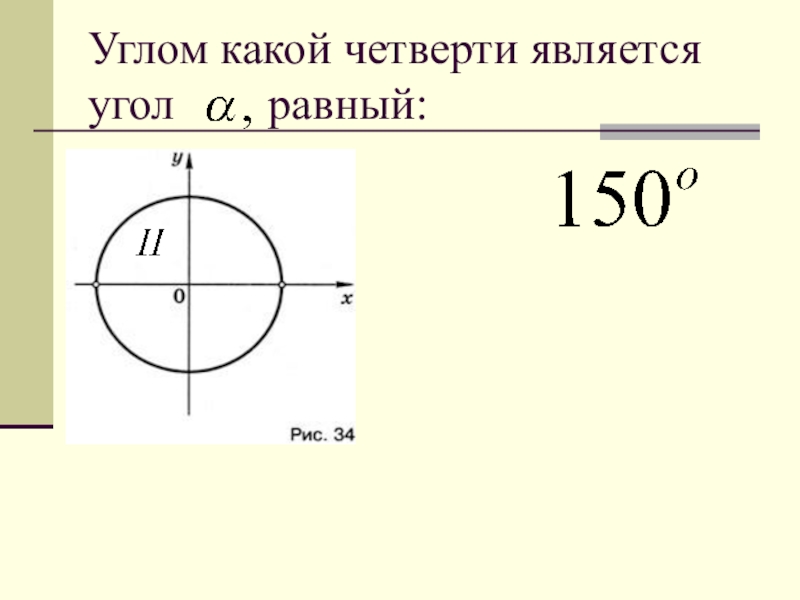
- 22. Углом какой четверти является угол равный:
- 23. Углом какой четверти является угол равный:
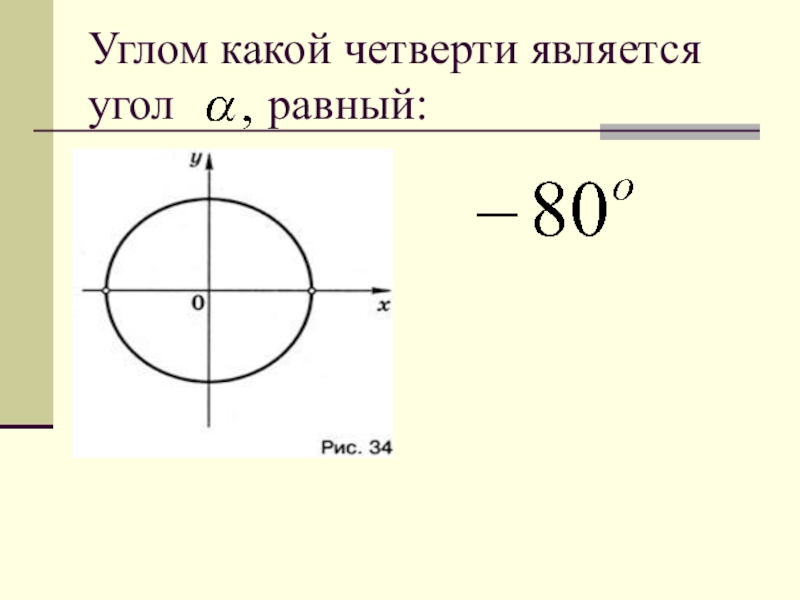
- 24. Углом какой четверти является угол равный:
- 25. Углом какой четверти является угол равный:
- 26. Углом какой четверти является угол равный:
- 27. Углом какой четверти является угол равный:
- 28. Сформулируйте определение синуса, косинуса, тангенса, котангенса угла а.
- 29. Вычислить:sin=
- 30. Вычислить:sin=
- 31. Вычислить: cos=
- 32. Вычислить: cos=
- 33. Вычислить: tg=
- 34. Вычислить: tg=
- 35. Вычислить: cos=
- 36. Вычислить: cos=1
- 37. №421)
- 38. Слайд 38
- 39. Сравните с нулём следующее выражение:
- 40. ТЕМА УРОКА:
- 41. Тема урока Знаки синуса, косинуса, тангенса и котангенса.
- 42. Выясните, в какой четверти находится точка, полученная
- 43. Решение:1) II ч< α
- 44. Выясните, в какой четверти находится точка, полученная
- 45. Решение:2) III ч< α
- 46. Выясните, в какой четверти находится точка, полученная
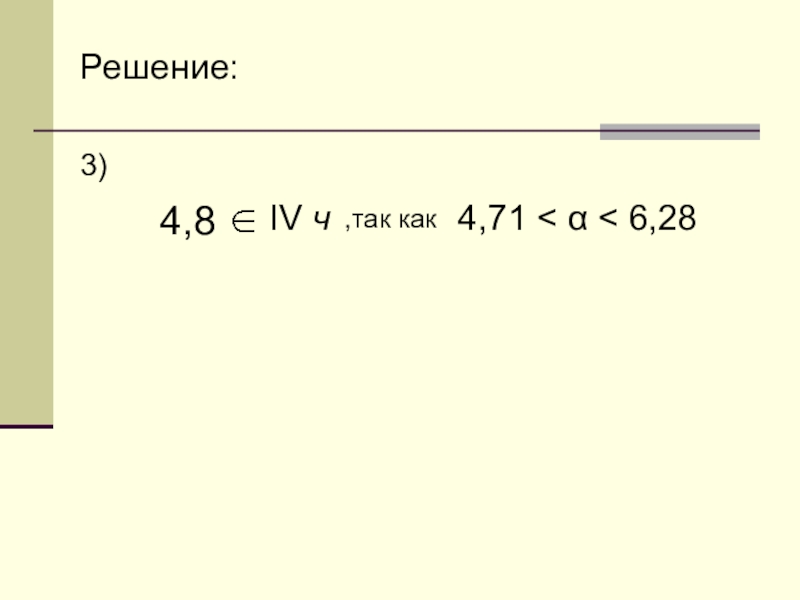
- 47. Решение:3) 4,8 4,71 < α < 6,28IV ч,так как
- 48. Точка Р(1;0) движется по единичной окружности против
- 49. Изучение новой темы: Если для точек, находящихся в
- 50. Какие знаки имеют ординаты и абсциссы для точек, находящихся во второй четверти.
- 51. < α < Если для точек,
- 52. Какие знаки имеют ординаты и абсциссы для точек, находящихся в третьей четверти.
- 53. Если для точек, расположенных в третьей четверти,
- 54. Какие знаки имеют ординаты и абсциссы для точек, находящихся в четвертой четверти.
- 55. < α < Если для точек, расположенных
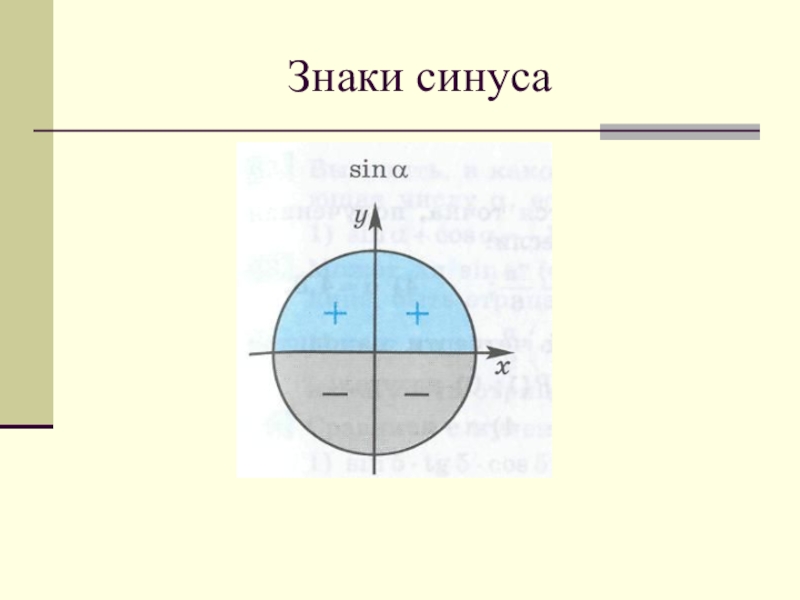
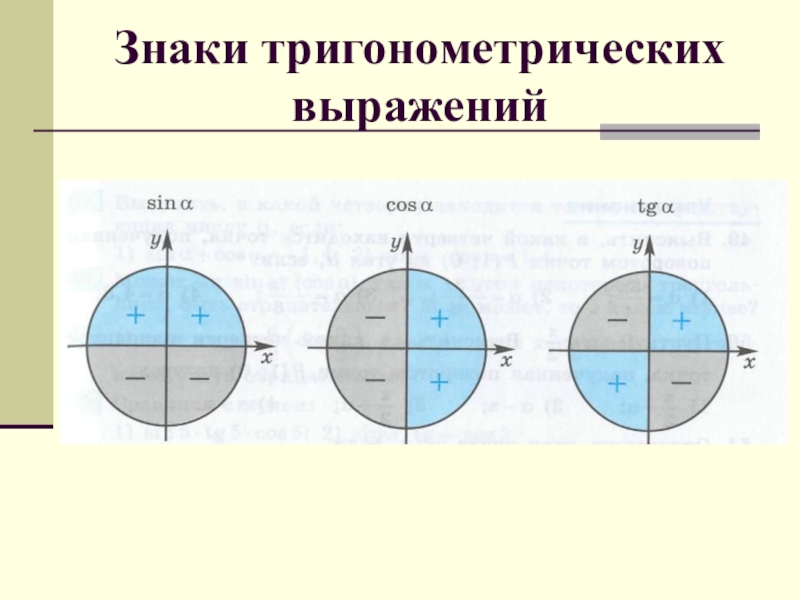
- 56. Знаки синуса
- 57. Знаки синуса
- 58. Знаки косинуса
- 59. Знаки косинуса
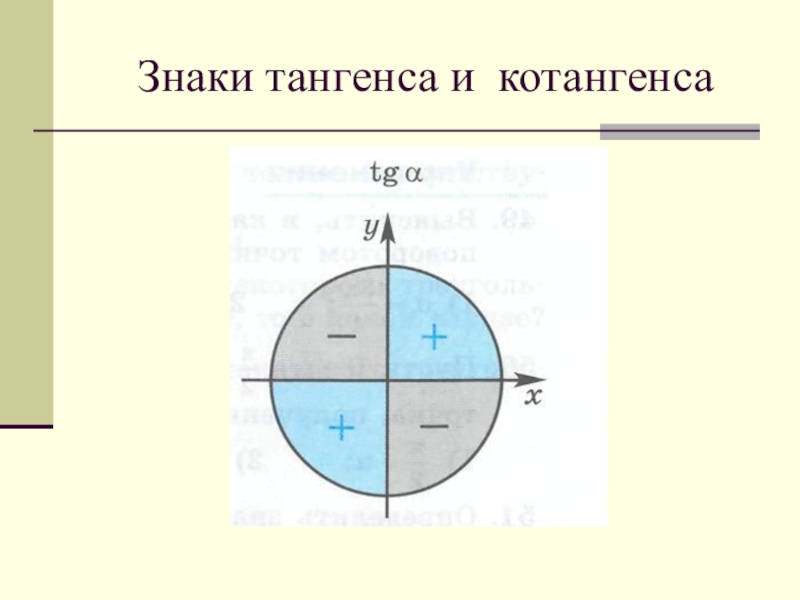
- 60. Знаки тангенса и котангенса
- 61. Знаки тангенса и котангенса
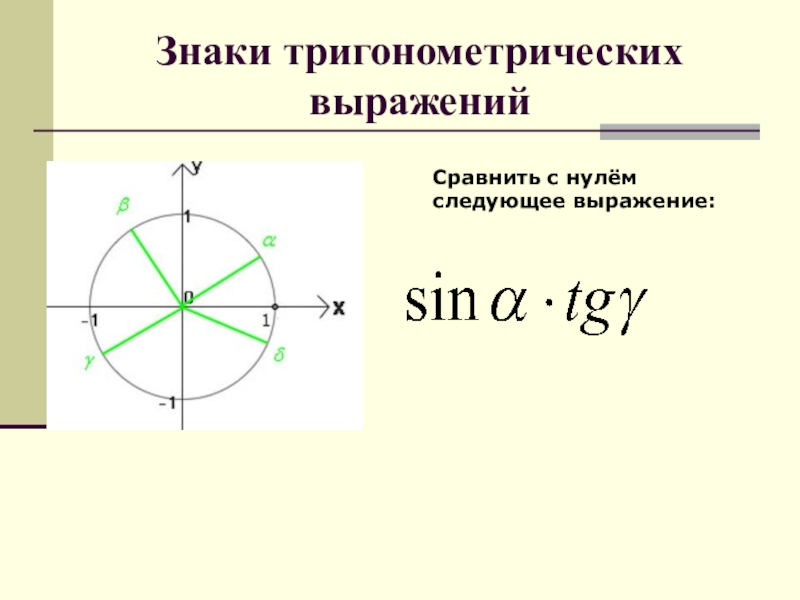
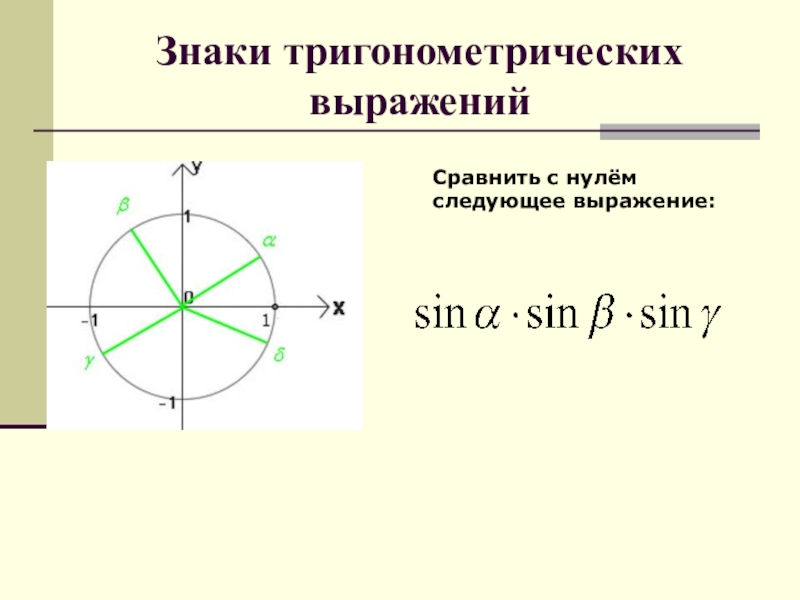
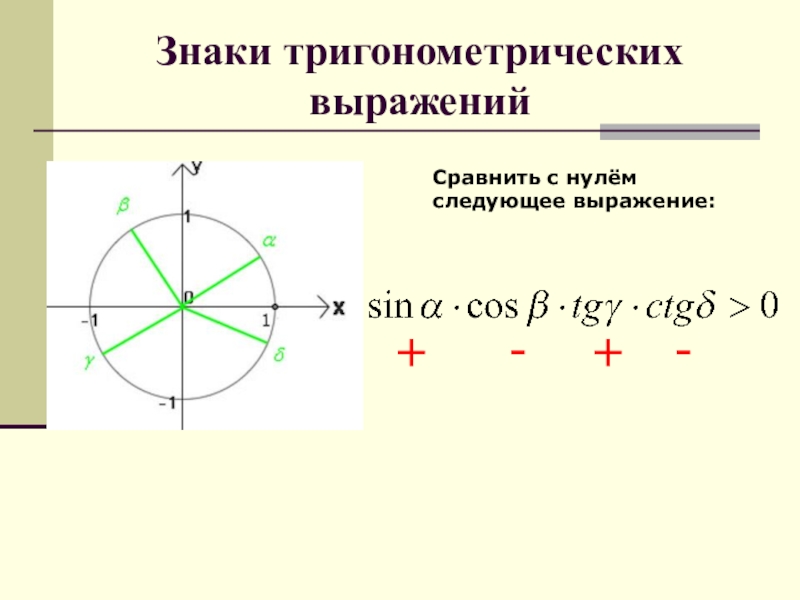
- 62. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:
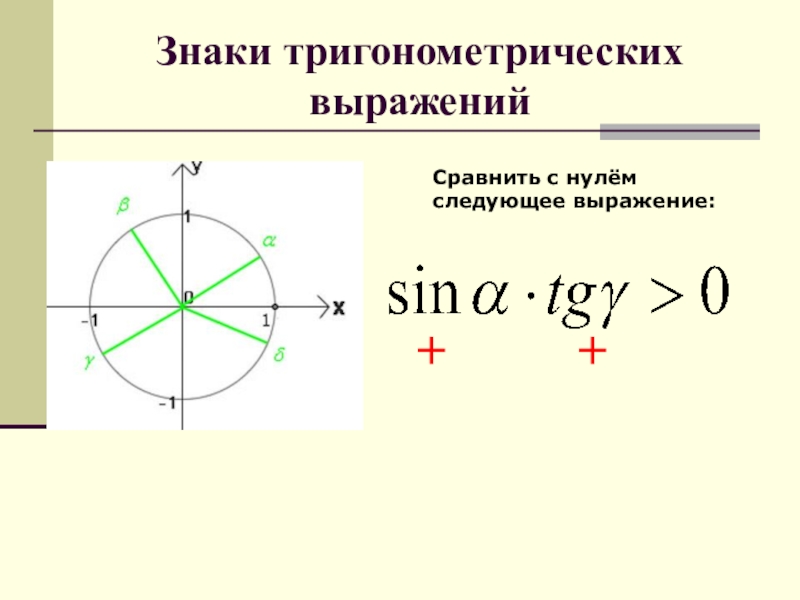
- 63. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:+ +
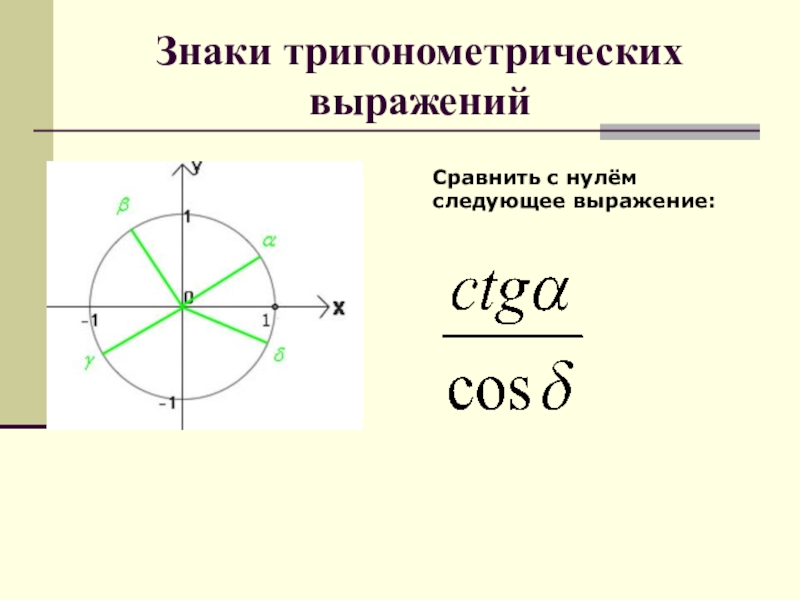
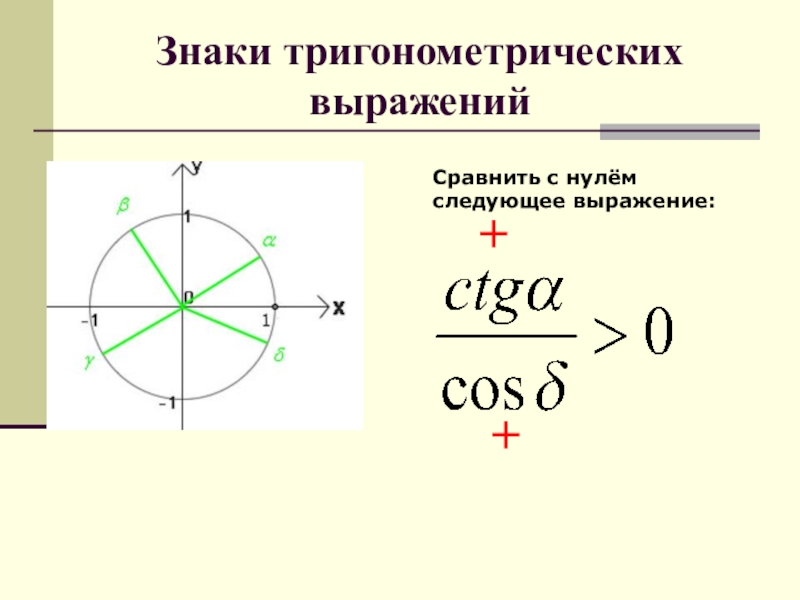
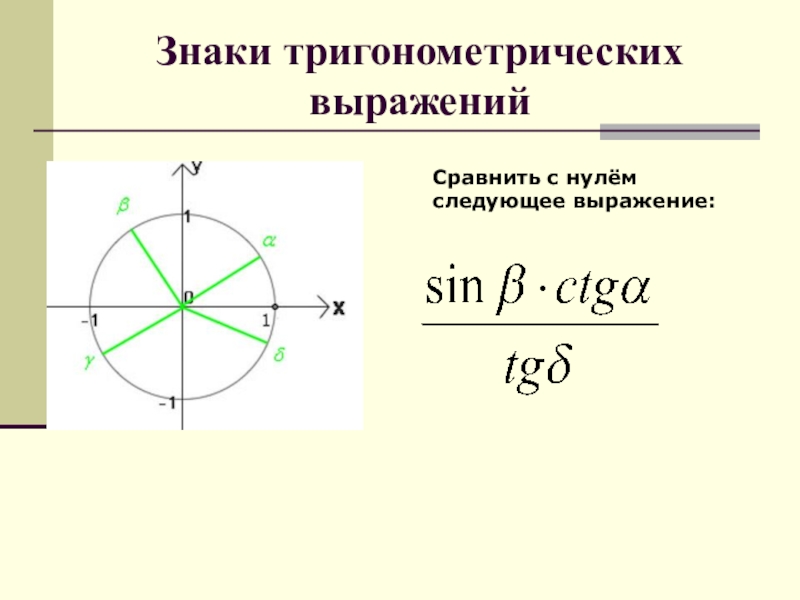
- 64. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:
- 65. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:++
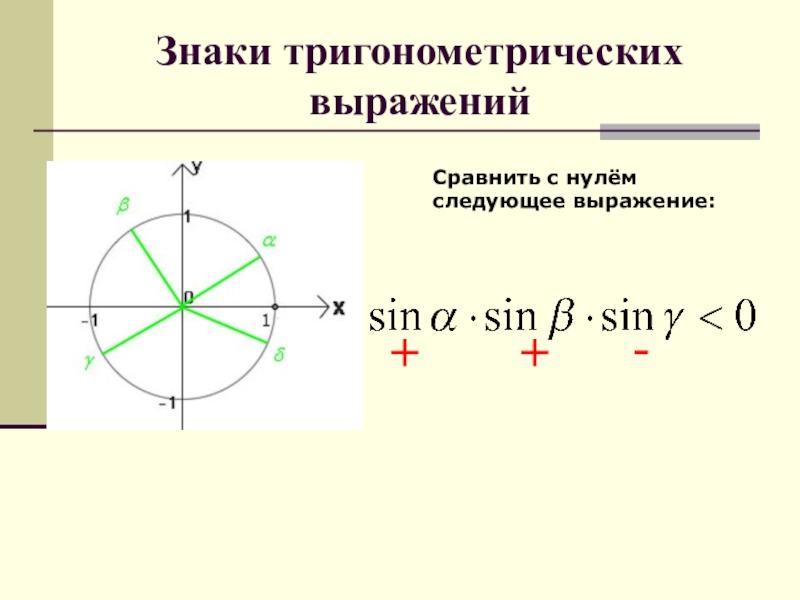
- 66. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:
- 67. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:+ + -
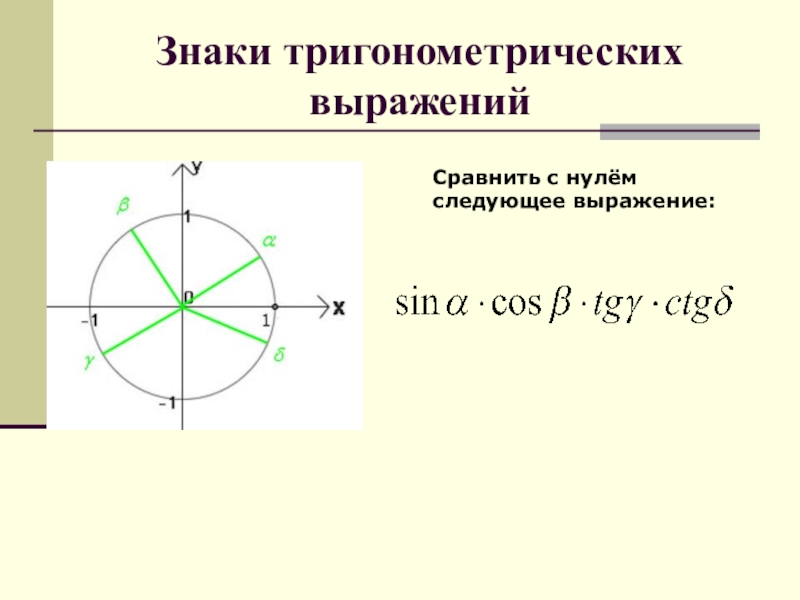
- 68. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:
- 69. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:+ - + -
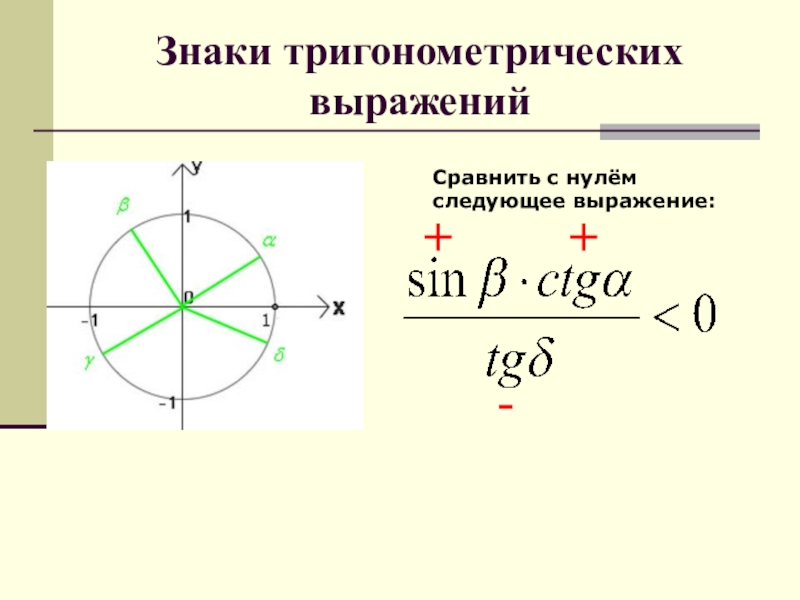
- 70. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:
- 71. Знаки тригонометрических выраженийСравнить с нулём следующее выражение:+ +-
- 72. № 55 (2). Определить знаки чисел sina, cosa, tga если: α = 3.
- 73. № 55 2) Так как α = 3, π /2 < 3 < π , где (π ≈ 3,14)
- 74. № 55 2) Так как α = 3, π /2
- 75. № 55 2) Так как α = 3, π /2 0, cos 3
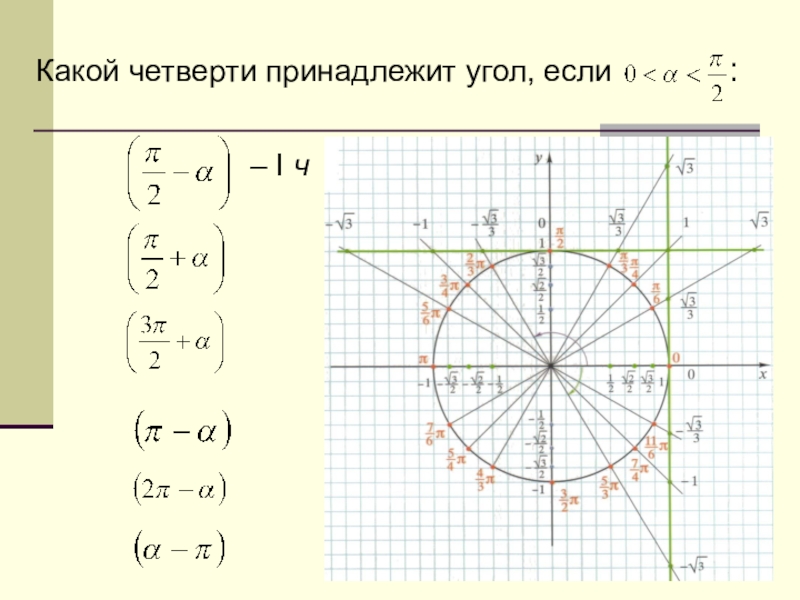
- 76. Какой четверти принадлежит угол, если
- 77. Какой четверти принадлежит угол, если : – I ч
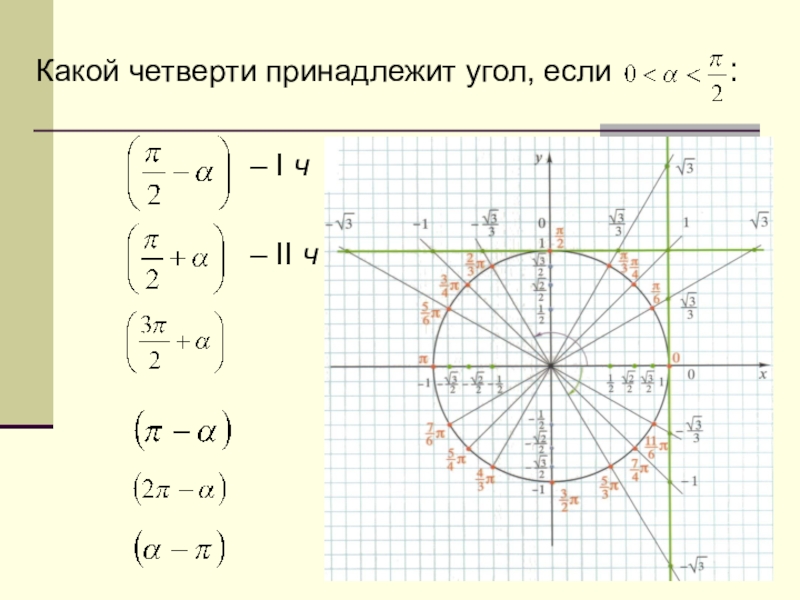
- 78. Какой четверти принадлежит угол, если
- 79. Какой четверти принадлежит угол, если : 1)
- 80. № 56 Определить знак числа, если
- 81. № 56 Определить знак числа, если
- 82. № 56 Определить знак числа, если
- 83. № 56 Определить знак числа, если
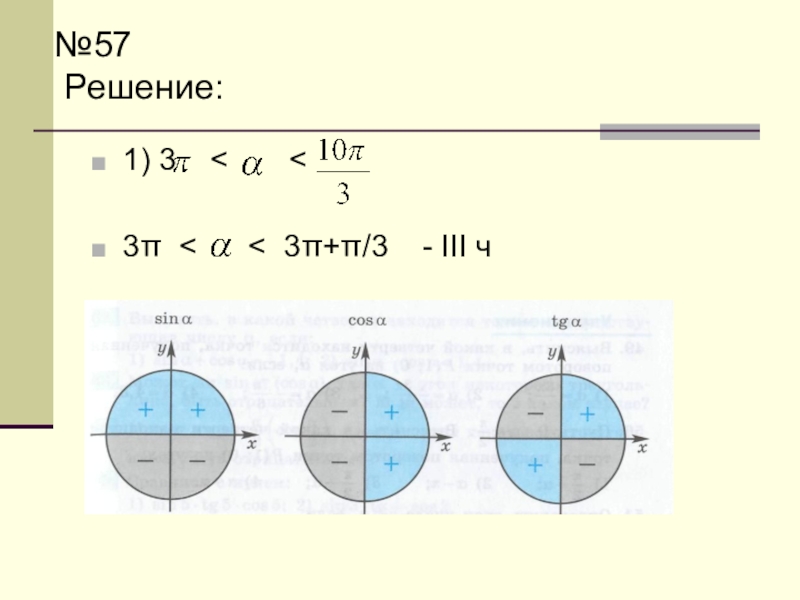
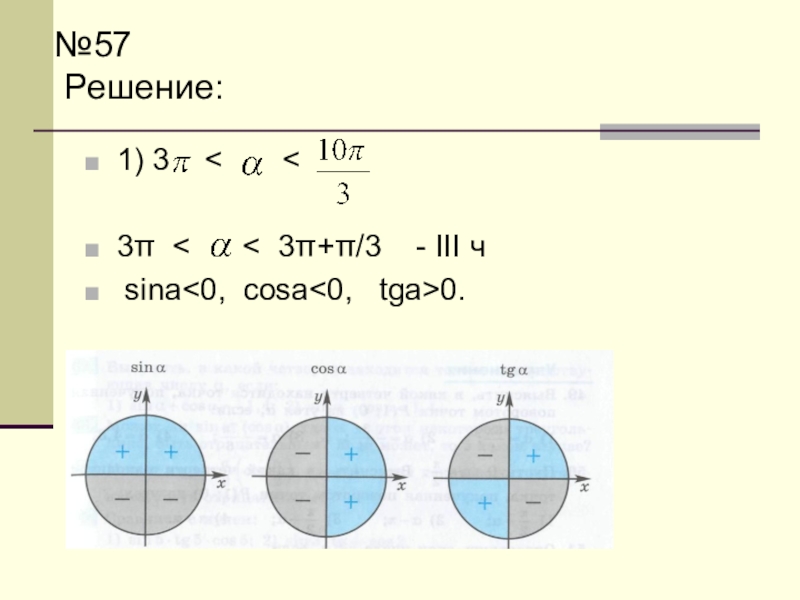
- 84. №57 Выясните, каковы знаки чисел sina,
- 85. №57 Решение: 1) 3
- 86. №57 Решение: 1) 3
- 87. №57 Решение: 1) 3
- 88. № 61 Решить уравнениеsin(5π+х)=1
- 89. № 61 Решить уравнениеsin(5π+х)=1 5π+х = π/2+2 πк, к Z
- 90. № 61 Решить уравнениеsin(5π+х)=1 5π+х = π/2+2
- 91. № 61 Решить уравнениеsin(5π+х)=1 5π+х = π/2+2
- 92. № 61 Решить уравнениеsin(5π+х)=1 5π+х = π/2+2
- 93. Знаки тригонометрических выражений
- 94. Знаки тригонометрических выражений
Презентация к уроку по теме:Знаки синуса, косинуса, тангенса и котангенса.
Слайд 4
Математика есть такая наука, которая показывает, как из знаемых количеств находить
другие, нам еще неизвестные.
Д.С. Аничков
Д.С. Аничков
Слайд 11Решение:
1) 700х 0,4 = 280 руб
2) 190 + 280х0,3 = 190+84
= 274 руб– наиболее дешевый тарифный план
3) 325 руб
Ответ: 274
3) 325 руб
Ответ: 274
Слайд 12
В12. В сосуд, содержащий 2 кг 80%-го водного раствора уксуса, добавили
3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.
Слайд 131) 2 кг – 100 %
х кг
– 80 %
Х= 2х80/100 = 1,6 (кг)- уксусной кислоты
2) 2+3=5 кг – 100 %
1,6 кг – х %
Х= 1,6х100/5 = 32 % – всего раствора
Ответ: 32
Х= 2х80/100 = 1,6 (кг)- уксусной кислоты
2) 2+3=5 кг – 100 %
1,6 кг – х %
Х= 1,6х100/5 = 32 % – всего раствора
Ответ: 32
Слайд 42 Выясните, в какой четверти находится точка, полученная поворотом точки Р(1;0) на
угол α, если (устно):
1)
α =
Слайд 44 Выясните, в какой четверти находится точка, полученная поворотом точки Р(1;0) на
угол α, если:
2)
–
α =
Слайд 46 Выясните, в какой четверти находится точка, полученная поворотом точки Р(1;0) на
угол α, если:
3)
α = 4,8 рад
Слайд 48
Точка Р(1;0) движется по единичной окружности против часовой стрелки. Какие знаки
имеют ординаты и абсциссы для точек, находящихся в первой четверти.
Слайд 49Изучение новой темы:
Если для точек, находящихся в первой четверти, ординаты и
абсциссы положительны, то какие знаки принимают значения синуса, косинуса, тангенса и котангенса угла α, где
Слайд 51< α <
Если для точек, расположенных во второй четверти, ординаты
положительны а абсциссы отрицательны, то какие знаки принимают значения синуса, косинуса, тангенса и котангенса угла α, где
Слайд 53 Если для точек, расположенных в третьей четверти, ординаты и абсциссы отрицательны,
то какие знаки принимают значения синуса, косинуса, тангенса и котангенса угла α, где
< α <
Слайд 55< α <
Если для точек, расположенных в четвертой четверти, ординаты отрицательны,
а абсциссы положительны, то какие знаки принимают значения синуса, косинуса, тангенса и котангенса угла α, где
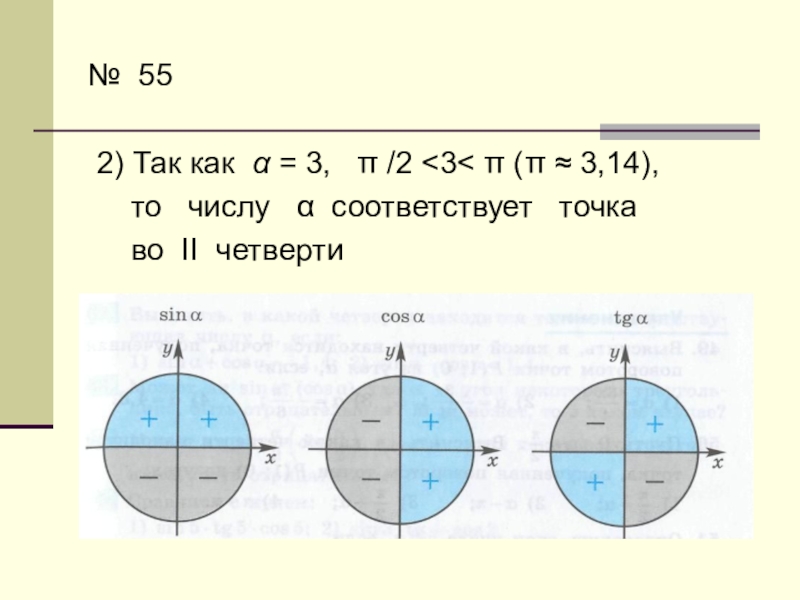
Слайд 75№ 55
2) Так как α = 3, π /2
то числу α соответствует точка
во II четверти, поэтому
sin 3 > 0,
cos 3 < 0,
tg 3 < 0.
во II четверти, поэтому
sin 3 > 0,
cos 3 < 0,
tg 3 < 0.
Слайд 79Какой четверти принадлежит угол, если :
1)
2)
3)
4)
5)
6)
– I ч
– II ч
– IV ч
– II ч
– IV ч
– III ч
Слайд 91№ 61 Решить уравнение
sin(5π+х)=1
5π+х = π/2+2 πк, к Z
х = π/2– 5π+2 πк, к Z
х = (π–10π)/2+2 πк, к Z
х = (π–10π)/2+2 πк, к Z
Слайд 92№ 61 Решить уравнение
sin(5π+х)=1
5π+х = π/2+2 πк, к Z
х = π/2– 5π+2 πк, к Z
х = (π–10π)/2+2 πк, к Z
х = –9π/2+2 πк, к Z
Ответ: х = –9π/2+2 πк, к Z
х = (π–10π)/2+2 πк, к Z
х = –9π/2+2 πк, к Z
Ответ: х = –9π/2+2 πк, к Z
