- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Уравнения касательной
Содержание
- 1. Презентация по алгебре на тему Уравнения касательной
- 2. ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(Х)
- 3. УРАВНЕНИЕ ВИДА У=F(A)+F’(A)(Х-А) ЯВЛЯЕТСЯ УРАВНЕНИЕМ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ.
- 4. АЛГОРИТМ СОСТАВЛЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(X)Обозначить
- 5. УСЛОВИЯ ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПРЯМЫХ.Пусть
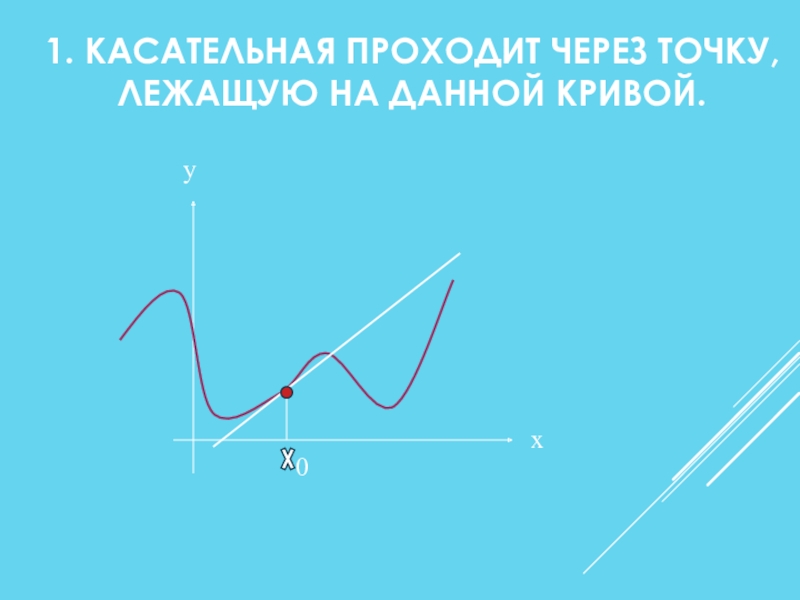
- 6. 1. КАСАТЕЛЬНАЯ ПРОХОДИТ ЧЕРЕЗ ТОЧКУ, ЛЕЖАЩУЮ НА ДАННОЙ КРИВОЙ.0ху
- 7. Даны дифференцируемая функция у=f(х) и 1) абсцисса
- 8. РЕШЕНИЕ ТАКИХ ЗАДАЧ СВОДИТСЯ:к последовательному отысканию f(a)
- 9. Составьте уравнение касательной к графику функции у=х2–2х–3
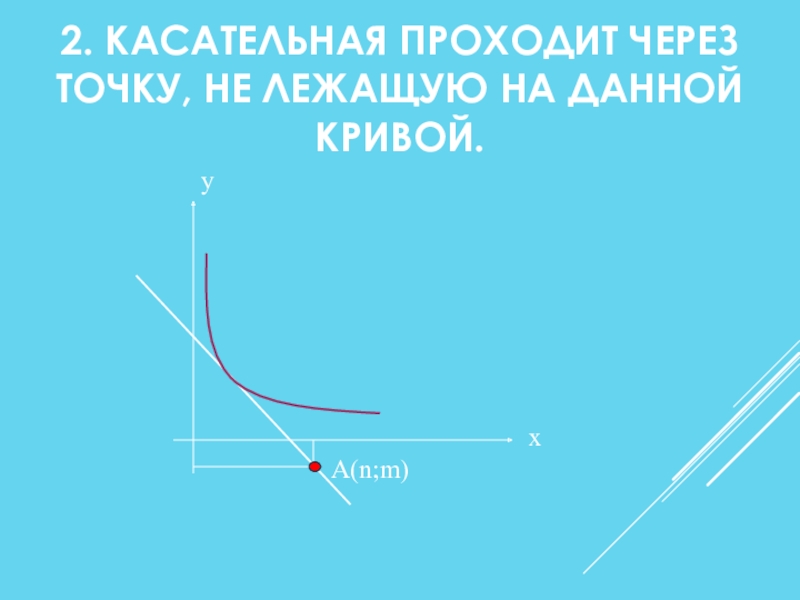
- 10. 2. КАСАТЕЛЬНАЯ ПРОХОДИТ ЧЕРЕЗ ТОЧКУ, НЕ ЛЕЖАЩУЮ
- 11. Даны дифференцируемая функция у=f(х) и 1) точка
- 12. РЕШЕНИЕ ТАКИХ ЗАДАЧ ОСНОВЫВАЕТСЯ НА ТОМ, ЧТО
- 13. Напишите уравнение всех касательных к графику функции
- 14. 3. КАСАТЕЛЬНАЯ ПРОХОДИТ ПОД НЕКОТОРЫМ УГЛОМ К
- 15. Даны дифференцируемая функция у=f(х) и 1) значение
- 16. РЕШАЯ УРАВНЕНИЕ F’(A)=K ИЛИ F’(A)=TGΑ (ЕСЛИ ЗАДАН УГОЛ Α) НАХОДИМ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ А.
- 17. Напишите уравнения всех касательных к графику функции
- 18. 4. КАСАТЕЛЬНАЯ ЯВЛЯЕТСЯ ОБЩЕЙ ДЛЯ ДВУХ КРИВЫХ.
- 19. Даны дифференцируемые функция у=f(х) и y=g(x). Нужно найти уравнения общих касательных к графику этих функций.
- 20. 1 способ. Такие задачи
- 21. 2 способ.1) Находим уравнение касательной к графику
- 22. Напишите уравнения всех общих касательных к графикам
- 23. ЯВЛЯЕТСЯ ЛИ ДАННАЯ ПРЯМАЯ КАСАТЕЛЬНОЙ К ГРАФИКУ
- 24. 1 способ. Если у=kх+b –
- 25. 2 способ. Прямая у=kх+b является
ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(Х) Пусть дана некоторая кривая и точка Р на ней. Возьмем на этой кривой другую точку Р1 и проведем прямую через точки Р и Р1. Эту прямую называют
Слайд 2ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(Х)
Пусть дана
некоторая кривая и точка Р на ней. Возьмем на этой кривой другую точку Р1 и проведем прямую через точки Р и Р1. Эту прямую называют секущей. Будем приближать точку Р1 к Р. Положение секущей РР1 будет меняться (стремиться к точки Р) предельное положение прямой РР1 и будет касательной к кривой в точке Р.
Слайд 4АЛГОРИТМ СОСТАВЛЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(X)
Обозначить буквой а абсциссу точки
касания.
Найти f(а).
Найти f’(x) и f’(а).
Подставить найденные числа а, f(а), f’(а) в общее уравнение касательной у=f(a)+f’(a)(x-a)
Найти f(а).
Найти f’(x) и f’(а).
Подставить найденные числа а, f(а), f’(а) в общее уравнение касательной у=f(a)+f’(a)(x-a)
Слайд 5 УСЛОВИЯ ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПРЯМЫХ.
Пусть даны две прямые: у1=k1x+b1
и у2=k2x+b2.
Если k1= k2, то прямая у1 параллельна у2.
Если k1⋅k2=–1, то данные прямые взаимно перпендикулярны.
Если k1= k2, то прямая у1 параллельна у2.
Если k1⋅k2=–1, то данные прямые взаимно перпендикулярны.
Слайд 7Даны дифференцируемая функция у=f(х) и
1) абсцисса точки касания;
2)
ордината точки касания;
3) абсцисса точки касания задана как пересечение двух графиков функций;
4) абсцисса точки касания задана как корень данного уравнения.
3) абсцисса точки касания задана как пересечение двух графиков функций;
4) абсцисса точки касания задана как корень данного уравнения.
Слайд 8РЕШЕНИЕ ТАКИХ ЗАДАЧ СВОДИТСЯ:
к последовательному отысканию f(a) и f’(a);
решая уравнение f(a)=у0,
находим а;
находим точки пересечения двух графиков; решая уравнение f(x)=g(x);
находим корень данного уравнения.
находим точки пересечения двух графиков; решая уравнение f(x)=g(x);
находим корень данного уравнения.
Слайд 9Составьте уравнение касательной к графику функции у=х2–2х–3 в точке с абсциссой
х0=2.
Решение. 1. Обозначим абсциссу точки касания а, тогда а=2.
2. Найдем f(a): f(a)=22–2·2–3, f(a)=-3.
3. Найдем f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2.
4. Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x–a): у=-3+2(х–2),
у=-3+2х–4, у=2х–7 – уравнение касательной.
Ответ: у=2х –7.
Решение. 1. Обозначим абсциссу точки касания а, тогда а=2.
2. Найдем f(a): f(a)=22–2·2–3, f(a)=-3.
3. Найдем f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2.
4. Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x–a): у=-3+2(х–2),
у=-3+2х–4, у=2х–7 – уравнение касательной.
Ответ: у=2х –7.
Слайд 11Даны дифференцируемая функция у=f(х) и
1) точка А(n;m) через которую
проходит касательная;
2) точка А(n;m) задана как пересечение двух графиков функций;
3) точка А(n;m) задана как корень системы уравнений.
2) точка А(n;m) задана как пересечение двух графиков функций;
3) точка А(n;m) задана как корень системы уравнений.
Слайд 12РЕШЕНИЕ ТАКИХ ЗАДАЧ ОСНОВЫВАЕТСЯ НА ТОМ, ЧТО КООРДИНАТЫ ТОЧКИ А(N;M) ДОЛЖНЫ
УДОВЛЕТВОРЯТЬ ИСКОМОМУ УРАВНЕНИЮ КАСАТЕЛЬНОЙ:
решая уравнение m=f(a)+f’(a)(m-a) найдем а и, таким образом, приходим к задаче первого типа;
находим точки пересечения двух графиков, решая уравнения f(x)=g(x) и у=g(х) или у=f(x);
находим корень данной системы уравнений.
Слайд 13Напишите уравнение всех касательных к графику функции
у = х2
+4х+6 проходящих через точку М(-3;-1).
Решение. 1. Точка М(-3;-1) не является точкой касания, так как f(-3)=3.
2. а – абсцисса точки касания.
3. Найдем f(a): f(a) = a 2+4a+6.
4. Найдем f’(x) и f’(a): f’(x)=2x+4, f’(a)=2a+4.
5. Подставим числа а, f(a), в общее уравнение касательной
у= f(a)+ f’(a)(x–a): y=a2+4a+6+(2a+4)(x–a) – уравнение касательной.
Так как касательная проходит через точку М(-3;-1), то -1=a2+4a+6+(2a+4)(-3–a), a2+6a+5=0, a=-5 или a=-1.
Если a=-5, то y=-6x–19 – уравнение касательной.
Если a=-1, y=2x+5 – уравнение касательной.
Ответ: y=-6x–19, y=2x+5.
Решение. 1. Точка М(-3;-1) не является точкой касания, так как f(-3)=3.
2. а – абсцисса точки касания.
3. Найдем f(a): f(a) = a 2+4a+6.
4. Найдем f’(x) и f’(a): f’(x)=2x+4, f’(a)=2a+4.
5. Подставим числа а, f(a), в общее уравнение касательной
у= f(a)+ f’(a)(x–a): y=a2+4a+6+(2a+4)(x–a) – уравнение касательной.
Так как касательная проходит через точку М(-3;-1), то -1=a2+4a+6+(2a+4)(-3–a), a2+6a+5=0, a=-5 или a=-1.
Если a=-5, то y=-6x–19 – уравнение касательной.
Если a=-1, y=2x+5 – уравнение касательной.
Ответ: y=-6x–19, y=2x+5.
Слайд 15Даны дифференцируемая функция у=f(х) и
1) значение производной в точке
касания f’(а);
2) указан угловой коэффициент касательной;
3) задан угол, между касательной к графику функции и данной прямой.
2) указан угловой коэффициент касательной;
3) задан угол, между касательной к графику функции и данной прямой.
Слайд 17Напишите уравнения всех касательных к графику функции у=х2–2х–8, параллельных прямой у=-4х–4.
Решение.
1. Обозначим абсциссу точки касания а.
2. Найдем f(a): f(a)=a2–2a–8.
3. Найдем f’(x) и f’(a): f’(x)=2x–2, f’(a)=2a–2.
Но, с другой стороны, f’(a)= - 4 (условие параллельности). Решив уравнение 2a–2= - 4, получим a= - 1, f(a)= - 5.
Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x-a): y=-5–4(x+1),
y= - 4x–9 – уравнение касательной.
Ответ: y= - 4x–9.
2. Найдем f(a): f(a)=a2–2a–8.
3. Найдем f’(x) и f’(a): f’(x)=2x–2, f’(a)=2a–2.
Но, с другой стороны, f’(a)= - 4 (условие параллельности). Решив уравнение 2a–2= - 4, получим a= - 1, f(a)= - 5.
Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x-a): y=-5–4(x+1),
y= - 4x–9 – уравнение касательной.
Ответ: y= - 4x–9.
Слайд 19Даны дифференцируемые функция у=f(х) и y=g(x). Нужно найти уравнения общих касательных
к графику этих функций.
Слайд 20 1 способ.
Такие задачи можно решать с помощью
необходимого и достаточного признака того, что прямая у=kх+b является касательной к графику функции у=f(х) и у=g(х). Тогда задача сводится к решению системы:
f(m)=km+b,
g(n)=kn+b,
f’(m)=k,
g’(n)=k,
где (m;f(m)) и (n;g(n)) – точки касания искомой прямой с графиками функций у=f(х) и у=g(х) соответственно. Решив систему, получим возможные значения k и b и запишем уравнения общих касательных в виде у=kх+b.
f(m)=km+b,
g(n)=kn+b,
f’(m)=k,
g’(n)=k,
где (m;f(m)) и (n;g(n)) – точки касания искомой прямой с графиками функций у=f(х) и у=g(х) соответственно. Решив систему, получим возможные значения k и b и запишем уравнения общих касательных в виде у=kх+b.
Слайд 212 способ.
1) Находим уравнение касательной к графику функции у=f(х) в точке
с абсциссой а.
2) Находим уравнение касательной к графику функции у=g(х) в точке с абсциссой а.
3) Полученные прямые должны совпадать, т. е. решаем систему:
k1=k2,
b1=b2.
2) Находим уравнение касательной к графику функции у=g(х) в точке с абсциссой а.
3) Полученные прямые должны совпадать, т. е. решаем систему:
k1=k2,
b1=b2.
Слайд 22Напишите уравнения всех общих касательных к графикам функций у=х2+х+1 и. у=0,5(х2+3).
Решение.
I 1. а – абсцисса точки касания графика функции у=х2+х+1
2. Найдем f(a): f(a) =a2+а+1.
3. Найдем f’(x) и f’(a): f’(x)=2x+1, f”(a)=2a+1.
4. Подставим а, f(a), в общее уравнение касательной
у=f(a)+ f’(a)(x–a): y=a2+а+1+(2a+1)⋅(x–a), y=(2a+1)x–a2+1 – уравнение касательной.
II. 1. с – абсцисса точки касания графика функции у=0,5(х2 +3).
2. Найдем f(c): f(c)=0,5c2 +1,5.
3. Найдем f’(x) и f’(c): f’(x)=х, f’(c)=c.
4. Подставим а, f(a), в общее уравнение касательной у=f(a)+ f’(a)(x–a):
y=0,5c2+1,5+c(x–c), y=cx–0,5c2+1,5 – уравнение касательной.
Так как касательная общая, то 2a+1=c, c=1, с=-3
–a2+1= –0,5c2+1,5 a=0; или а=-2
Итак, y=x+1 и y=-3x–3 общие касательные.
Ответ: y=x+1 и y=–3x–3.
2. Найдем f(a): f(a) =a2+а+1.
3. Найдем f’(x) и f’(a): f’(x)=2x+1, f”(a)=2a+1.
4. Подставим а, f(a), в общее уравнение касательной
у=f(a)+ f’(a)(x–a): y=a2+а+1+(2a+1)⋅(x–a), y=(2a+1)x–a2+1 – уравнение касательной.
II. 1. с – абсцисса точки касания графика функции у=0,5(х2 +3).
2. Найдем f(c): f(c)=0,5c2 +1,5.
3. Найдем f’(x) и f’(c): f’(x)=х, f’(c)=c.
4. Подставим а, f(a), в общее уравнение касательной у=f(a)+ f’(a)(x–a):
y=0,5c2+1,5+c(x–c), y=cx–0,5c2+1,5 – уравнение касательной.
Так как касательная общая, то 2a+1=c, c=1, с=-3
–a2+1= –0,5c2+1,5 a=0; или а=-2
Итак, y=x+1 и y=-3x–3 общие касательные.
Ответ: y=x+1 и y=–3x–3.
Слайд 23ЯВЛЯЕТСЯ ЛИ ДАННАЯ ПРЯМАЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=F(X)?
Даны дифференцируемая функция
у=f(х) и уравнение прямой у=kх+b. Выясните, является ли данная прямая касательной к графику функции у=f(x).
Слайд 241 способ.
Если у=kх+b – уравнение к графику функции
в точке с абсциссой а, то f’(а)=k. Решив это уравнение, находим а и задача сводится к решению первого типа задач на касательную. Полученное уравнение сравнивается с данным уравнением прямой.
Слайд 252 способ.
Прямая у=kх+b является касательной к графику функции
у=f(x) в том и только том случае, если существует такое значение а, при котором совпадают значения данных функций и значения их производных, т. е. Совместна система
f(a)=ka+b,
f’(a)=k.
f(a)=ka+b,
f’(a)=k.