- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Уравнения приводимые к квадратным
Содержание
- 1. Презентация по алгебре на тему Уравнения приводимые к квадратным
- 2. Слайд 2
- 3. 1. МАТЕМАТИЧЕСКИЙ МАРАФОНРешите уравнение:
- 4. 2.РАБОТАЕМ УСТНО:Найдите корни уравнений:Назовите степень каждого уравнения.4; 4,50; 1/3-5; 0; 530,25; 1-1; -0,1; 0,1
- 5. Способы решения уравнений высших степеней: 1.
- 6. Рассмотрим решение уравнений высших степеней, используя
- 7. Решить самостоятельноПРИМЕР №2: Решите уравнениеРазложим левую часть уравнения на множители:Ответ: -1; 1/6; 6.
- 8. Рассмотрим решение уравнений высших степеней, используя
- 9. Вариант 1Часть 11. Какое из уравнений имеет
- 10. п. 13 (ст. 81) проработатьВыполнить: 1 гр.
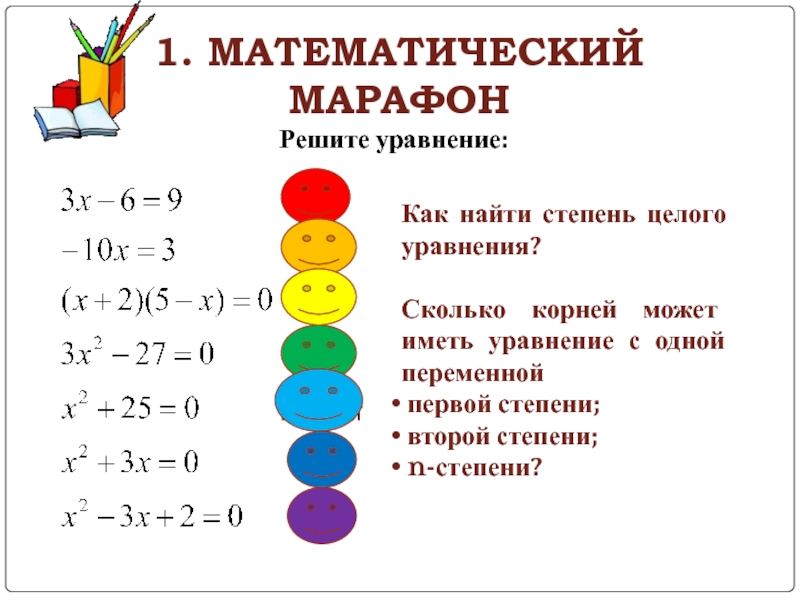
Слайд 31. МАТЕМАТИЧЕСКИЙ МАРАФОН
Решите уравнение:
Х
корней нет
Х = 0; -3
Х = -3; 3
Х = -2; 5
Х = -0,3
Х = 1; 2
Как найти степень целого уравнения?
Сколько корней может иметь уравнение с одной переменной
первой степени;
второй степени;
n-степени?
Слайд 42.РАБОТАЕМ УСТНО:
Найдите корни уравнений:
Назовите степень каждого уравнения.
4; 4,5
0; 1/3
-5; 0; 5
3
0,25;
-1; -0,1; 0,1
Слайд 5Способы решения уравнений высших степеней:
1. Метод разложение на множители.
2. Метод введения
Слайд 6Рассмотрим решение уравнений высших степеней,
используя метод разложение на множители.
ПРИМЕР №1:
Разложим левую часть уравнения на множители:
Когда произведение множителей равно нулю?
Ответ: -1; -0,5; 1.
Слайд 7Решить самостоятельно
ПРИМЕР №2: Решите уравнение
Разложим левую часть уравнения на множители:
Ответ:
Слайд 8Рассмотрим решение уравнений высших степеней,
используя метод введения новой переменной.
ПРИМЕР №3:
Обозначим
2.
y
y
3. Находим переменную x:
Ответ: -3; 2.
Решить уравнение
Приведем к общему знаменателю,
найдем ОДЗ и решим целое уравнение
Слайд 9Вариант 1
Часть 1
1. Какое из уравнений имеет корни, равные – 1;
А. (x – 1)(x2 – 9) = 0 Б. (x + 1)(x2 – 9) = 0 В. (x + 1)(x2 + 9) = 0 Г. (x – 1)(x2 + 9) = 0
2. Найдите корни уравнения (2x – 3)(x + 4) = 0.
А. 1,5 и – 4 Б. – 1,5 и 4 В. 1,5 и 4 Г. – 1,5 и – 4
3. Решите уравнение: 5 x2 = 25x
Ответ:
Часть 2
4. Закончи фразу: «Произведение корней уравнения x4 – 2x2 – 8 = 0 равно числу …»
А. – 8 Б. – 4 В. – 2 Г. 0
5. Решите уравнение ( решение и ответы оформите на отельном листе)
(x2 + 4x)(x2 + 4x – 17) = – 60
Ответ:
Вариант 2
Часть 1
1. Какое из уравнений имеет корни, равные – 2; 5 – 5?
А. (x – 2)(x2 – 25) = 0
Б. (x + 2)( x2 + 25) = 0
В. (x + 2)( x2 – 25) = 0
Г. (x – 2)( x2 + 25) = 0
2. Найдите корни уравнения (2x + 7)(x – 4) = 0.
А. 3,5 и – 4
Б. – 3,5 и – 4
В. 3,5 и 4
Г. – 3,5 и 4
3. Решите уравнение: 3x – x2 = 0
Ответ:_______________________________
Часть 2
4. Закончи фразу: «Произведение корней уравнения x4 – 8x2 – 9 = 0 равно числу …»
А. – 1
Б. – 9
В. 9
Г. – 8
5. Решите уравнение ( решение и ответы оформите на отельном листе)
(x2 – 5x)(x2 – 5x + 10) + 24 = 0
Ответ:
Контрольный тест
-5; 1; 2; 6
0; 5
0; 3
1; 2; 3; 4
Слайд 10п. 13 (ст. 81) проработать
Выполнить:
1 гр. - №294 (б)
2 гр.
Повт. №291 (Б) для 1 и 2 гр.
Домашнее задание