- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Стандартный вид одночлена (7 класс)
Содержание
- 1. Презентация по алгебре на тему Стандартный вид одночлена (7 класс)
- 2. Целые алгебраические выражения – это множества букв
- 3. Выражение, представляющее собой произведение чисел, переменных и их степеней, называется одночленом.Примеры: Одночлены
- 4. называется произведение, составленное из числового множителя (коэффициента)
- 5. Степенью одночлена стандартного вида называется сумма показателей
- 6. Одночлен, который состоит только из коэффициента, не
- 7. Одночлены, отличающиеся только числовым коэффициентом или равные между собой, называются подобными.Пример:Одночлены подобные
- 8. Противоположными одночленами называются те, которые имеют одинаковый коэффициент, но разные знаки:Пример:Одночлены противоположные
- 9. Результатом сложения подобных одночленов является другой одночлен,
- 10. Результатом вычитанием подобных одночленов является другой одночлен,
- 11. При умножении одночленов с одной переменной получается
- 12. При делении одночленов с одной переменной получается
- 13. Результатом возведения в степень является одночлен, чей
- 14. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Понятие одночлена.
Стандартный вид одночлена.
МКОУ «Пахомовская СОШ»
Учитель математики: Кузнецова Н.В.
Слайд 2Целые алгебраические выражения – это множества букв и чисел, смешанных внутри
Целое алгебраическое выражение – это такое выражение, где в знаменателе нет никакой буквы.
В противном случае названное выше алгебраическое выражение называется рациональным
Алгебраические выражения
Слайд 3Выражение, представляющее собой произведение чисел, переменных и их степеней, называется одночленом.
Примеры:
Одночлены
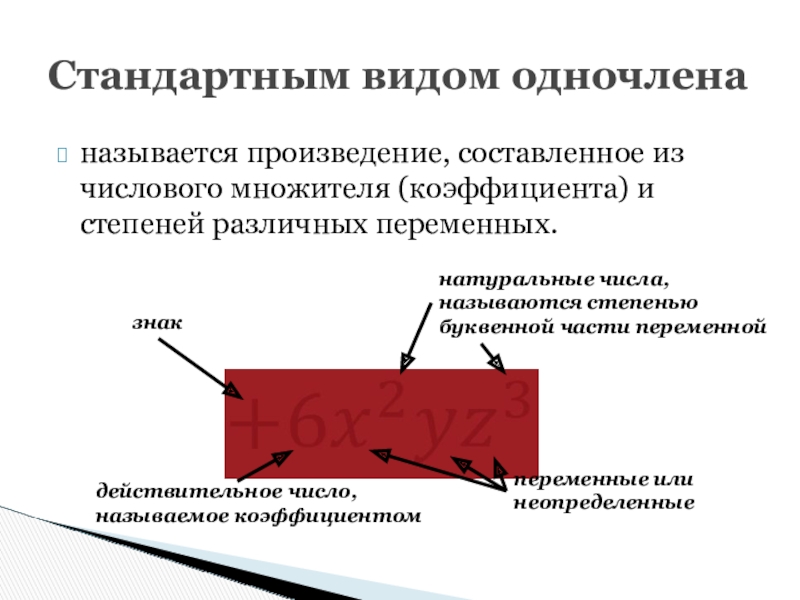
Слайд 4называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных.
Стандартным
знак
натуральные числа,
называются степенью
буквенной части переменной
действительное число,
называемое коэффициентом
переменные или
неопределенные
Слайд 5Степенью одночлена стандартного вида называется сумма показателей степеней переменных.
Пример:
в данном
Степень одночлена
Слайд 6Одночлен, который состоит только из коэффициента, не умноженного ни на какую
Пример: 5; ; ; (так как ; )
Если одночлен имеет степень 1, как , принято опускать показатель степени и писать только букву: 5x.
Частные случаи степени одночлена
Слайд 7Одночлены, отличающиеся только числовым коэффициентом или равные между собой, называются подобными.
Пример:
Одночлены
Слайд 8Противоположными одночленами называются те, которые имеют одинаковый коэффициент, но разные знаки:
Пример:
Одночлены
Слайд 9Результатом сложения подобных одночленов является другой одночлен, который получается при сложении
Сложение одночленов
Слайд 10Результатом вычитанием подобных одночленов является другой одночлен, который получается прибавлением к
Вычитание одночленов
Слайд 11При умножении одночленов с одной переменной получается другой одночлен, коэффициент которого
Произведение одночленов
Слайд 12При делении одночленов с одной переменной получается другой одночлен, коэффициент которого
Деление одночленов
Слайд 13Результатом возведения в степень является одночлен, чей коэффициент равен коэффициенту в
Возведение в степень