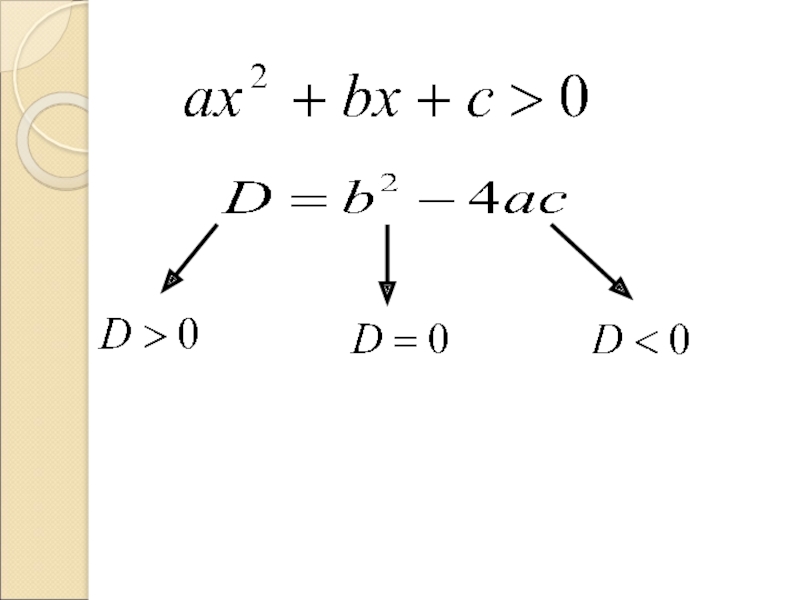учреждение средняя общеобразовательная школа №30 имени А.И.Колдунова
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Решение рациональных неравенств
Содержание
- 1. Презентация по алгебре на тему Решение рациональных неравенств
- 2. Линейные неравенстваНеравенство вида ах+в≥0, где а, в
- 3. Свойства неравенств:1.Из любой части неравенства можно переносить
- 4. 2.Обе части неравенства можно умножить
- 5. 3.Обе части неравенства можно умножить
- 6. Квадратные неравенства Неравенство вида ах²+вх+с
- 7. Чтобы решить квадратное неравенство методом парабол, надо:
- 8. Слайд 8
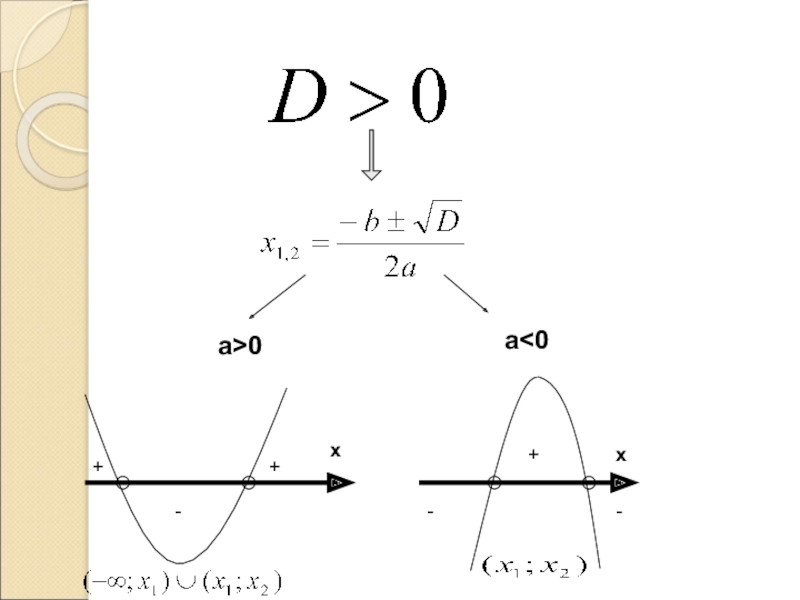
- 9. a>0a
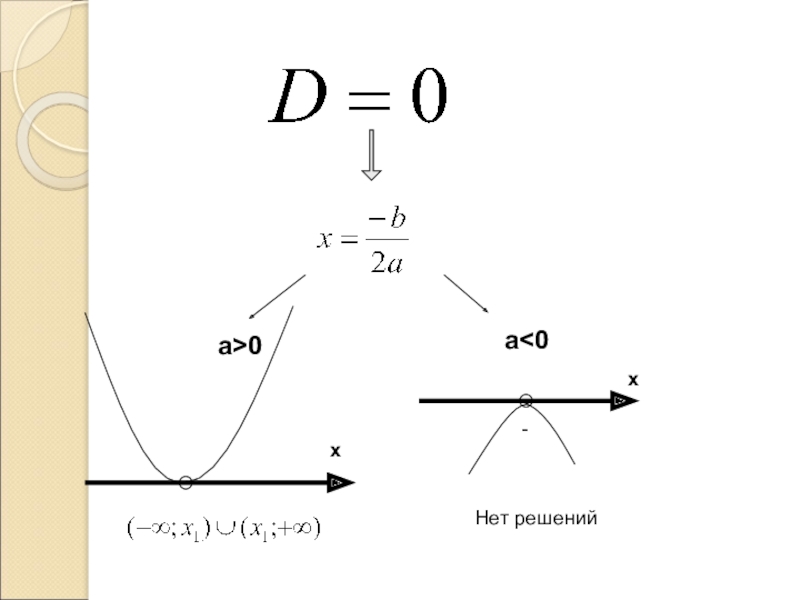
- 10. a>0a
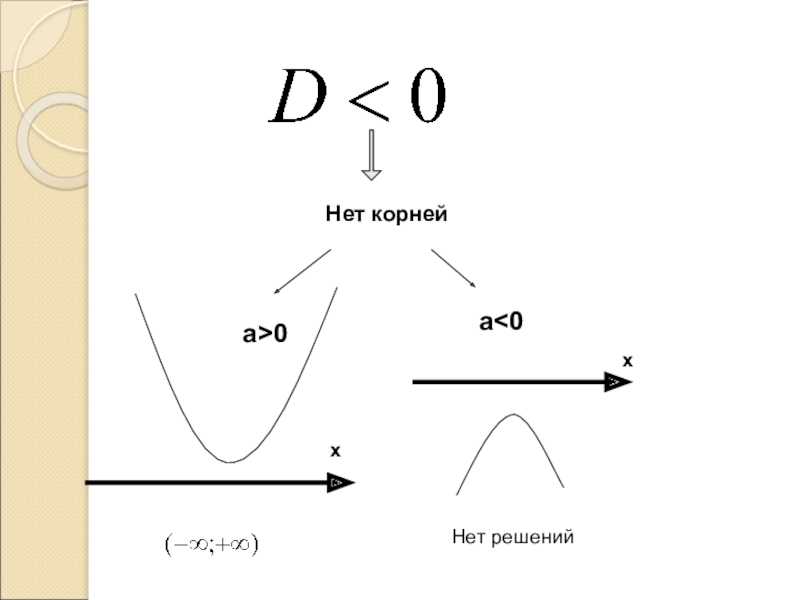
- 11. a>0a
- 12. 1.Решить неравенство: -х²+7х-12≥0 Рассмотрим функцию у=-х²+7х-12 Коэффициент а=-1,значит ветви
- 13. 2.Решим неравенство х²-4>0 у=х²-4, а=1- ветви параболы направлены вверх; х²-4=0 х²=4 х=±2 Строим параболу (схематично)х-22
Линейные неравенстваНеравенство вида ах+в≥0, где а, в - любые числа, а≠0, называется линейным.Например: а) 0,5х≤0 б) -3х>0
Слайд 1Решение рациональных неравенств
9 класс
Подготовила:
учитель математики
Кутоманова Е.М.
2015-2016 учебный год
Муниципальное бюджетное общеобразовательное
Слайд 2Линейные неравенства
Неравенство вида ах+в≥0, где а, в - любые числа, а≠0,
называется линейным.
Например: а) 0,5х≤0
б) -3х>0
в) 2,84х-5,68>0
Например: а) 0,5х≤0
б) -3х>0
в) 2,84х-5,68>0
Слайд 3Свойства неравенств:
1.Из любой части неравенства можно переносить в другую любое слагаемое
с противоположным знаком, не меняя при этом знак неравенства.
Например:
3х+6<-х+13
3х+х<-6+13
Например:
3х+6<-х+13
3х+х<-6+13
Слайд 4 2.Обе части неравенства можно умножить или разделить на одно
и то же положительное число не меняя при этом знак неравенства.
Например:
а) 3х>9
3х:3>9:3
х>3
б) 0,5х<0,25
2·0,5х<2·0,25
х<0,5
Например:
а) 3х>9
3х:3>9:3
х>3
б) 0,5х<0,25
2·0,5х<2·0,25
х<0,5
Слайд 5
3.Обе части неравенства можно умножить или разделить на одно
и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Например:
а) -4х≤2
-4х:(-4)≥2:(-4)
х≥-0,5
б) -0,3х<-6
-0,3х:(-0,3)>-6:(-0,3)
х>20
Например:
а) -4х≤2
-4х:(-4)≥2:(-4)
х≥-0,5
б) -0,3х<-6
-0,3х:(-0,3)>-6:(-0,3)
х>20
Слайд 7
Чтобы решить квадратное неравенство методом парабол, надо:
1. рассмотреть функцию у=ах²+вх+с, определить направление ветвей параболы;
2. решить квадратное уравнение ах²+вх+с=0;
3. схематически построить параболу, учитывая направление ветвей и точки пересечения с осью Ох;
4. учитывая знак неравенства, выбрать нужные промежутки и записать ответ.
Слайд 12 1.Решить неравенство:
-х²+7х-12≥0
Рассмотрим функцию у=-х²+7х-12
Коэффициент а=-1,значит ветви параболы направлены вниз.
Решим уравнение -х²+7х-12=0
D=49-48=1
х₁=(-7+1):(-2); х₂=(-7-1):(-2)
х₁=3; х₂= 4
х₁=(-7+1):(-2); х₂=(-7-1):(-2)
х₁=3; х₂= 4
х
3
4
Слайд 132.Решим неравенство
х²-4>0
у=х²-4,
а=1- ветви параболы направлены вверх;
х²-4=0
х²=4
х=±2
Строим
параболу (схематично)
х
-2
2