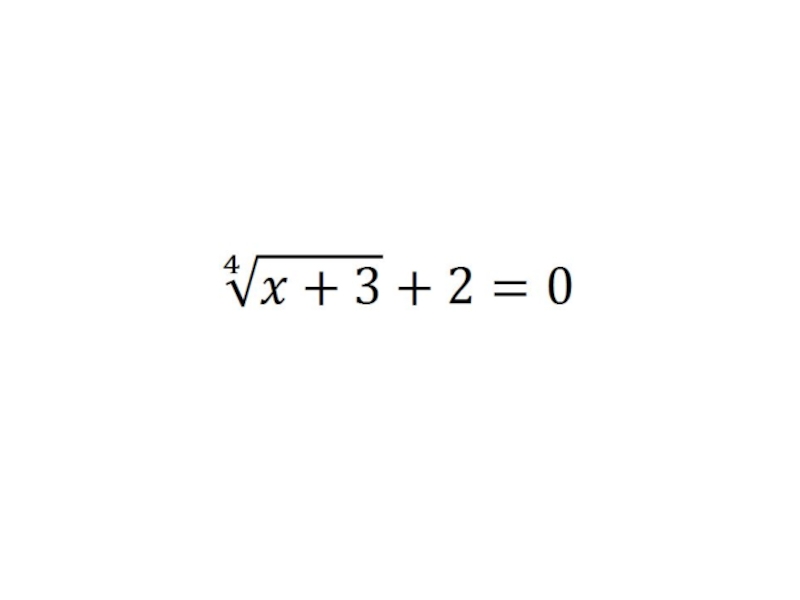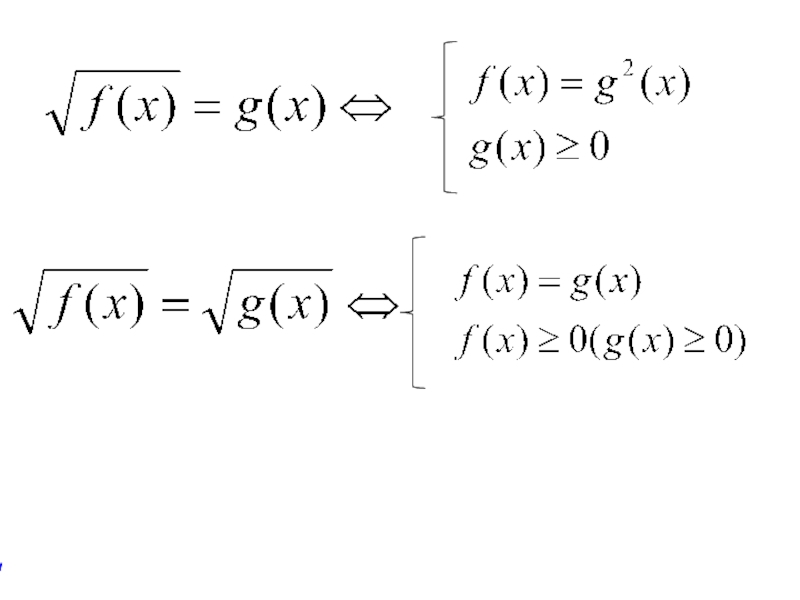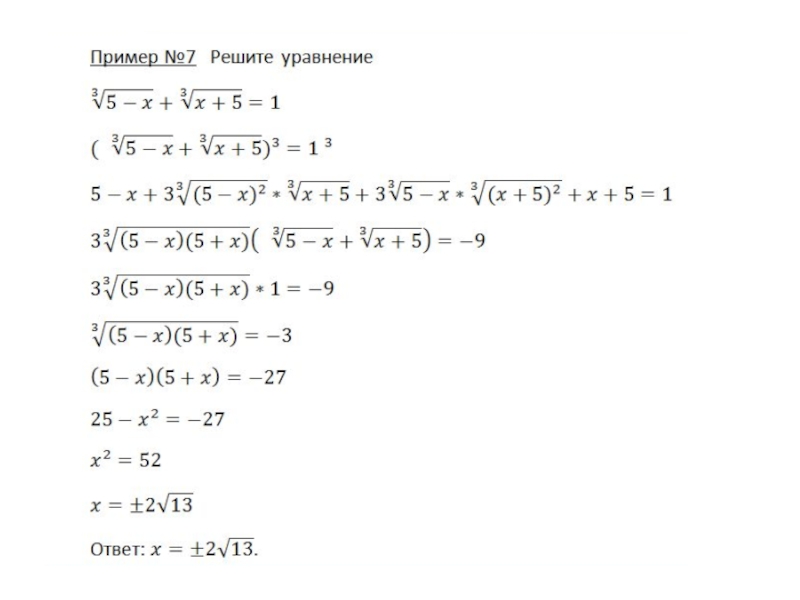- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Решение иррациональных неравенств (10 класс)
Содержание
- 1. Презентация по алгебре на тему Решение иррациональных неравенств (10 класс)
- 2. Иррациональным уравнением называется уравнение, содержащее неизвестную под
- 3. Основные методы решения иррациональных уравнений: возведение в
- 4. Дополнительные методы решения иррациональных уравнений: умножение на
- 5. Слайд 5
- 6. Метод возведения в степень обеих частей уравнения:1)
- 7. Метод возведения в степень обеих частей уравнения:
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Метод введения новой переменной
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Метод разложения на множителиДля решения иррациональных уравнений
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Дополнительные методы решения иррациональных уравнений:метод «пристального взгляда»
- 32. Метод анализа уравненияСвойства корней, которые используют при
- 33. Слайд 33
- 34. Слайд 34
- 35. Метод использования монотонности функции Сформулируем два свойства монотонных
- 36. Метод использования монотонности функций Теорема о корне Пусть
- 37. Слайд 37
- 38. Метод перехода к уравнению с модулем
- 39. Слайд 39
- 40. Слайд 40
Иррациональным уравнением называется уравнение, содержащее неизвестную под знаком радикала, а также под знаком возведения в дробную степень. Например,
Слайд 2Иррациональным уравнением называется уравнение, содержащее неизвестную под знаком радикала, а также
под знаком возведения в дробную степень. Например,
Слайд 3
Основные методы решения иррациональных уравнений:
возведение в степень обеих частей
уравнения;
введение новой переменной;
разложение на множители.
Слайд 4
Дополнительные
методы решения иррациональных уравнений:
умножение на сопряженное;
переход к
уравнению с модулем;
метод «пристального взгляда»
(метод анализа уравнения);
использование монотонности функции.
Слайд 6
Метод возведения в степень
обеих частей уравнения:
1) Если иррациональное уравнение содержит
только один радикал, то нужно записать так, чтобы в одной части знака равенства оказался только этот радикал. Затем обе части уравнения возводят в одну и ту же степень, чтобы получилась рациональное уравнение.
Слайд 7
Метод возведения в степень обеих частей уравнения:
2) Если в иррациональном
уравнении содержится два или более радикала, то сначала изолируется один из радикалов, затем обе части уравнения возводят в одну и ту же степень, и повторяют операцию возведения в степень до тех пор, пока не получится рациональное уравнение.
Слайд 22
Метод введения новой переменной
Данный метод применяется
в том случае, когда в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл принять это выражение за новую переменную и решить уравнение сначала относительно введенной неизвестной, а потом найти исходную величину.
Слайд 27Метод разложения на множители
Для решения иррациональных уравнений данным методом следует пользоваться
правилом:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей, входящих в произведение; равен нулю; а остальные при этом имеют смысл.
Уравнение равносильно совокупности
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей, входящих в произведение; равен нулю; а остальные при этом имеют смысл.
Уравнение равносильно совокупности
1)
2)
Слайд 31
Дополнительные методы решения иррациональных уравнений:
метод «пристального взгляда»
(метод анализа
уравнения);
использование монотонности функции;
переход к уравнению с модулем.
использование монотонности функции;
переход к уравнению с модулем.
Слайд 32
Метод анализа уравнения
Свойства корней, которые используют при решении уравнений данным способом:
1. Все корни четной степени являются арифметическими, то есть если подкоренное выражение отрицательно, то корень лишен смысла; если подкоренное выражение равно нулю, то корень так же равен нулю; если подкоренное выражение положительно, то значение корня положительно.
2. Все корни нечетной степени определены при любом значении подкоренного выражения.
3. Функции и
являются возрастающими в своей области определения.
Слайд 35
Метод использования
монотонности функции
Сформулируем два свойства монотонных функций:
1. Сумма возрастающих
(убывающих) функций – функция возрастающая (соответственно, убывающая) на их общей области определения.
2. Разность возрастающей и убывающей (соответственно, убывающей и возрастающей) функций – функция возрастающая (убывающая) на их общей области определения.
Использование монотонности функций, входящих в уравнение, нередко значительно упрощают техническую часть решения.
Слайд 36
Метод использования монотонности функций
Теорема о корне
Пусть y=f(x) – монотонная на
некотором промежутке функция. Тогда при любом значении а уравнение f(x)=a имеет на этом промежутке не более одного корня.
