- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Решение тригонометрических уравнений(10класс)
Содержание
- 1. Презентация по алгебре на тему Решение тригонометрических уравнений(10класс)
- 2. ДЕВИЗ УРОКА :Ум заключается не только в знании, но и в умении применять знания на практике.Аристотель.
- 3. Оцените свои знания и умения на уроке. Выборы лидеров группы
- 4. ЦЕЛИ: Систематизировать знания и навыки необходимые при
- 5. ФРОНТАЛЬНЫЙ ОПРОС:1.Формулы корней простых тригонометрических уравнений.2.Частные случаи простых тригонометрических уравнеий.3. Ассоциация.(работа с постером)
- 6. Формулы корней простых тригонометрических уравнений1.cost = а
- 7. АссоциацияТРИГОНОМЕТРИЯ
- 8. Сопоставьте следующие колонки таблицы: Работа в группах
- 9. МАТ.ДИКТАНТ (РАБОТА В ПАРАХ)
- 10. ОТВЕТЫ:
- 11. Работа в группах 1. Решить данные уравнения.2.Решения обсудить в группе.3.Решения записать на доске.
- 12. Решение простейших уравнений1) tg2x = -1
- 13. Другие тригонометрические уравнения1.Сводимые к квадратным
- 14. РАЗМИНКА
- 15. Работа по сборнику тестов 2013 года.2013год1) Вариант
- 16. Все понятно , легко, нет вопросовВозникали трудности , есть вопросыТрудно, много вопросов РЕФЛЕКСИЯ
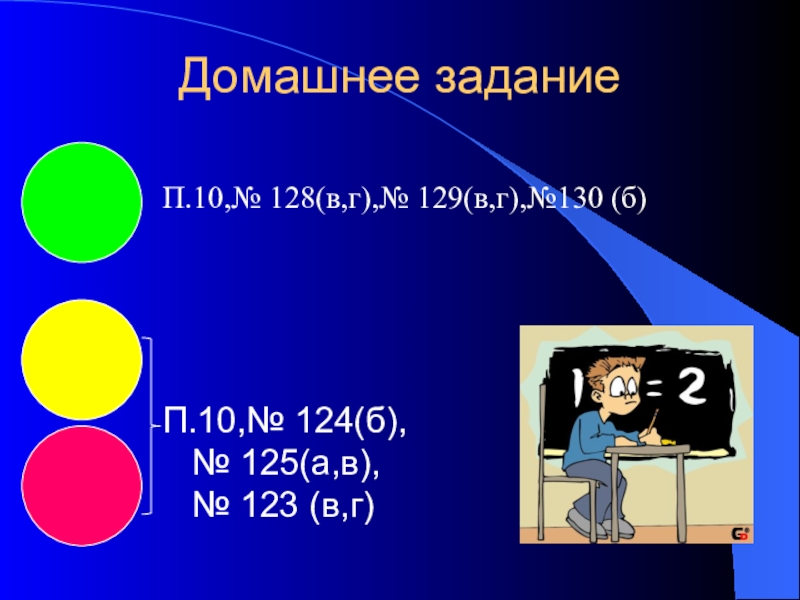
- 17. Домашнее заданиеП.10,№ 128(в,г),№ 129(в,г),№130 (б)П.10,№ 124(б), № 125(а,в), № 123 (в,г)
- 18. Знание – столь
- 19. Спасибо за урок!
Слайд 2ДЕВИЗ УРОКА :
Ум заключается не только в знании, но и в
Аристотель
.
Слайд 4ЦЕЛИ:
Систематизировать знания и навыки необходимые при решении всех видов тригонометрических
Слайд 5ФРОНТАЛЬНЫЙ ОПРОС:
1.Формулы корней простых тригонометрических уравнений.
2.Частные случаи простых тригонометрических уравнеий.
3. Ассоциация.(работа
Слайд 6Формулы корней простых тригонометрических уравнений
1.cost = а , где |а| ≤
Частные случаи
1)cost=0
t = π/2+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ
2.sint = а, где | а |≤ 1
Частные случаи
1)sint=0
t = 0+πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)sint = - 1
t = - π/2+2πk‚ kЄZ
3. tgt = а, аЄR
t = arctg а + πk‚ kЄZ
4. ctgt = а, аЄR
t = arcctg а + πk‚ kЄZ
Слайд 11Работа в группах
1. Решить данные уравнения.
2.Решения обсудить в группе.
3.Решения записать
Слайд 12Решение простейших уравнений
1) tg2x = -1
2x = arctg
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
2) cos(x+π/3) = ½
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.
Слайд 13Другие тригонометрические уравнения
1.Сводимые к квадратным
a∙sin²x +
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и
решить простые уравнения.
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = m
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
Слайд 15Работа по сборнику тестов 2013 года.
2013год
1) Вариант 2 , №6
2) Вариант 4 , № 6 .
3) Вариант 6 , № 6 .
4) Вариант 10 , № 9 .
5) Вариант 17 , № 12 .
6) Вариант 18, № 13 .
Слайд 16
Все понятно , легко,
нет вопросов
Возникали трудности , есть вопросы
Трудно, много вопросов
РЕФЛЕКСИЯ
Слайд 18
Знание –
столь драгоценная вещь, что его не зазорно добывать из