он, он бы нам помог
При счёте, ну и что же это?
Процент
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему: Процентные расчеты
Содержание
- 1. Презентация по алгебре на тему: Процентные расчеты
- 2. Для чего нужны проценты в реальной жизни?Столкнувшись
- 3. Примеры применения процентов в реальной жизни В
- 4. Люди давно заметили, что сотые доли величин
- 5. Проценты широко использовались в Древнем Риме. Римляне
- 6. Интересно происхождение символа %. Как предполагается, он
- 7. Устно Представьте данные десятичные дроби в
- 8. Устно Представьте проценты десятичными дробями: 2%;
- 9. Задача 1 Сколько кг соли в
- 10. Задача 2 Из хлопка-сырца получается 24%
- 11. Задача 3 При плановом задании 60
- 12. Задача 4 Сплав содержит 10 кг
- 13. Виды задач на процентыНахождение: а)процентов от данного числа б)числа по его процентам в) процентного отношения чисел
- 14. Процентные расчетыУрок 1
- 15. Слайд 15
- 16. Слайд 16
- 17. Учебник № 529, 531, 533, 535
Для чего нужны проценты в реальной жизни?Столкнувшись с процентами в первый раз мы вдруг замечаем, что они сопровождают нас повсюду – не только в школе (на уроках математики, физики, химии, биологии, географии и т.д.), но и
Слайд 2Для чего нужны проценты в реальной жизни?
Столкнувшись с процентами в первый
раз мы вдруг замечаем, что они сопровождают нас повсюду – не только в школе (на уроках математики, физики, химии, биологии, географии и т.д.), но и в повседневной жизни: в магазине (особенно во время скидок), на работе (повышение и понижение зарплаты), в банке, на производстве, в СМИ, в интернете, при проведении статистических исследований и многом другом.
Слайд 3Примеры применения процентов в реальной жизни
В выборах приняли участие 63,9%
избирателей.
Количество мальчиков составляло 50% от количества девочек.
Рейтинг победителя в хит-параде равен 67%.
Промышленное производство сократилось на 8,4%.
Уровень инфляции составляет 8% в год.
Банк начисляет 10% годовых.
Молоко содержит 3.1% жира.
Материал содержит 60% хлопка и 40% полиэстера.
Уровень преступности в городе вырос на 1,2%.
Получить 150% выгоды от продажи и т.д.
Количество мальчиков составляло 50% от количества девочек.
Рейтинг победителя в хит-параде равен 67%.
Промышленное производство сократилось на 8,4%.
Уровень инфляции составляет 8% в год.
Банк начисляет 10% годовых.
Молоко содержит 3.1% жира.
Материал содержит 60% хлопка и 40% полиэстера.
Уровень преступности в городе вырос на 1,2%.
Получить 150% выгоды от продажи и т.д.
Слайд 4Люди давно заметили, что сотые доли величин удобны в практической деятельности.
Поэтому для них было придумано специальное название и обозначение
процент
процент
Слайд 5Проценты широко использовались в Древнем Риме. Римляне брали с должника лихву
(т.е. деньги сверх того, что было дано в долг). При этом говорили: «на каждые 100 сестерциев долга заплатишь 16 сестерциев лихвы». Так как слова «на сто» звучали по-латыни «про центум», то сотую часть и стали называть процентом.
Слайд 6Интересно происхождение символа %.
Как предполагается, он стал использоваться благодаря опечатке.
В рукописях словосочетание «pro centum» часто заменяли словом «cento» - «сто» и писали его сокращённо – cto. В 1685 году в Париже была напечатана книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %. После этого многие математики также стали для обозначения процентов употреблять знак %, и постепенно он получил всеобщее признание.
Слайд 9Задача 1
Сколько кг соли в 10 кг соленой воды,
если процентное содержание соли 15%.
1) 15 % = 0,15
2) 10 · 0,15 = 1,5 (кг)
Ответ: 1,5 кг соли.
1) 15 % = 0,15
2) 10 · 0,15 = 1,5 (кг)
Ответ: 1,5 кг соли.
Слайд 10Задача 2
Из хлопка-сырца получается 24% волокна. Сколько надо взять
хлопка-сырца, чтобы получить 480 кг волокна.?
1) 24 % = 0,24
2) 480 : 0,24 = 48000 : 24 = 2000 (кг)
Ответ: Надо взять 2 т хлопка-сырца.
1) 24 % = 0,24
2) 480 : 0,24 = 48000 : 24 = 2000 (кг)
Ответ: Надо взять 2 т хлопка-сырца.
Слайд 11Задача 3
При плановом задании 60 автомобилей в день завод
выпустил 66 автомобилей. На сколько процентов завод перевыполнил план?
1) 66 – 60 = 6 (дет.) – больше плана
2) 6 : 60 = 0,1
3) 0,1 = 10%
Ответ: Завод перевыполнил план на 10%.
1) 66 – 60 = 6 (дет.) – больше плана
2) 6 : 60 = 0,1
3) 0,1 = 10%
Ответ: Завод перевыполнил план на 10%.
Слайд 12Задача 4
Сплав содержит 10 кг олова и 15 кг
цинка. Каково процентное содержание олова и цинка в сплаве?
1) 10 + 15 = 25 (кг) – масса сплава
2) 10 : 25 = 0,4 = 40% -содержание олова
3) 15 : 25 = 0,6 = 60% - содержание цинка
Ответ: В сплаве содержится 40% олова и 60% цинка.
1) 10 + 15 = 25 (кг) – масса сплава
2) 10 : 25 = 0,4 = 40% -содержание олова
3) 15 : 25 = 0,6 = 60% - содержание цинка
Ответ: В сплаве содержится 40% олова и 60% цинка.
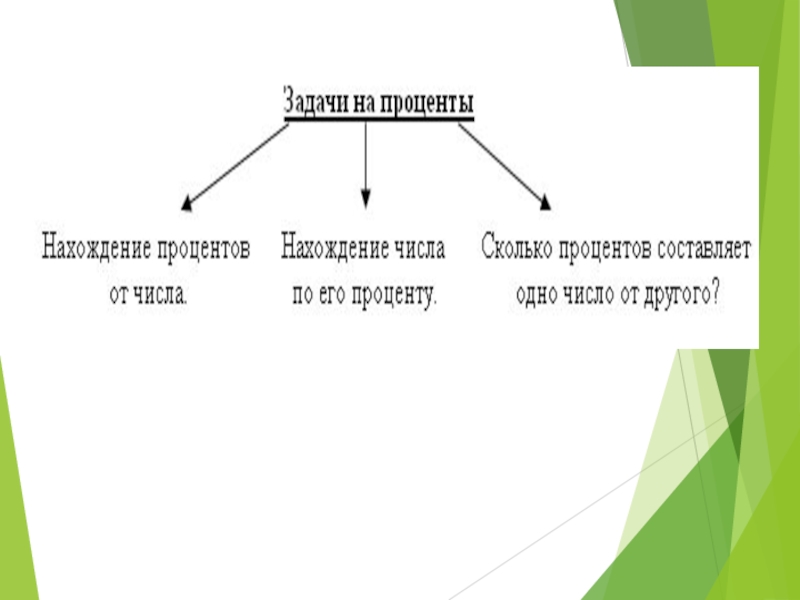
Слайд 13Виды задач на проценты
Нахождение:
а)процентов от данного числа
б)числа
по его процентам
в) процентного отношения чисел
в) процентного отношения чисел
Слайд 17Учебник № 529, 531, 533, 535 Домашнее задание: стр. 293 п. 38-40 повторить №
530, 532, 534, 537
Составить задачи, используя жизненные ситуации, записать на отдельных листах (с решением).