- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Производная
Содержание
- 1. Презентация по алгебре на тему Производная
- 2. Определение производной
- 3. Понятие "производная" возникло в связи с необходимостью
- 4. Геометрический смысл производной Производная функции, вычисленная
- 5. Найти угловой коэффициент касательной, проведенной к графику функции в точке с абсциссойРешениеОтвет: k = 1
- 6. 2) Угловой коэффициент касательной, проведенной к графику
- 7. 3) К графику функции y =
- 8. 4) Функции y = f(x) определена
- 9. Физический (механический) смысл производнойПроизводная от координаты
- 10. ПримерМатериальная точка движется по прямой так, что
- 11. Широкий спектр применения производной Многие задачи математики
Определение производной
Слайд 3Понятие "производная" возникло в связи с необходимостью решения ряда задач физики,
механики и математики.
Честь открытия основных законов математического анализа принадлежит английскому ученому Ньютону и немецкому математику Лейбницу.
Лейбниц рассматривал задачу о проведении касательной к произвольной кривой.
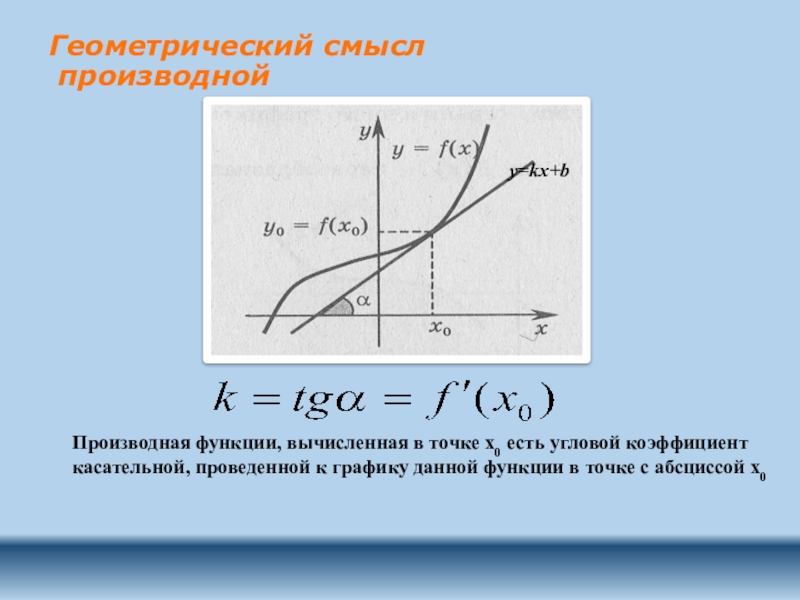
Слайд 4Геометрический смысл
производной
Производная функции, вычисленная в точке х0 есть угловой коэффициент
касательной, проведенной к графику данной функции в точке с абсциссой х0
y=kx+b
Слайд 5Найти угловой коэффициент касательной, проведенной к графику функции
в точке с
абсциссой
Решение
Ответ: k = 1
Слайд 62) Угловой коэффициент касательной, проведенной к графику функции в точке (-2;7),
равен 4. Найдите
Решение
Значит,
Ответ:
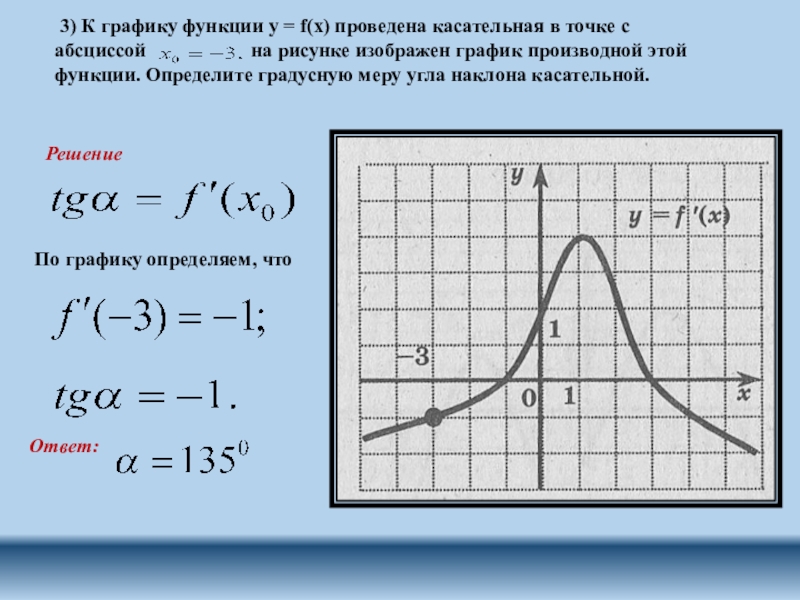
Слайд 7 3) К графику функции y = f(x) проведена касательная в
точке с абсциссой на рисунке изображен график производной этой функции. Определите градусную меру угла наклона касательной.
Решение
По графику определяем, что
Ответ:
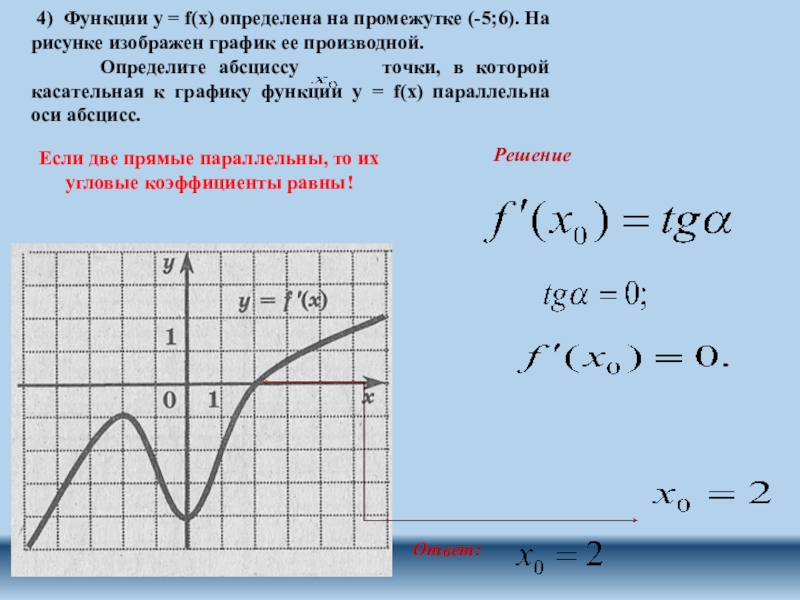
Слайд 8 4) Функции y = f(x) определена на промежутке (-5;6). На
рисунке изображен график ее производной.
Определите абсциссу точки, в которой касательная к графику функции y = f(x) параллельна оси абсцисс.
Определите абсциссу точки, в которой касательная к графику функции y = f(x) параллельна оси абсцисс.
Решение
Если две прямые параллельны, то их угловые коэффициенты равны!
Ответ:
Слайд 9Физический (механический)
смысл производной
Производная от координаты (от закона движения) есть скорость
Производная,
вычисленная в определенной точке есть мгновенная скорость
Слайд 10Пример
Материальная точка движется по прямой так, что ее скорость в момент
времени t равна
Найдите ускорение точки в момент времени t = 3.
Решение
Найдите ускорение точки в момент времени t = 3.
Решение
Ответ:
Слайд 11Широкий спектр применения производной Многие задачи математики ,физики, реального мира решаются с
помощью производной. При помощью производной можно найти скорость , ускорение, мощность, силу тока и многие другие величины. Операции нахождения производной функции называется дифференцированием.
