- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Примеры комбинаторных задач (9 класс)
Содержание
- 1. Презентация по алгебре на тему Примеры комбинаторных задач (9 класс)
- 2. Цель:Рассмотреть некоторые задачи комбинаторики.
- 3. Задача 1. На завтрак Вова может
- 4. Такие задачи получили название комбинаторных задач, а
- 5. Термин «комбинаторика» был введён в математический обиход
- 6. решение методом перебора; решение с помощью
- 7. У Ирины 5 подруг: Вера, Зоя, Марина,
- 8. 1) Составим все пары, в которые входит
- 9. Решение: Для того, чтобы не пропустить и
- 10. На примерах учимсяСколько трехзначных чисел можно составить
- 11. Заметим, что ответ на вопрос,
- 12. «Если объект А можно выбрать m способами,
- 13. На примерах учимсяВ класс пришли четыре новых
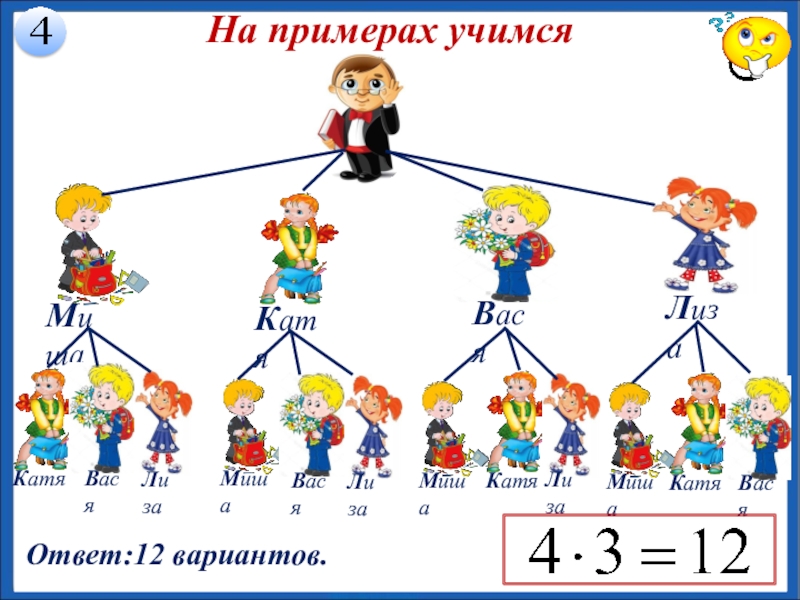
- 14. На примерах учимсяОтвет:12 вариантов.
- 15. Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?12459024101412202224404244505254909294На примерах учимсяОтвет:15 чисел.
- 16. Пятеро друзей встретились после каникул и обменялись
- 17. На примерах учимсяПятеро друзей встретились после каникул
- 18. На примерах учимсяРешите задачу, используя графШесть семей
- 19. А теперь, девчата, встали. Быстро руки вверх
- 20. На примерах учимся№718(б),№719
- 21. Что изучает комбинаторика?Кем был введен в математический
- 22. Учиться –все равно, что грести против течения
- 23. Сегодня на уроке я запомнила……………..Я научилась……………………………………Я поняла……………………………………......У
Слайд 3 Задача 1.
На завтрак Вова может выбрать плюшку, бутерброд, пряник
Открываем новое
В науке и на практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций.
Слайд 4Такие задачи получили название комбинаторных задач,
а раздел математики, в котором
Открываем новое
Определение
Слайд 5Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем,
Термин «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Открываем новое
Слайд 6
решение методом перебора;
решение с помощью дерева возможных вариантов;
решение
решение с помощью таблиц;
решение с помощью графов.
Способы решения
комбинаторных задач
Слайд 7У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она
Замечание. При решении для краткости будем писать первые буквы имен.
На примерах учимся
Слайд 81) Составим все пары, в которые входит Вера:
ВЗ, ВМ, ВП, ВС
2)
3) Составим пары, в которые входит Марина, но не входят Вера и Зоя.
Получим 1 пару
ЗМ, ЗП, ЗС
МП, МС
ПС
Всего существует 4+3+2+1=10
Решение
Ответ:10 вариантов.
Вера,
Зоя,
Марина,
Полина,
Света.
Получим 4 пары.
Получим 3 пары.
Получим 2 пары.
4) Составим пары, в которые входит Полина.
На примерах учимся
Слайд 9Решение: Для того, чтобы не пропустить и не повторить ни одного
Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
На примерах учимся
Перебор возможных вариантов
11,
14,
17;
41,
44,
47;
71,
74,
77;
I цифра 1:
I цифра 4:
I цифра 7:
Всего существует 3+3+3=9
Ответ: 9 чисел.
Слайд 10На примерах учимся
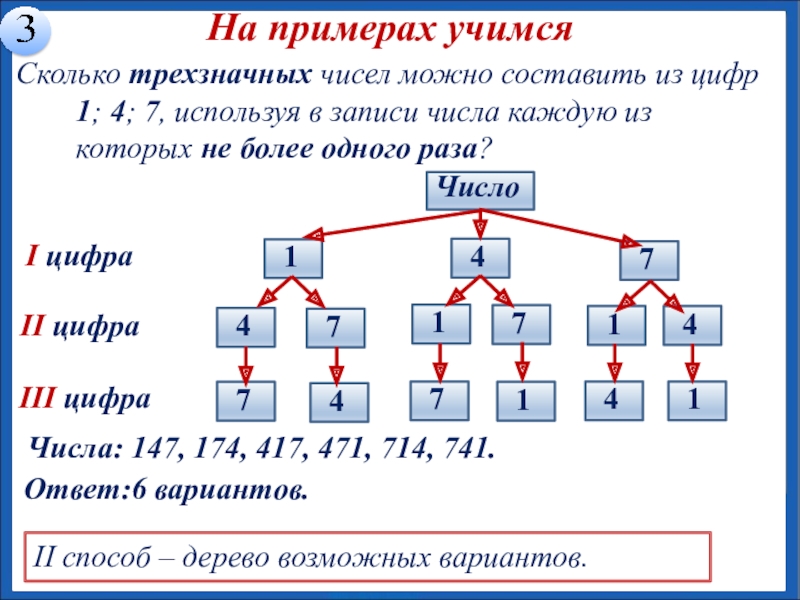
Сколько трехзначных чисел можно составить из цифр 1; 4;
I цифра
II цифра
III цифра
Ответ:6 вариантов.
Числа: 147, 174, 417, 471, 714, 741.
Слайд 11
Заметим, что ответ на вопрос, можно получить, не выписывая
Первую цифру можно выбрать тремя способами.
После выбора первой цифры останутся две.
Вторую цифру можно выбрать двумя способами.
Остается приписать одну цифру.
Следовательно, общее число искомых трехзначных чисел равно произведению
На примерах учимся
Сколько трехзначных чисел можно составить из цифр 1; 4; 7, используя в записи числа каждую из которых не более одного раза?
Слайд 12«Если объект А можно выбрать m способами, а другой объект В
Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения
Открываем новое
Пусть имеем n элементов и надо выбрать из них один за другим k элементов. Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать n2 способами из оставшихся, затем третий элемент можно выбрать n3 способами из оставшихся и т.д., то число способов, которыми могут быть выбраны все k элементов, равно произведению
Слайд 13На примерах учимся
В класс пришли четыре новых ученика Миша, Катя, Вася,
Слайд 15Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
1
2
4
5
9
0
2
4
10
14
12
20
22
24
40
42
44
50
52
54
90
92
94
На примерах учимся
Ответ:15
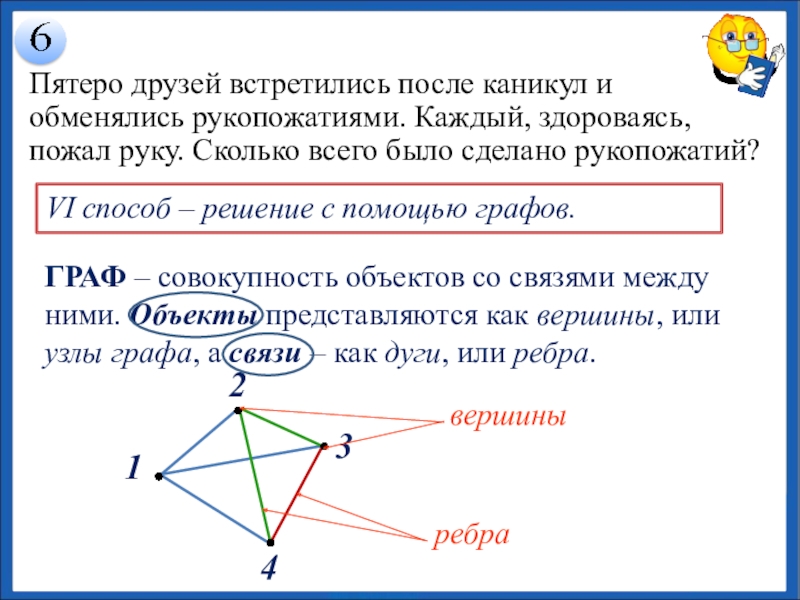
Слайд 16Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал
ГРАФ – совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи – как дуги, или ребра.
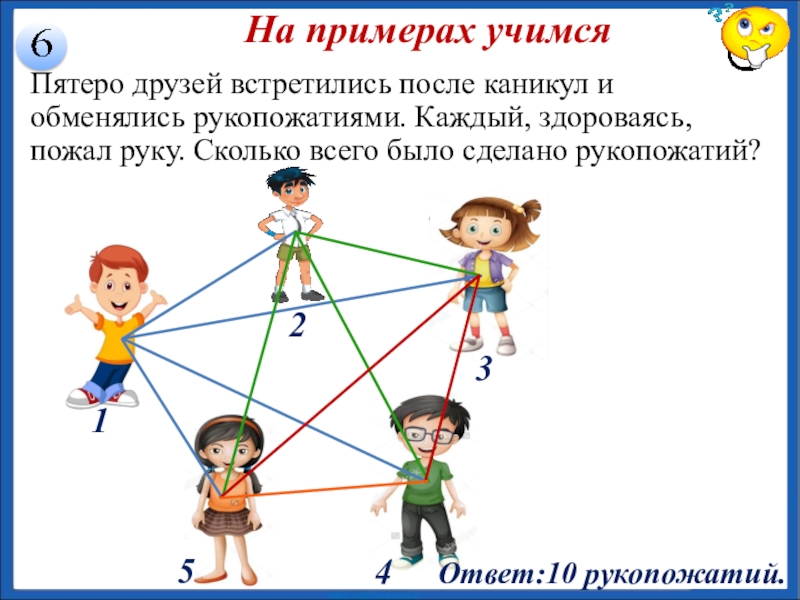
Слайд 17На примерах учимся
Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый,
Ответ:10 рукопожатий.
Слайд 18На примерах учимся
Решите задачу, используя граф
Шесть семей уехали отдыхать в разные
Ответ:15 звонков.
Слайд 19А теперь, девчата, встали.
Быстро руки вверх подняли,
В стороны, вперед, назад.
Физкультминутка.
Повернулись вправо, влево,
Тихо сели, вновь за дело.
Один, два, три, четыре, пять,
Все умеем мы считать.
Отдыхать умеем тоже:
Руки за спину положим,
Голову поднимем выше
И легко – легко подышим.
Слайд 21Что изучает комбинаторика?
Кем был введен в математический обиход термин «комбинаторика»?
Какие способы
Ответим на вопросы
Слайд 22Учиться –все равно, что грести против течения ׃ только перестанешь и
Задания для самоподготовки
Выучить: п.30. Разобрать примеры 1, 2, 3.
Выполнить: № 714, №718(а), №720, №721, №723, №729(а).
Слайд 23Сегодня на уроке я запомнила……………..
Я научилась……………………………………
Я поняла……………………………………......
У меня не получилось………………………
Мне бы
Я справлюсь с домашней работой………...
Закончи предложение: