- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему : Применение производной на исследование монотонности и экстремумов функции ( 10 класс)
Содержание
- 1. Презентация по алгебре на тему : Применение производной на исследование монотонности и экстремумов функции ( 10 класс)
- 2. Математический диктант.1) Функция f(x) возрастает на множестве
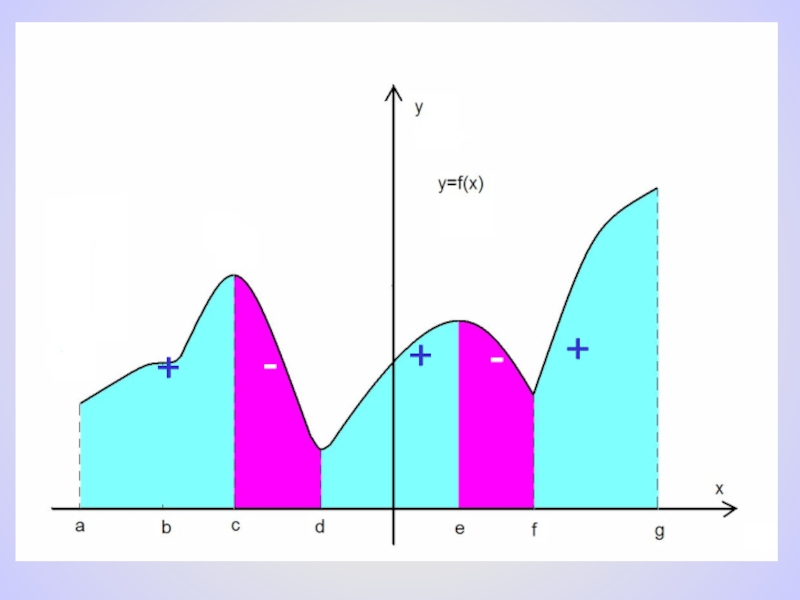
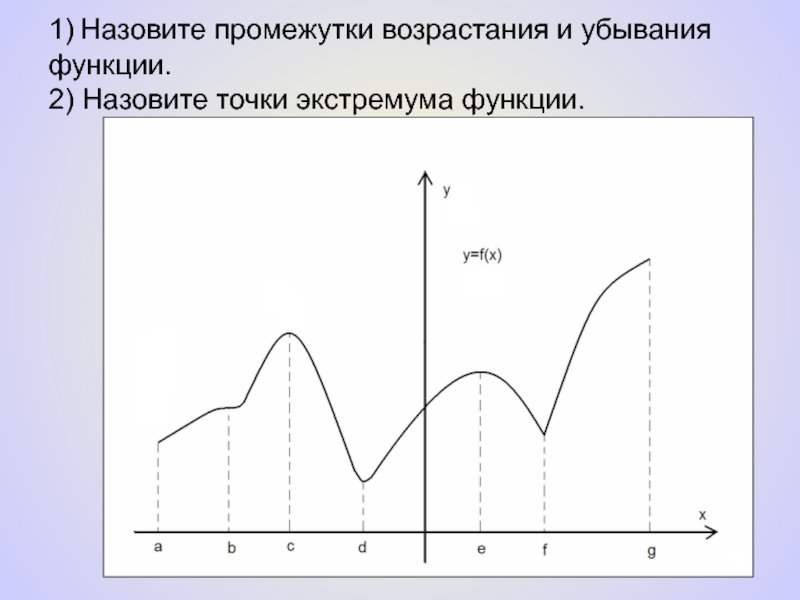
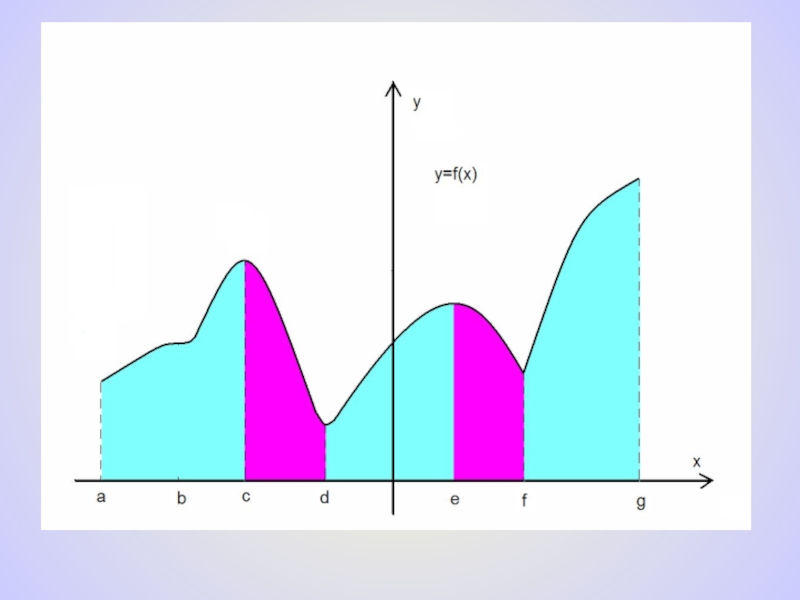
- 3. 1) Назовите промежутки возрастания и убывания функции. 2) Назовите точки экстремума функции.y=f(x)
- 4. Слайд 4
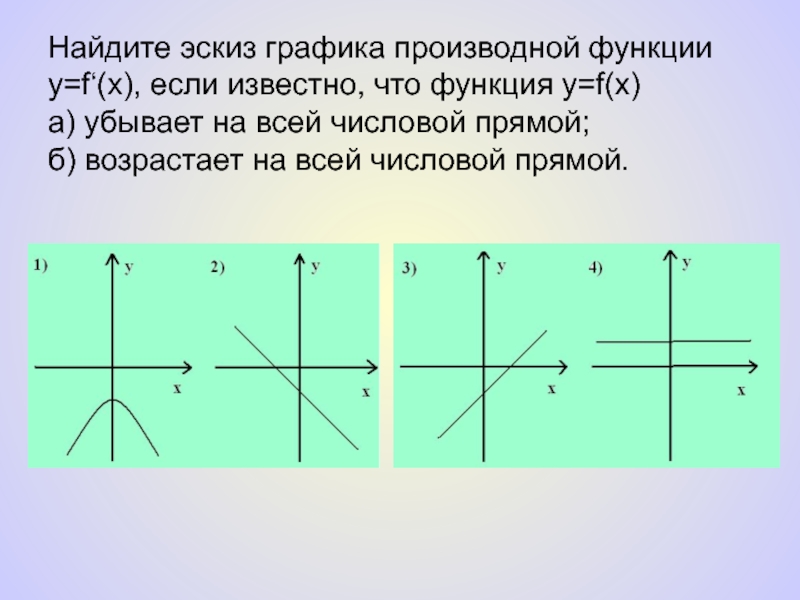
- 5. Найдите эскиз графика производной функции y=f‘(x), если
- 6. Функция определена на [-7;8]. На рисунке изображен
- 7. +++--
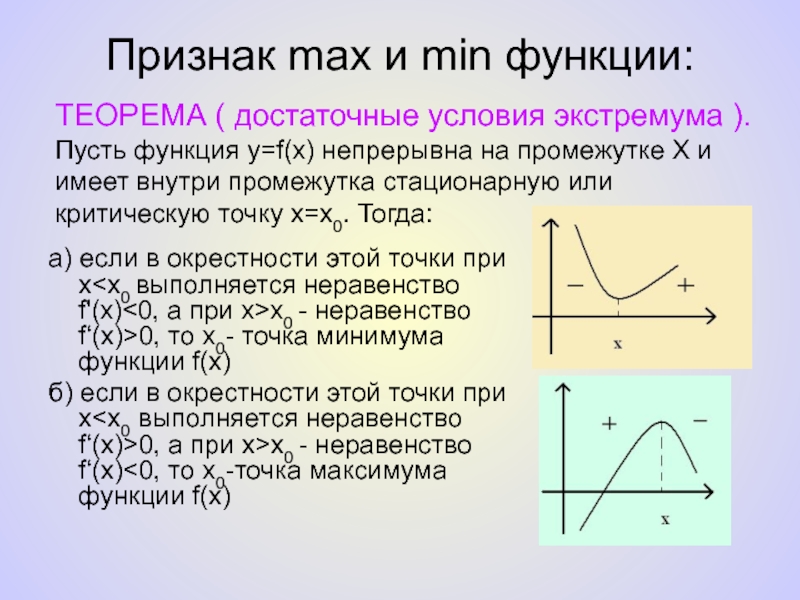
- 8. Признак max и min функции:а) если в окрестности этой точки при x
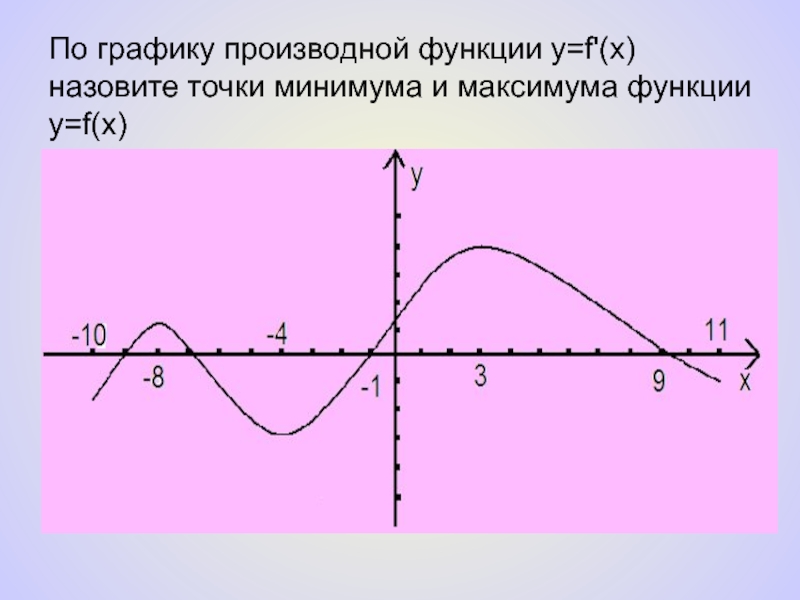
- 9. По графику производной функции y=f'(x) назовите точки минимума и максимума функции y=f(x)
- 10. Найдите промежутки возрастания и убывания функции, точки
- 11. Алгоритм исследования непрерывной функции y=f(x) на монотонность
- 12. Найдите промежутки возрастания и убывания и точки
- 13. Домашнее заданиеЗаписать алгоритм исследования непрерывной функции на
Слайд 2Математический диктант.
1) Функция f(x) возрастает на множестве X, если для любых
2) Если большему значению аргумента соответствует большее значение функции, то функция называется…..
3) Функция f(x) убывает на множестве X,если для любых x1,x2є X: ….. => f (x2) 4) Если ….. значению аргумента соответствует ….. значение функции, то f называется убывающей. 5) Точка x0 называется точкой ….. функции f, если для всех x из ….. x0 выполняется неравенство f(x)≥f(x0) 6) Точка x0 называется точкой максимума функции, если для всех x из окрестности x0 выполняется неравенство ….. f(x2)>f(x1) возрастающей x2>x1 большему меньшее минимума окрестности f(x)≤ f(x0)
Слайд 31) Назовите промежутки возрастания и убывания функции.
2) Назовите точки экстремума функции.
y=f(x)
Слайд 5Найдите эскиз графика производной функции y=f‘(x), если известно, что функция y=f(x)
Слайд 6Функция определена на [-7;8]. На рисунке изображен график её производной. Найдите
![Функция определена на [-7;8]. На рисунке изображен график её производной. Найдите наибольшую из длин промежутков возрастания функции](/img/thumbs/1e61e9c952dcf09e7f69a5a54fdaab96-800x.jpg "Презентация по алгебре на тему : Применение производной на исследование монотонности и экстремумов функции ( 10 класс) Функция определена на [-7;8]. На рисунке изображен график её производной. Найдите")
Слайд 8Признак max и min функции:
а) если в окрестности этой точки при
б) если в окрестности этой точки при x
ТЕОРЕМА ( достаточные условия экстремума ).
Пусть функция y=f(x) непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку x=x0. Тогда:
Слайд 10Найдите промежутки возрастания и убывания функции, точки экстремума и экстремумы
D(f)=R
f(x)=x2-5x+6
f‘(x)=0
x1=2 x2=3
f(x) возрастает на (-∞;2], [3;+∞)
f(x) убывает на [2;3]
Хmax=2 Xmin=3
Ymax=32/3 Ymin=3,5
2
max
3
min
Слайд 11Алгоритм исследования непрерывной функции y=f(x) на монотонность и экстремумы
Найти область
Найти производную функции f‘(x).
Найти стационарные и критические точки.
Решить неравенства f‘(x)>0 и f‘(x)<0 методом интервалов.
Сделать вывод о монотонности функции и о её точках экстремума.
Слайд 12Найдите промежутки возрастания и убывания и точки экстремума функции f(x)=-5x5+3x3.
D(f)=R
f‘(x)=-25x4+9x2=x2(-25x2+9)
f‘(x)=0
x=0 x=±3/5
f(x) возрастает на [-3/5;3/5]
f(x) убывает на (-∞;-3/5], [3/5;+∞)
Xmax=3/5 Xmin=-3/5
Слайд 13Домашнее задание
Записать алгоритм исследования непрерывной функции на монотонность и экстремумы
№ 884(в,г),
№ 887(б), № 888(б)
