- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Применение производной (10 класс)
Содержание
- 1. Презентация по алгебре на тему Применение производной (10 класс)
- 2. Организационный момент.Разминка. Блиц-турнир.« Кто быстрее решит ?»-самостоятельная
- 3. Блиц-турнир1 вариантБлиц-турнир:
- 4. 1) Как обозначается приращение аргумента?
- 5. Δ?
- 6. 2) Чему равна производная скорости?
- 7. а (t)
- 8. 3) Как вычислить производную сложной функции?
- 9. Производную основной функции умножить на производную вспомогательной.
- 10. 4) Какая точка называется точкой максимума?
- 11. Точка, в которой производная меняет знак с + на -.
- 12. 5) Каково поведение функции, если f′(x) > 0?
- 13. Возрастает.
- 14. 6) (sin 2x)′ = ?
- 15. 2 cos2x
- 16. 7) (4х²)′ =
- 17. 8х
- 18. 8) Какие точки называются критическими?
- 19. Точки, в которых производная равна 0 или не существует.
- 20. 2 вариант
- 21. 1) Как обозначается приращение функции?
- 22. ∆ f(x)
- 23. 2) Чему равна производная пути?
- 24. υ (t)
- 25. 3) Как вычислить производную произведения?
- 26. Производная первого множителя умножить на второй плюс первый множитель умножить на производную второго множителя.
- 27. 4) Какое условие выполняется, если f(-x) = f(x)?
- 28. Функция является четной?
- 29. 5) Какая точка называется точкой минимума?
- 30. Точка, в которой производная меняет свой знак с – на +.
- 31. 6) Каково поведение функции, если f′ (x) < 0 ?
- 32. Убывает.
- 33. 7) (5х³)′ = ?
- 34. 15х²
- 35. 8) (cos7x)′ = ?
- 36. - 7 sin7x
- 37. Задание: найти производную.Кто быстрее и правильно решит?
- 38. I вариант(А)
- 39. I вариант(А)
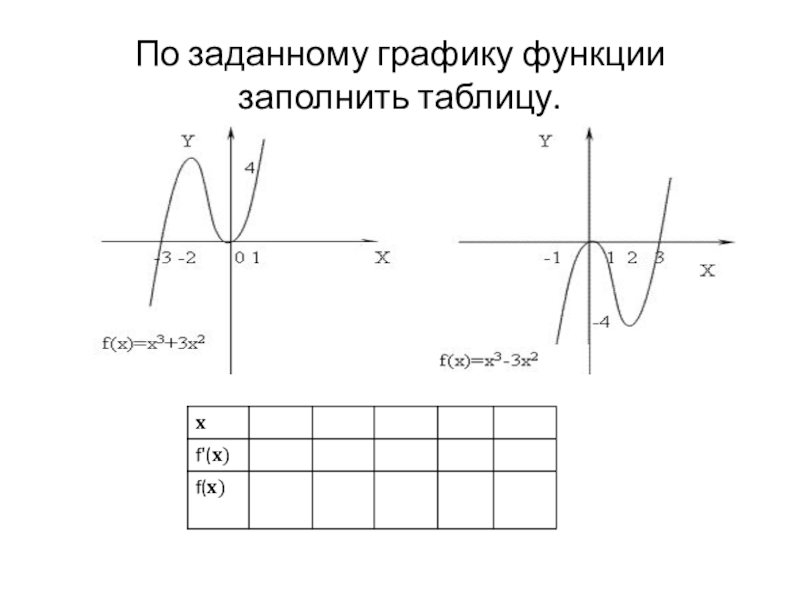
- 40. По заданному графику функции заполнить таблицу.
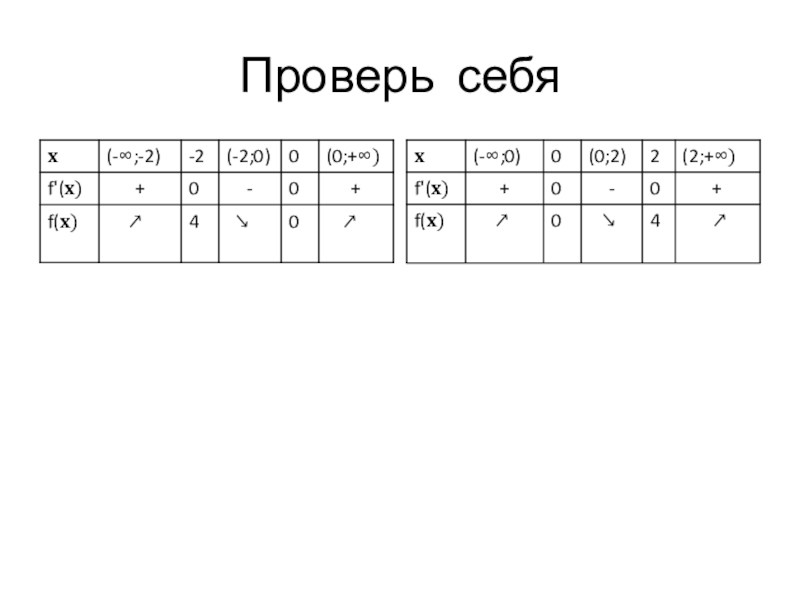
- 41. Проверь себя
- 42. Найди ошибку
- 43. Ньютон
- 44. Лейбниц(XVIIв)
- 45. Тарталья (1500-1557гг.)
- 46. Галилей
- 47. Декарт(XVII)
- 48. Роберваль(XVIIв)
- 49. Л.Грегори(XVIIв)
- 50. Лопиталь (XVIIв)
- 51. Бернулли(XVIII)
- 52. Лагранж(XVIII)
- 53. Эйлер(XVIIв.)
- 54. Гаусс(XVIIв)
- 55. :υ(t) = х/(t) – скоростьa (t)=υ/ (t)
- 56. Задача 1:Какова величина мощности электроплитки, работа которой
- 57. Какую величину имеет
- 58. П (t) = υ / (t) -
- 59. Выбрать оптимальный
- 60. № 538 (2)№ 538 (3)
- 61. I вариант: maxf(?)=f(2,5)=II вариант: max f(?)= f(4)=15
- 62. Страница 151,10 вопросСтраница 151,11 вопросРабота по учебнику «Мектеп»,работа с тестом
- 63. «D» «В»Проверь себя
- 64. Производная какой функции равна?f′ (x): 0; 1;
- 65. Решить тест :учебник «Мектеп» страница 150.Домашнее задание:
Слайд 2Организационный момент.
Разминка. Блиц-турнир.
« Кто быстрее решит ?»-самостоятельная работа.
« Найди ошибку»-коррекционная работа.
Доклады
Решение задач.
Работа по учебнику «Атамура»-решение задач.
Работа по учебнику «Мектеп»-решение тестовых заданий.
Устный счёт-опережающее задание.
Итоги урока.
Домашнее задание.
План урока:
Слайд 26 Производная первого множителя умножить на второй плюс первый
Слайд 38 I вариант(А) II вариант(В)
1)
2) (3sin4x)′ =
3) (-t³/6 + 8t² - 5)′ =
4) (-5cos3x)′ =
III вариант (С)
1)f(?)= , ?₀=-3?
2)f(?)= -
, ?₀=-3
1 ( (2x + 3)³)′ =
2) (4sin5x)′ =
3)f(?)=?²???(½?-¼?),
?₀=½?
Слайд 39 I вариант(А) II вариант(В)
1) 6?-4
2) 12???4?
3)-½?²+16?
4)15???3?
7)6(2?+3)²
III вариант (С)
0
2)-7,75
1) 6(2?+3)²
2) 20???5?
3)?
Слайд 55:
υ(t) = х/(t) – скорость
a (t)=υ/ (t) - ускорение
J (t) =
C(t) = Q/(t) - теплоемкость
d(l)=m/(l) - линейная плотность
K (t) = l/(t) - коэффициент линейного расширения
ω (t)= φ/(t) - угловая скорость
а (t)= ω/(t) - угловое
N(t) = A/(t) – мощность
Физические производные величины
Слайд 56Задача 1:
Какова величина мощности электроплитки, работа которой совершается по закону:
А(t) =
Задача 1:
Слайд 57 Какую величину имеет εi (эдс индукции), возникающая
Ф(t) = 30 cos2 πt (Вб)
Задача 2:
Слайд 58П (t) = υ / (t) - производительность труда,
где υ (t)
J(x) = y / (x) - предельные издержки производства,
где y– издержки производства в зависимости от объема выпускаемой продукции x.
Производная в экономических формулах:
Слайд 59 Выбрать оптимальный объем производства фирмой, функция
π(q) = = q² - 8q + 10
Задача 3:
Слайд 60№ 538 (2)
№ 538 (3)
Найти наибольшее и
Работа по учебнику «Атамура»:
Найти наибольшее и наименьшее значения функции на данном промежутке:[0; 2,5]
Слайд 64Производная какой функции равна?
f′ (x): 0; 1; 3x²; -5; 2x; cos
f(x): x; 2x; 1; x³; 2x³; 4x²; x⁷ ; cosx; x²; -5x; 2 sin2x; sinx.
Выбери правильный ответ! (опережающее задание)






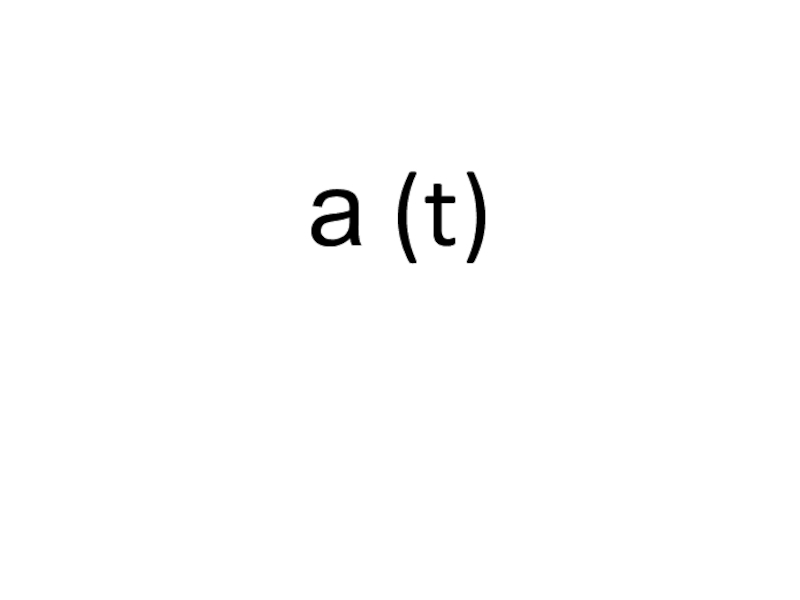






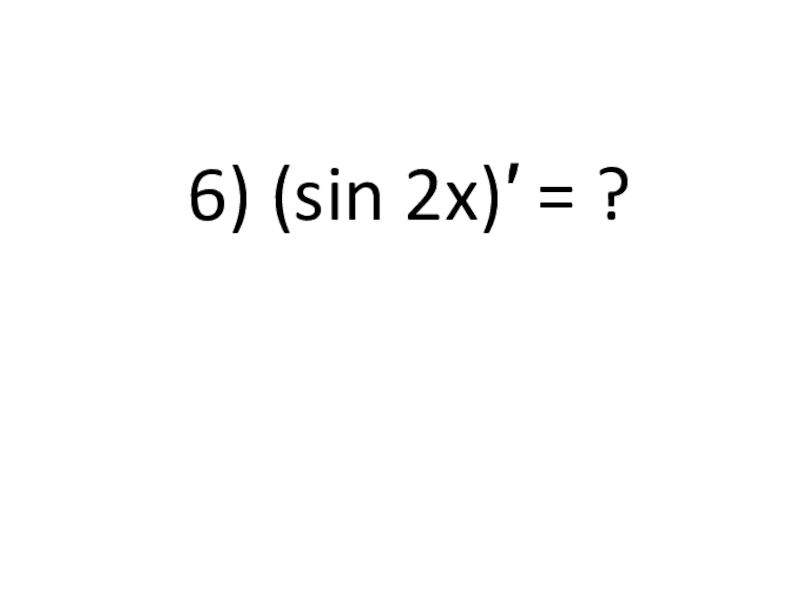
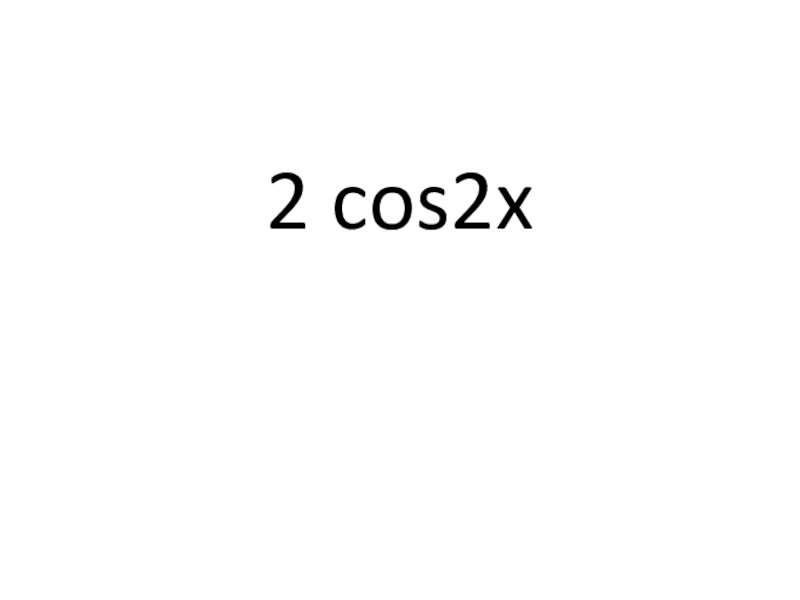
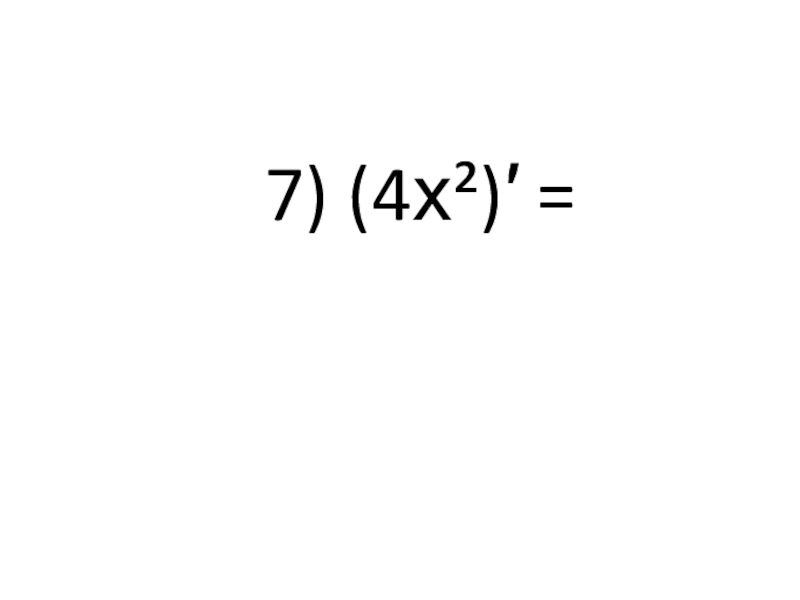
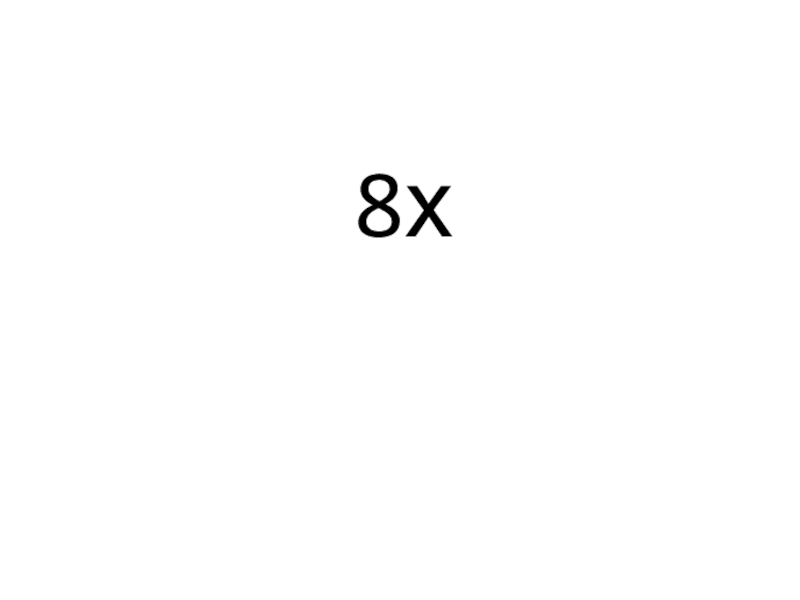




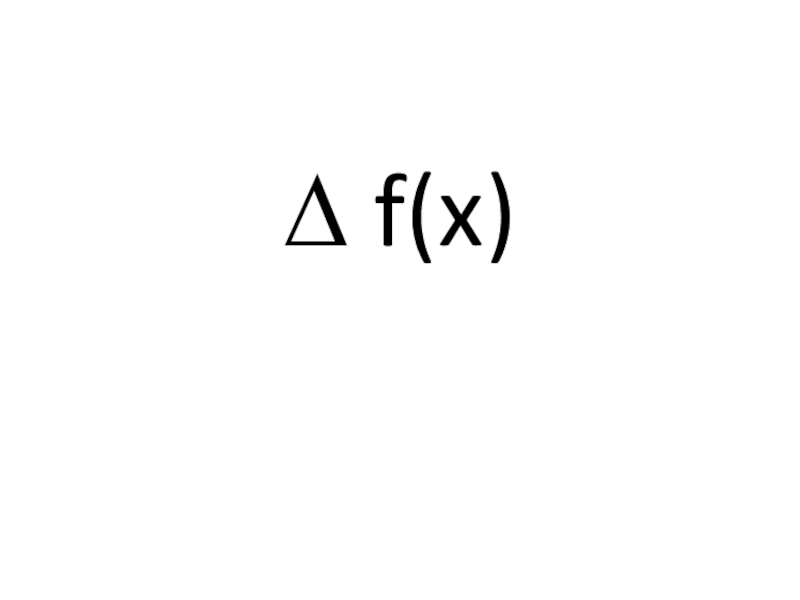

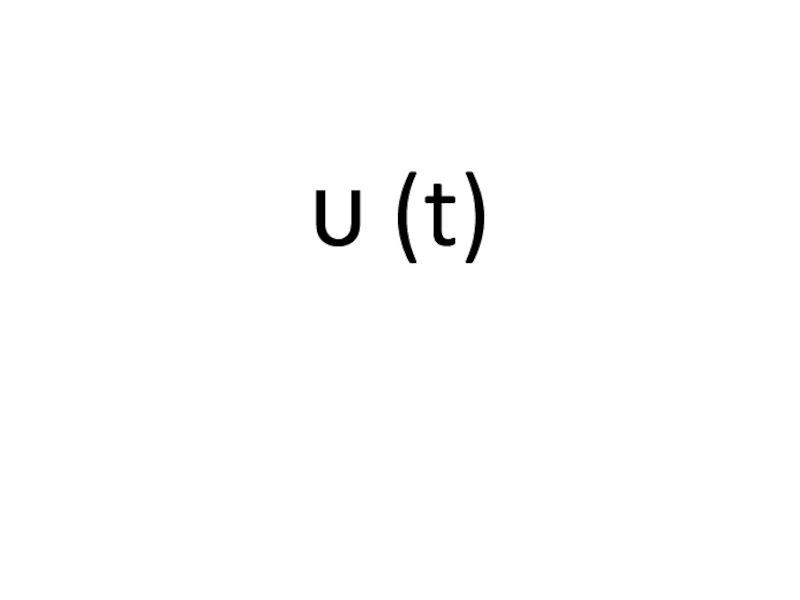








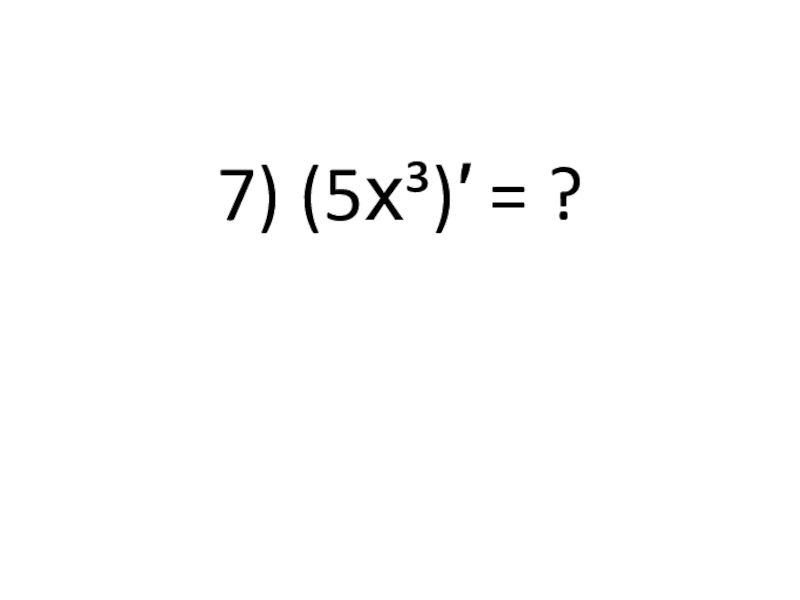
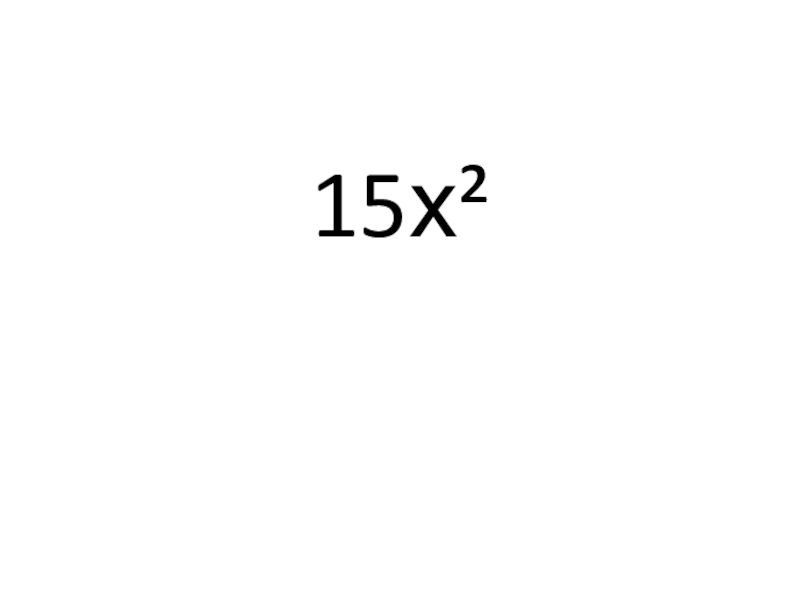
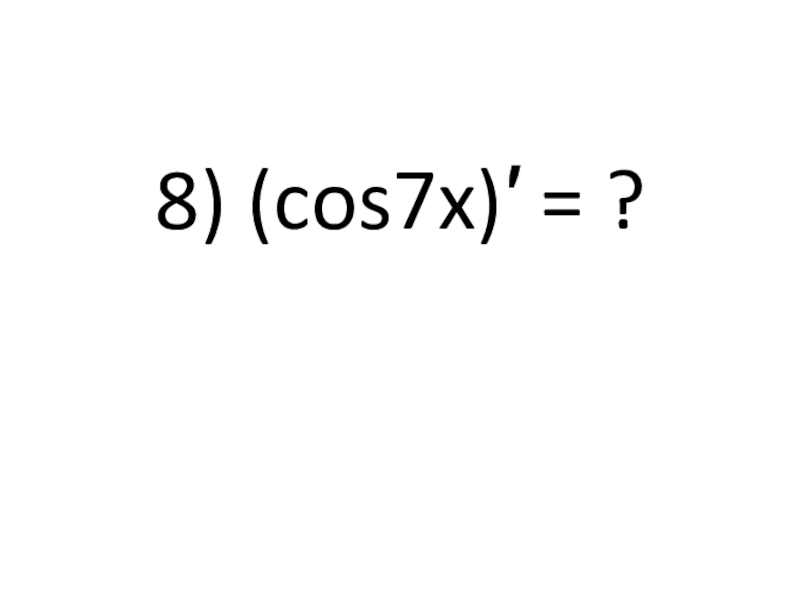
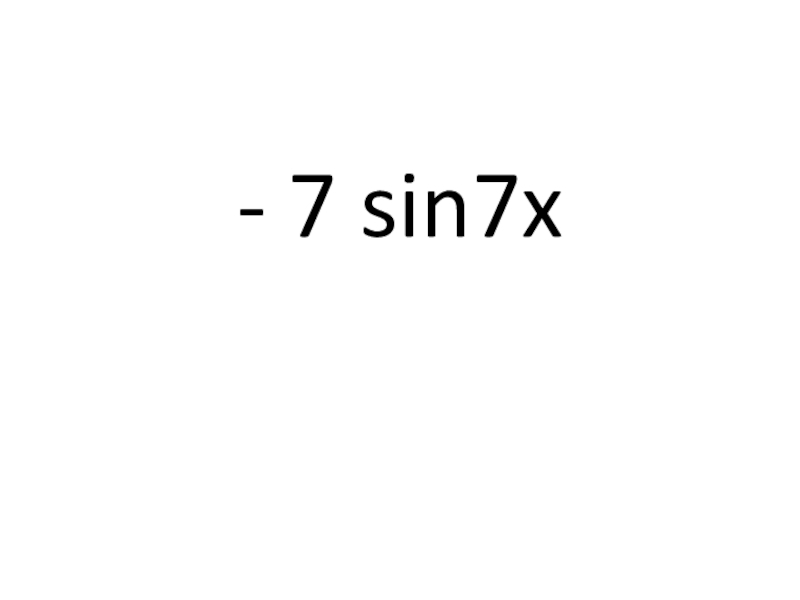





















![Презентация по алгебре на тему Применение производной (10 класс) № 538 (2)№ 538 (3) Найти наибольшее и наименьшее значения № 538 (2)№ 538 (3) Найти наибольшее и наименьшее значения функции на данном промежутке:[0;4]Работа](/img/thumbs/918aca08a9a94c168d8f4f62a21969ea-800x.jpg)










