трапеции. Формула Ньютона-Лейбница."
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Площадь криволинейной трапеции. Формула Ньютона-Лейбница 11 класс
Содержание
- 1. Презентация по алгебре на тему Площадь криволинейной трапеции. Формула Ньютона-Лейбница 11 класс
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Работа в группах1 группа: Найдите площадь фигуры,
- 6. Тест Вычислить площадь фигуры, ограниченной линиями
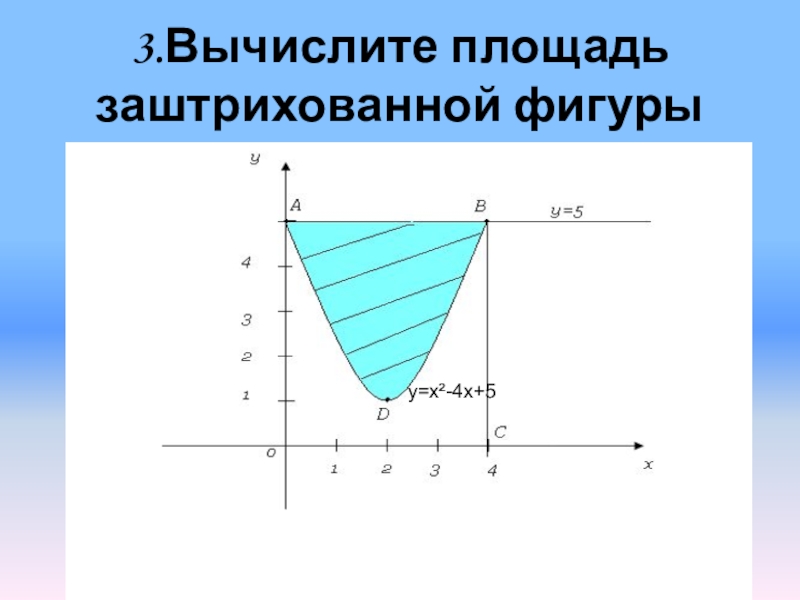
- 7. 3.Вычислите площадь заштрихованной фигурыy=x²-4x+5
- 8. Слайд 8
- 9. 1. Скорость прямолинейного движения точки изменяется по
- 10. Слайд 10
- 11. Слайд 11
Слайд 1Беспалова Людмила Ивановна
ГКОУ «Кочелаевская школа-интернат»
Учитель математики
Тема урока :
" Площадь криволенейной
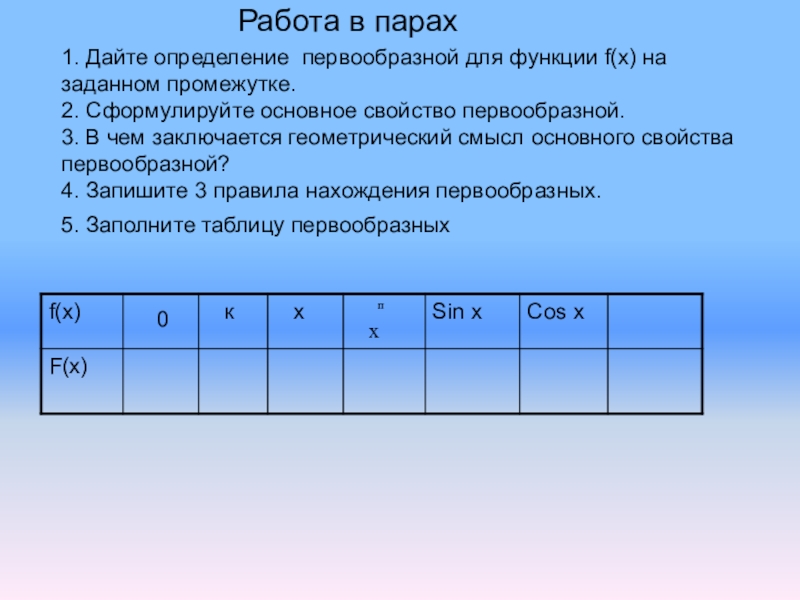
Слайд 3 Работа в парах 1. Дайте
определение первообразной для функции f(х) на заданном промежутке.
2. Сформулируйте основное свойство первообразной.
3. В чем заключается геометрический смысл основного свойства первообразной?
4. Запишите 3 правила нахождения первообразных.
5. Заполните таблицу первообразных
Слайд 5Работа в группах
1 группа: Найдите площадь фигуры, ограниченной линиями
y(x)=x2+2, g(x)=4-x
2 группа:
Найдите площадь фигуры, ограниченной линиями
y(x)=-x2-4x, g(x)=x+4
3 группа: Найдите площадь фигуры, ограниченной линиями
y(x)=4/x2, g(x)=-3x+7
y(x)=-x2-4x, g(x)=x+4
3 группа: Найдите площадь фигуры, ограниченной линиями
y(x)=4/x2, g(x)=-3x+7
Слайд 6Тест
Вычислить площадь фигуры, ограниченной линиями у=х; у=0; х=3.
А)4,5
Б)1,5 В)3 Г)6
2. Вычислить площадь фигуры, ограниченной линиями у=0; y=cosx, Х=; х=
А)1 Б) В) Г)2
3. Вычислить площадь фигуры, ограниченной линиями у=; у=0; х=6.
А)3 Б) В)6 Г)36
4. Вычислить площадь фигуры, ограниченной линиями у= ; х=0; у=0.
А)2 Б); В) 2; Г)3
5. Вычислить площадь фигуры, ограниченной линиями у=3-3;у=0.
А)2 Б)4; В)3; г)6
6. Вычислить площадь фигуры, ограниченной линиями у=; у=0; х=9.
Ответ:
7. Вычислить площадь фигуры, ограниченной параболой у=-3+ 18х -15 и осью абсцисс.
Ответ:
8. Вычислить площадь фигуры, ограниченной линиями у= ++;
у=0; х=0; х= .
2. Вычислить площадь фигуры, ограниченной линиями у=0; y=cosx, Х=; х=
А)1 Б) В) Г)2
3. Вычислить площадь фигуры, ограниченной линиями у=; у=0; х=6.
А)3 Б) В)6 Г)36
4. Вычислить площадь фигуры, ограниченной линиями у= ; х=0; у=0.
А)2 Б); В) 2; Г)3
5. Вычислить площадь фигуры, ограниченной линиями у=3-3;у=0.
А)2 Б)4; В)3; г)6
6. Вычислить площадь фигуры, ограниченной линиями у=; у=0; х=9.
Ответ:
7. Вычислить площадь фигуры, ограниченной параболой у=-3+ 18х -15 и осью абсцисс.
Ответ:
8. Вычислить площадь фигуры, ограниченной линиями у= ++;
у=0; х=0; х= .
Слайд 8 Решение: SABD = SOABC - SOADBC 1.SOABC = 5 x 4 = 20(кв.
ед.)
2.SOADBC = ∫ (x2 – 4x + 5)dx =
(x3 : 3) – 2x2 + 5x) | 4=
0
= 64/3 – 32 +20 =28/3(кв. ед.)
3.SADB = 20-28/3 = 32/3(кв.ед.).
Ответ:32/3.
Слайд 91. Скорость прямолинейного движения точки изменяется по закону
V(t)=3t²-2t.
Тогда закон движения
точки: S(t)=t³-2t²
2. Материальная точка движется со скоростью.
V(t)=sin t + cos t;
Уравнение движения
S (t) = cos t + sin t +C
Найти S (t), если при t =π/4, пройденный путь равен 3км
2. Материальная точка движется со скоростью.
V(t)=sin t + cos t;
Уравнение движения
S (t) = cos t + sin t +C
Найти S (t), если при t =π/4, пройденный путь равен 3км
«Поймай ошибку»
Слайд 11 Рефлексия. - Что понравилось на уроке? -
Какие задания вызывали затруднения?
- С каким настроением уходите с урока?
Всем спасибо!