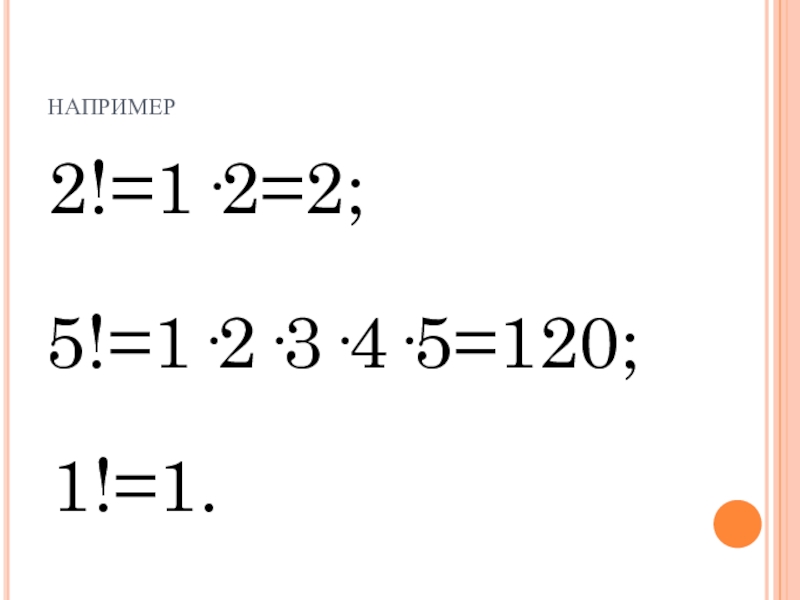Ю.Н. Макарычев
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Перестановки (9 класс)
Содержание
- 1. Презентация по алгебре на тему Перестановки (9 класс)
- 2. Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
- 3. Например Пусть имеются три книги. Обозначим их
- 4. Если первой поставить книгу а, то возможны такие расположения книг:abcabc
- 5. Если первой поставить книгу в, то возможны такие расположения книг:abcabc
- 6. Если первой поставить книгу с, то возможны такие расположения книг:abcabc
- 7. Каждое из этих расположений называют перестановкой из
- 8. Число перестановок из n элементов Обозначатся символомЧитается
- 9. Воспользуемся комбинаторным правилом умноженияНа первое место можно
- 10. Формула числа перестановок из n элементов
- 11. Для произведения первых n натуральных чисел используетсяобозначениечитается
- 12. например2!=1·2=2;5!=1·2·3·4·5=120;1!=1.
- 13. Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках?Задача 1Решение Ответ: 40320.
- 14. Сколько различных четырехзначных чисел, в которых цифры
- 15. Имеется девять различных книг, четыре из которых
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Слайд 1перестановки
Легомина Виктория Сергеевна, учитель математики МБОУ Первомайской СОШ.
Учебник. Алгебра, 9 класс.
Слайд 2Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Слайд 3Например
Пусть имеются три книги. Обозначим их буквами а, b и
с. Эти книги можно поставить на полке по-разному.
a
b
c
Слайд 7Каждое из этих расположений называют перестановкой из трех элементов
Перестановкой из n
элементов называют каждое расположение этих элементов в определенном порядке.
Слайд 9Воспользуемся комбинаторным правилом умножения
На первое место можно поставить любой из трех
элементов.
Для каждого выбора первого элемента есть две возможности выбора второго из оставшихся двух элементов.
Для каждого выбора первых двух элементов есть единственная возможность выбора третьего элемента.
Для каждого выбора первого элемента есть две возможности выбора второго из оставшихся двух элементов.
Для каждого выбора первых двух элементов есть единственная возможность выбора третьего элемента.
Слайд 13Сколькими способами можно расставить 8 участниц финального забега на восьми беговых
дорожках?
Задача 1
Решение
Ответ: 40320.
Слайд 14Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить
из цифр 0, 2, 4, 6?
Задача 2
Решение
Ответ: 18.
Слайд 15Имеется девять различных книг, четыре из которых – учебники. Сколькими способами
можно расставить эти книги на полке так, чтобы все учебники стояли рядом?
Задача 3
Решение
Ответ: 17280.