Светлана Николаевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Множества чисел
Содержание
- 1. Презентация по алгебре на тему Множества чисел
- 2. Координатный луч01234
- 3. Множество натуральных чисел N (числа, которые используют для счета предметов)3412
- 4. Добавив к ним число 0 и противоположные числа, получили множество целых чисел Z
- 5. Добавив к ним все дробные числа, получили
- 6. Целые и дробные числа образуют множество
- 7. Из истории возникновения рациональных чисел: В
- 8. Решая уравнение х²=2, мы получаем корни
- 9. Вывод: все числа, с которыми мы знакомы,
Координатный луч01234
Слайд 5Добавив к ним все дробные числа, получили множество рациональных чисел Q
½
0
1
2
-1
0,5
-2
-2,1
1,8
-
Слайд 6
Целые и дробные числа образуют множество рациональных чисел Q
Число,
которое можно записать в виде отношения , где а є Z, а n є N, называют рациональным числом
8 = ; -6= ; 0= ; - = ;
- 4 =
8 = ; -6= ; 0= ; - = ;
- 4 =
Слайд 7Из истории возникновения рациональных чисел:
В жизни люди «открывали» рациональные
числа постепенно. Вначале возникли натуральные числа. Первыми были 1 и 2. Долго не было других числительных. Вместо «3» говорили «один-два», вместо 4 «два-два».И так до шести. Потом шло «много».
С дробями люди столкнулись при разделе добычи. Для облегчения работы с дробями были придуманы десятичные дроби. В Европе их ввел в 1585 году голландский математик Симон Стевин.
С дробями люди столкнулись при разделе добычи. Для облегчения работы с дробями были придуманы десятичные дроби. В Европе их ввел в 1585 году голландский математик Симон Стевин.
Слайд 8Решая уравнение х²=2, мы получаем корни и -
. Эти числа не являются рациональными, т.к. не существует числа квадрат которого равен 2
=1, 414213562373095048… -
бесконечная непериодическая десятичная дробь. Такие числа наз.
иррациональными
примеры: π ≈ 3,14, ℮ ≈ 2,7
Слайд 9
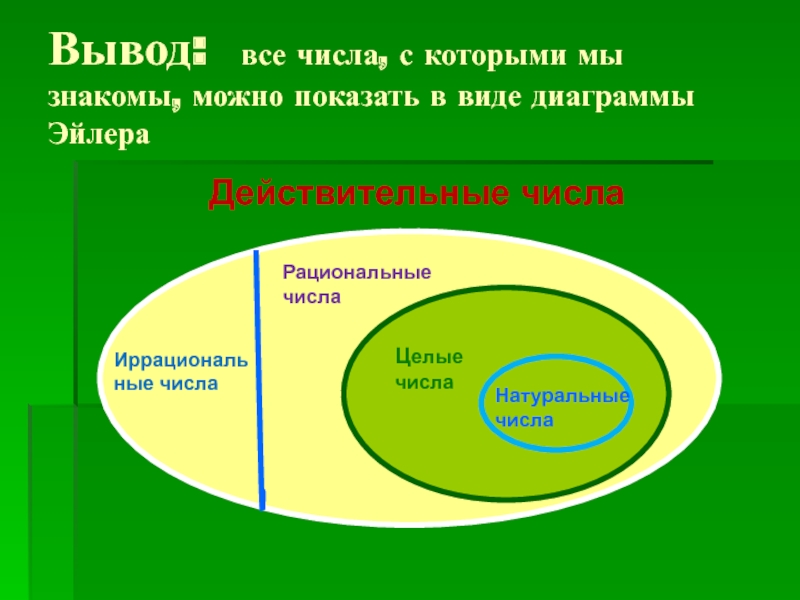
Вывод: все числа, с которыми мы знакомы, можно показать в виде
диаграммы Эйлера
Действительные числа
Натуральные числа
Целые числа
Рациональные числа
Иррациональные числа