- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему : Логарифмическая функция (11 класс).
Содержание
- 1. Презентация по алгебре на тему : Логарифмическая функция (11 класс).
- 2. Логарифмическая функцияФункцию заданную формулой y=log a xназывают логарифмической функцией с основанием a. а>0, a≠1Определение:
- 3. Свойства логарифмической функцииСвойство 1°:Область определения логарифмической функции
- 4. Свойства логарифмической функцииСвойство 2°:Область значения логарифмической функции
- 5. Свойства логарифмической функции Доказательство: Докажем что
- 6. Определите какая из перечисленных функций является убывающей, а какая возрастающей?
- 7. Сравните числа
- 8. Ответы:
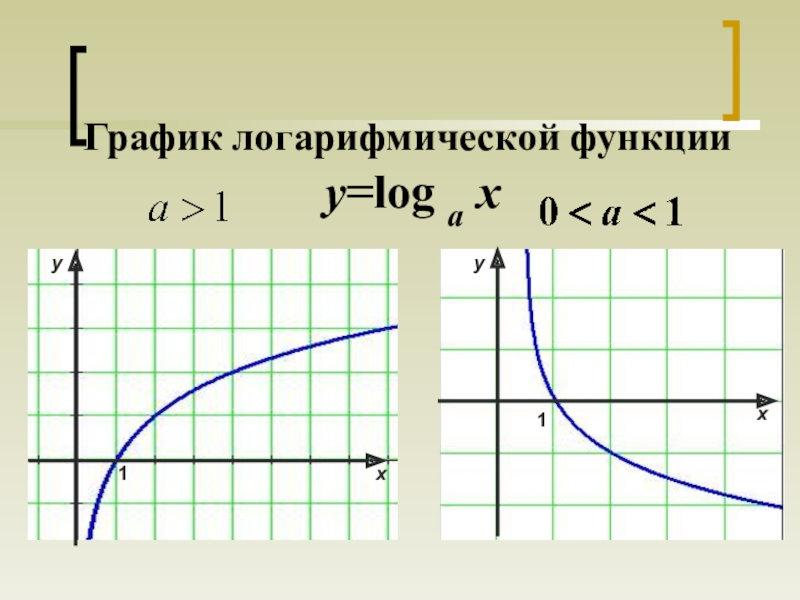
- 9. График логарифмической функции y=log a x11yyxx
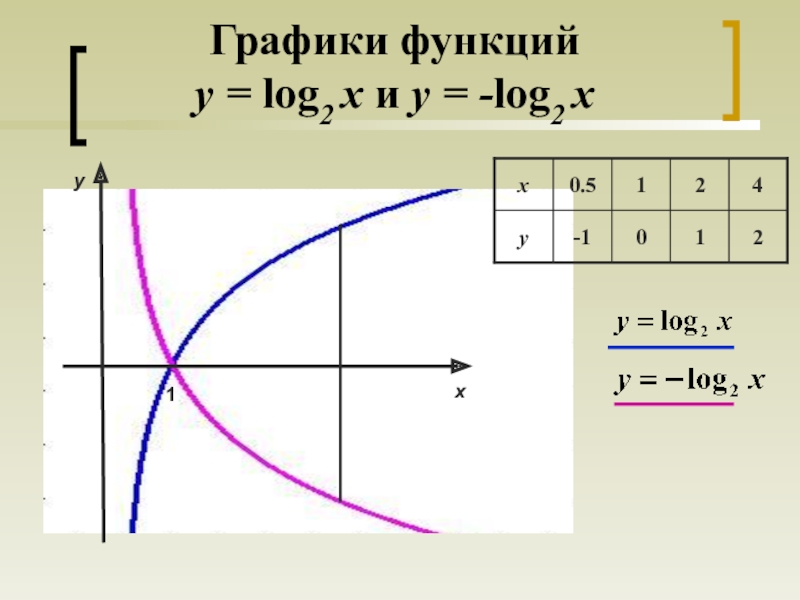
- 10. Графики функций y = log2 x и y = -log2 x 1yх
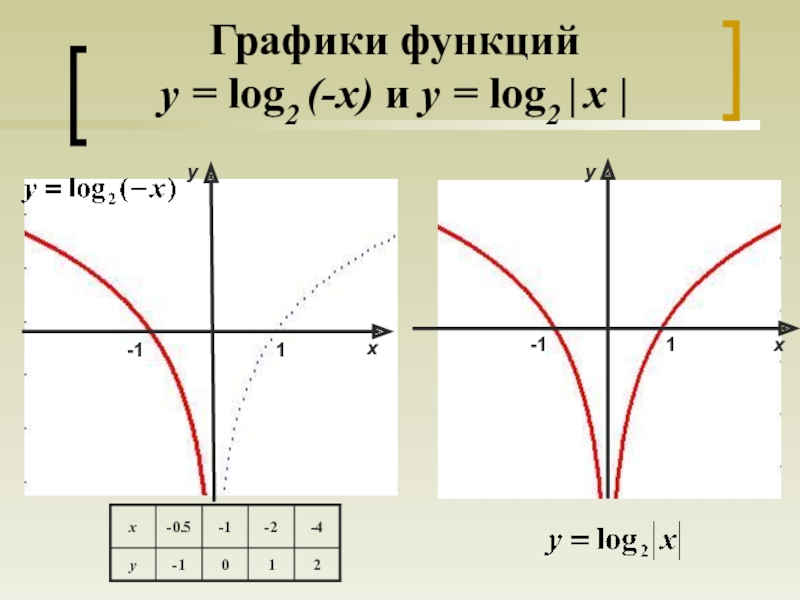
- 11. Графики функций y = log2 (-x) и y = log2 | x |1yх-1-1yх1
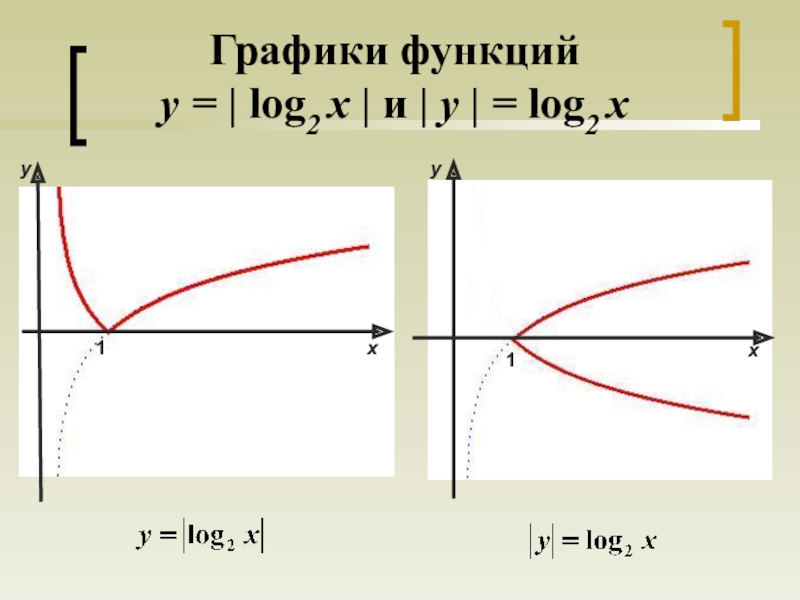
- 12. Графики функций y = | log2
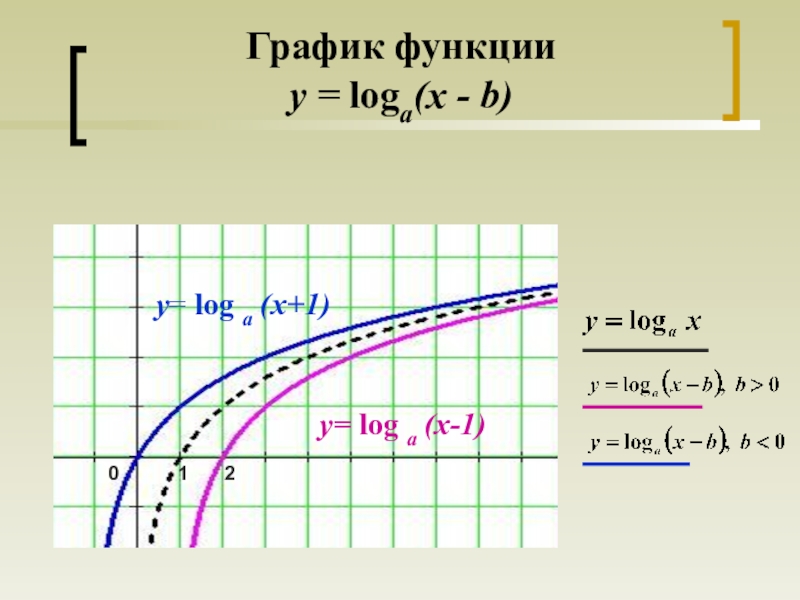
- 13. y= log a (x+1)y= log a (x-1)График функции y = loga(x - b)120
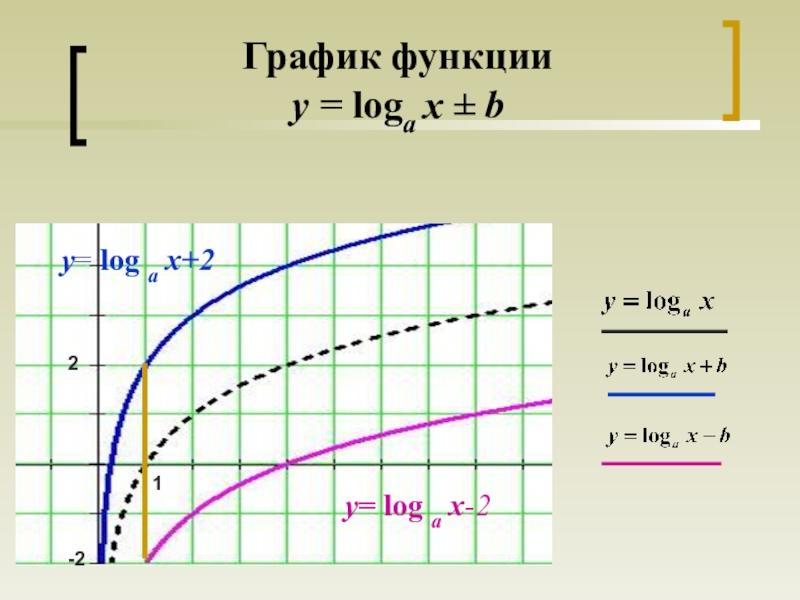
- 14. y= log a x+2y= log a x-2График функции y = loga x ± b2-21
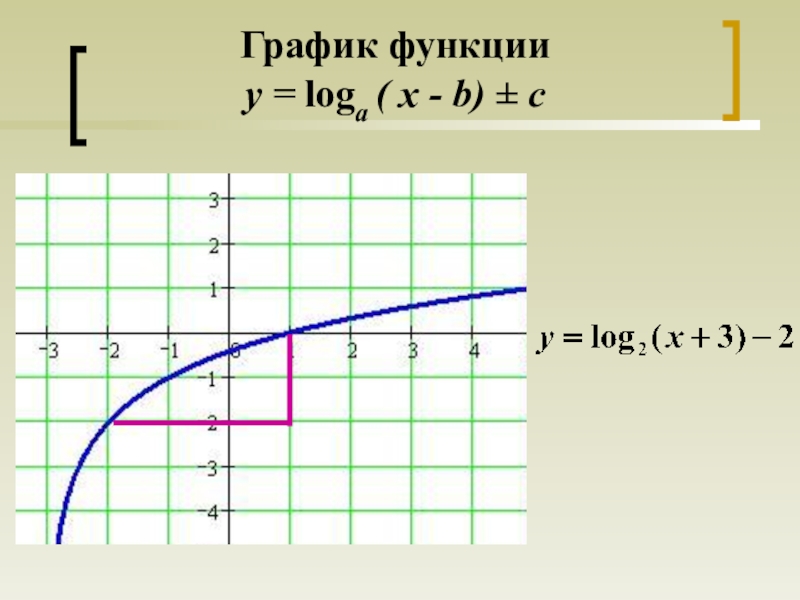
- 15. График функции y = loga ( x - b) ± c
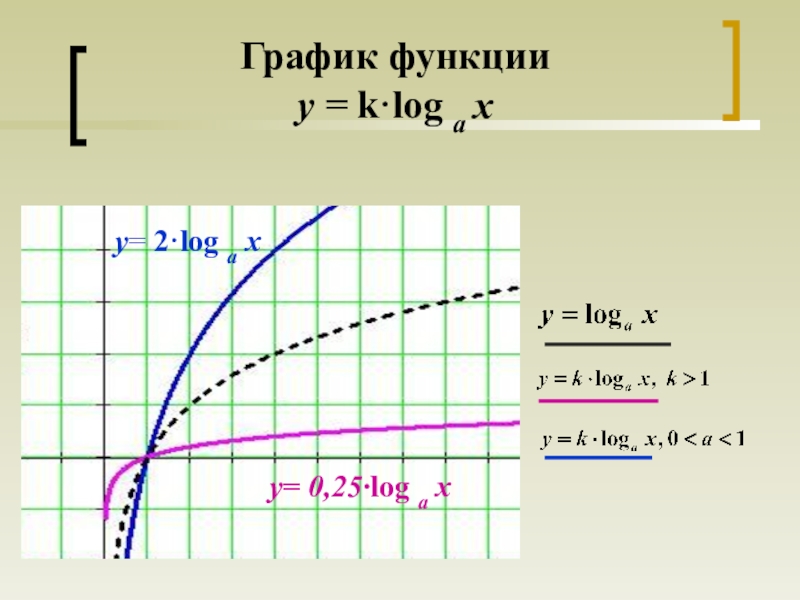
- 16. График функции y = k·log a x y= 2·log a xy= 0,25·log a x
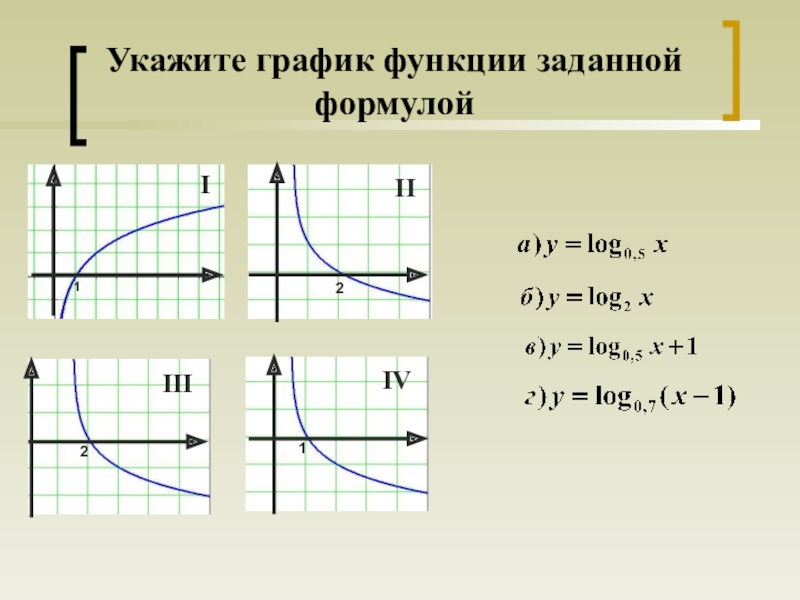
- 17. Укажите график функции заданной формулой1221IIIIVIII
- 18. Пример 1Найти область определения функции f(x)=log8 (4-5x)Решение:Область
- 19. Пример 2Найти область определения функции f(x) =
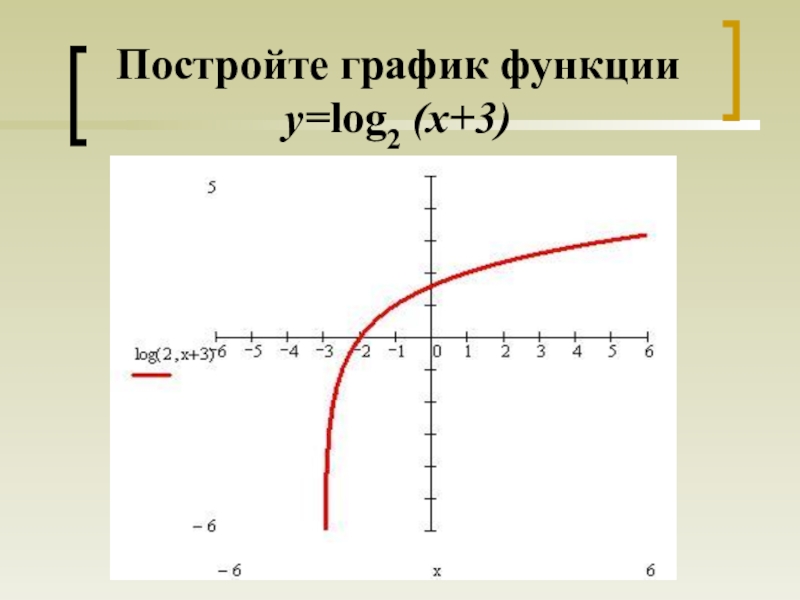
- 20. Постройте график функции y=log2 (x+3)
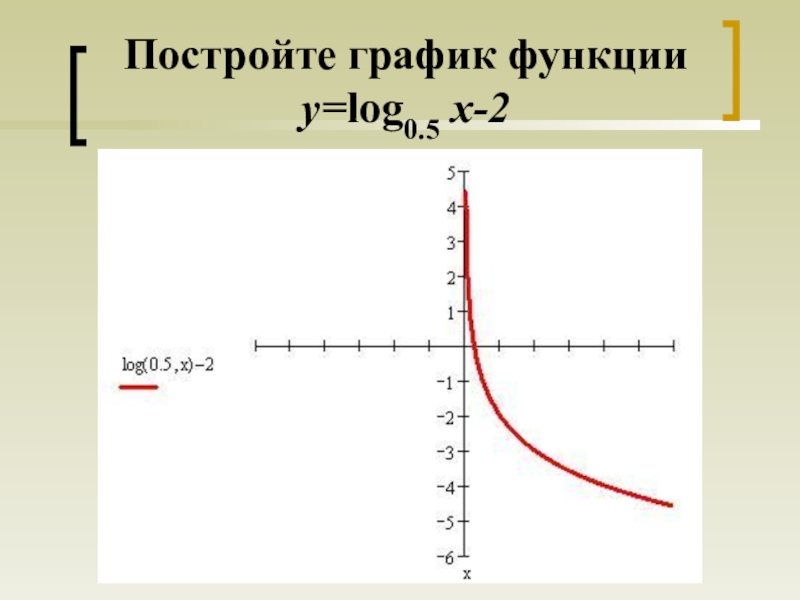
- 21. Постройте график функции y=log0.5 x-2
- 22. Литература:Учебники «Алгебра и начала математического анализа», Алимов, 2012 г., Мордкович, 2012 г.Дидактические материалы для учителя.
Слайд 1Логарифмическая функция
Назарова Галина Алексеевна
учитель математики
ГБОУ Гимназия №1797
« Богородская»
г.
Слайд 2Логарифмическая функция
Функцию заданную формулой
y=log a x
называют логарифмической функцией с основанием
а>0, a≠1
Определение:
Слайд 3Свойства логарифмической функции
Свойство 1°:
Область определения логарифмической функции – множество всех положительный
Доказательство:
По определению логарифма
Слайд 4Свойства логарифмической функции
Свойство 2°:
Область значения логарифмической функции – множество всех действительных
E( log a )=R
Доказательство:
В самом деле, по определению логарифма любого действительного y справедливо равенство
т.е. функция y=log a x принимает значение y0 в точке
Слайд 5Свойства логарифмической функции
Доказательство:
Докажем что при a > 1функция возрастает (в случае
Свойство 3°:
Логарифмическая функция на всей области определения возрастает (при а>1)
убывает (при 0
Слайд 18Пример 1
Найти область определения функции
f(x)=log8 (4-5x)
Решение:
Область определения логарифмической функции –
Ответ: ( -∞ ; 0,8 )
Слайд 19Пример 2
Найти область определения функции
f(x) = log0,3 ( x-x2 )
Решение:
Функция
Ответ: ( 0;1 )
Слайд 22Литература:
Учебники «Алгебра и начала математического анализа», Алимов, 2012 г., Мордкович, 2012
Дидактические материалы для учителя.