- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Линейные у
Содержание
- 1. Презентация по алгебре на тему Линейные у
- 2. Линейные уравнения с двумя переменнымицельДать определение линейного
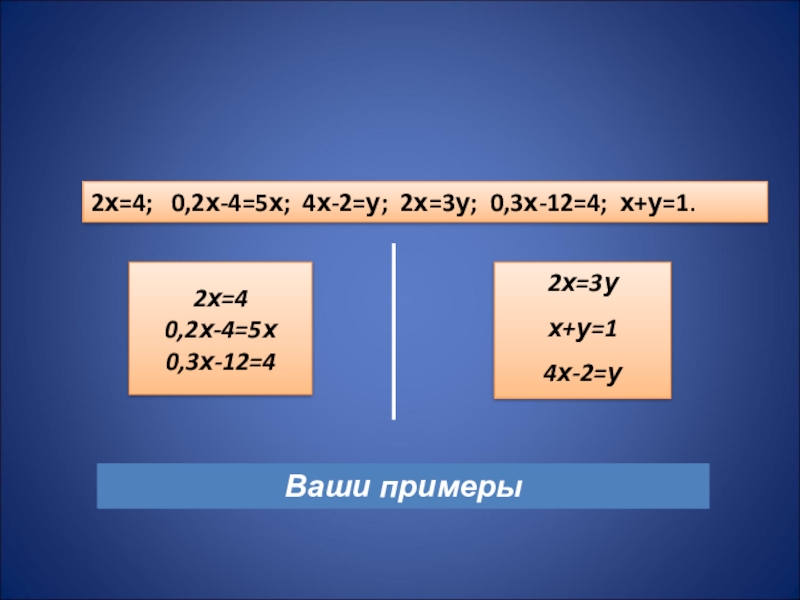
- 3. 2х=4; 0,2х-4=5х; 4х-2=у; 2х=3у; 0,3х-12=4; х+у=1.2х=40,2х-4=5х0,3х-12=42х=3ух+у=14х-2=уВаши примеры
- 4. Определение линейного уравнения с двумя переменнымиЛинейным уравнением
- 5. Подберём решение уравнений2х+у=5Подберем пары чисел, которые обратят
- 6. Найдём пары чисел, которые являются решением уравнений.Для
- 7. Попробуй выразить:а) у через хб) х через
- 8. Какими преобразованиями мы пользовались?а) переносили слагаемые из
- 9. Знаем определение линейного уравнения с двумя переменными.Умеем
- 10. Используемая литератураУчебник АЛГЕБРА -7 под ред.С.А.
Слайд 2Линейные уравнения с двумя переменными
цель
Дать определение линейного уравнения с двумя переменными
Выяснить,
Рассмотреть свойства уравнений
Слайд 32х=4; 0,2х-4=5х; 4х-2=у; 2х=3у; 0,3х-12=4; х+у=1.
2х=4
0,2х-4=5х
0,3х-12=4
2х=3у
х+у=1
4х-2=у
Ваши примеры
Слайд 4Определение линейного уравнения
с двумя переменными
Линейным уравнением с двумя переменными называется
вида ах+ву=с, где х и у – переменные, а, в, с- некоторые числа.
Проверь себя
7-х=у; 5х-у=4; 2ху+5=х; 2х-0,4у+7=6; х=ху+8; у- 4х+2у=7
ДА
Слайд 5
Подберём решение уравнений
2х+у=5
Подберем пары чисел, которые обратят данное
уравнение в верное
Если х=1,то у=3
Если х=2, то у=1
Если х=0, тоу=5
Т.к при подстановке этих
значений переменных в
данное уравнение полу-
чается верное равенство.
Попробуем выразить одну переменную через другую
2х+у=5 у=5-2х или х =
Слайд 6Найдём пары чисел, которые являются
решением уравнений.
Для этого:
выразим одну переменную
придадим значение одной переменной
вычислим значение другой переменной
3х=7+7у
Х=
если у=0, то х =
если у=2, то х=7
если у=-1, то х=0.
Мы получили решения линейного уравнения с двумя
переменными.
Они записываются парой
чисел.
Слайд 7Попробуй выразить:
а) у через х
б) х через у
у-2х=4
2х-у=5
0,5х+2у=8
7у=3х
Х=
Х=16-4у
Х=
У=4+2х
У=
Х=
У=2х-5
У=
Слайд 8
Какими преобразованиями мы пользовались?
а) переносили слагаемые из одной части в другую,
этом знак;
б)делили обе части уравнения на одно и то же число ,не равное
нулю
Найди пары решений уравнений
Х-у=2; х+у=8 ; у-6х=1.
Пусть х=0
(0;-2)
(0;8)
(0;1)
Какие из этих пар значений переменных являются
решением уравнения 2х+у=-5.
Слайд 9
Знаем определение линейного уравнения с двумя переменными.
Умеем выражать одну переменную через
Умеем находить пары решений.
СПАСИБО ЗА УРОК
Слайд 10Используемая литература
Учебник АЛГЕБРА -7
под ред.С.А. Теляковского,
Москва, «Просвещение»
Алгебра. Самостоятельные разноуровневые работы.
Волгоград, «Учитель» 2006г.
Алгебраический тренажер 7
под ред.А.Г. Мордковича.
Москва «Новый учебник» 2002г.