М. Никольского и др.
«Алгебра 8 класс»
Выполнила: учитель математики
МБОУ Сатисской СОШ Интяпина Е.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Квадратные уравнения
Содержание
- 1. Презентация по алгебре на тему Квадратные уравнения
- 2. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
- 3. Слайд 3
- 4. Познавательные:-формирование представлений о полном, приведённом, неполном квадратном
- 5. РАЗВИВАЮЩИЕ:
- 6. ВОСПИТАТЕЛЬНЫЕ:
- 7. ОБОРУДОВАНИЕ И МАТЕРИАЛЫ:Медиапроектор .Презентация по теме «Квадратные
- 8. ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЕ ОБЪЯСНЕНИЕ СПЕЦИФИКИ ВОСПРИЯТИЯ И ОСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА УЧАЩИМИСЯ .
- 9. ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ УСВОЕНИЯ РАЗДЕЛА .Учащиеся 8 класса
- 10. МЕТОДЫ ОРГАНИЗАЦИИ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ. Информационно-развивающие :
- 11. Форма организации деятельности учащихся.Индивидуальные, групповые, фронтальные.Взаимного обучения, самообучения, саморазвитие.Массовые мероприятия: экскурсии, творческие отчёты, семинары.
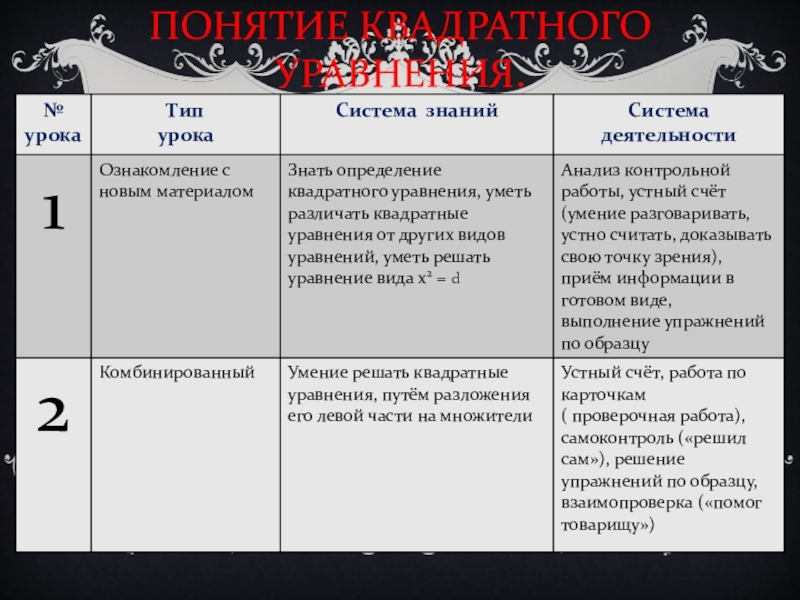
- 12. ПОНЯТИЕ КВАДРАТНОГО УРАВНЕНИЯ.
- 13. НЕПОЛНОЕ КВАДРАТНОЕ УРАВНЕНИЕ
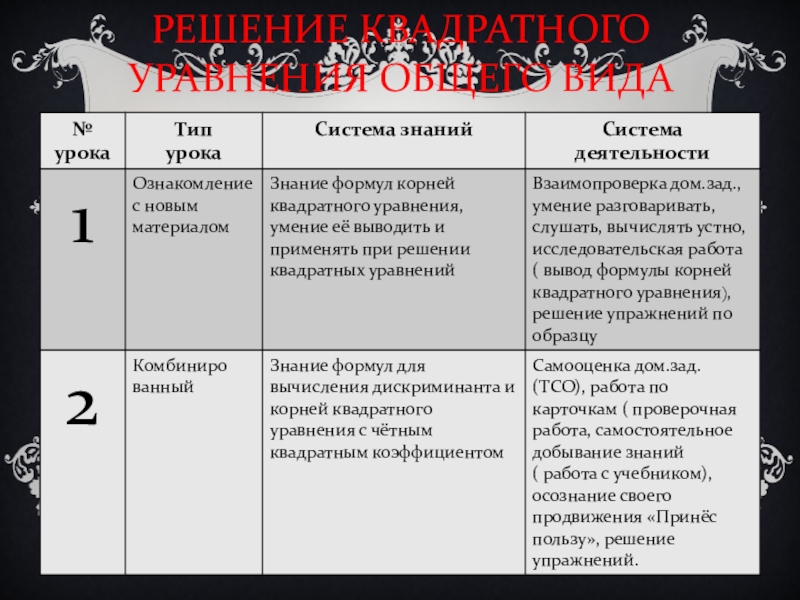
- 14. РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ОБЩЕГО ВИДА
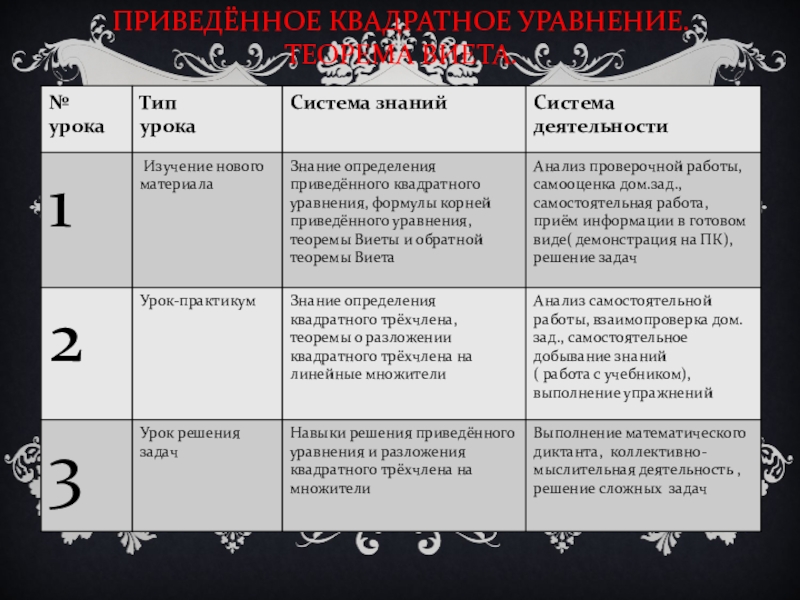
- 15. ПРИВЕДЁННОЕ КВАДРАТНОЕ УРАВНЕНИЕ. ТЕОРЕМА ВИЕТА.
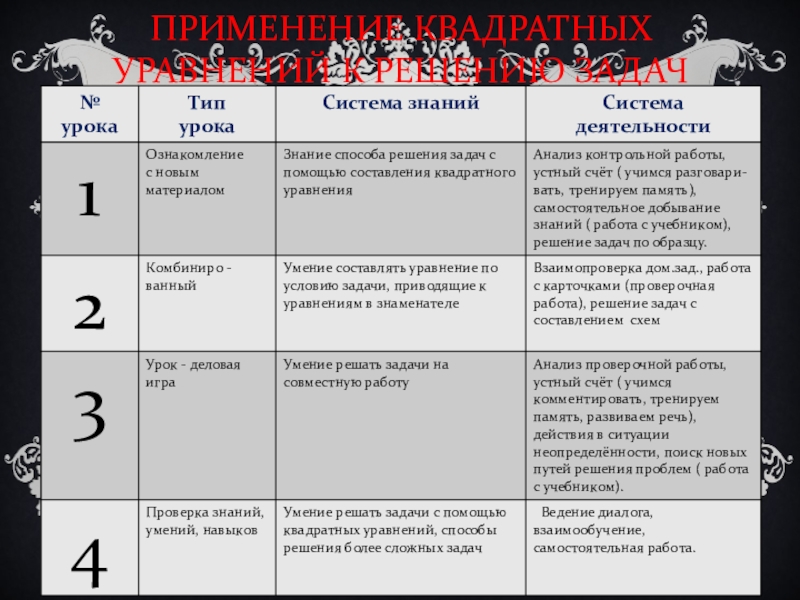
- 16. ПРИМЕНЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ К РЕШЕНИЮ ЗАДАЧ
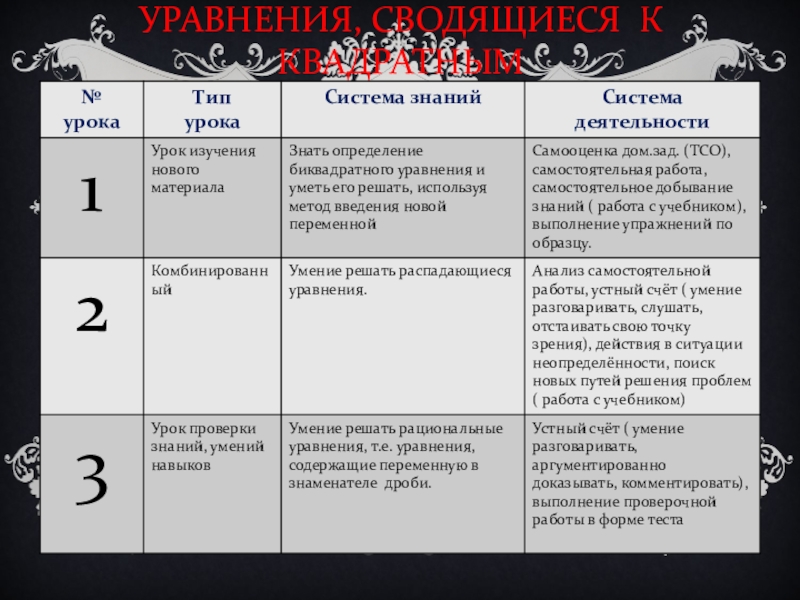
- 17. УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ
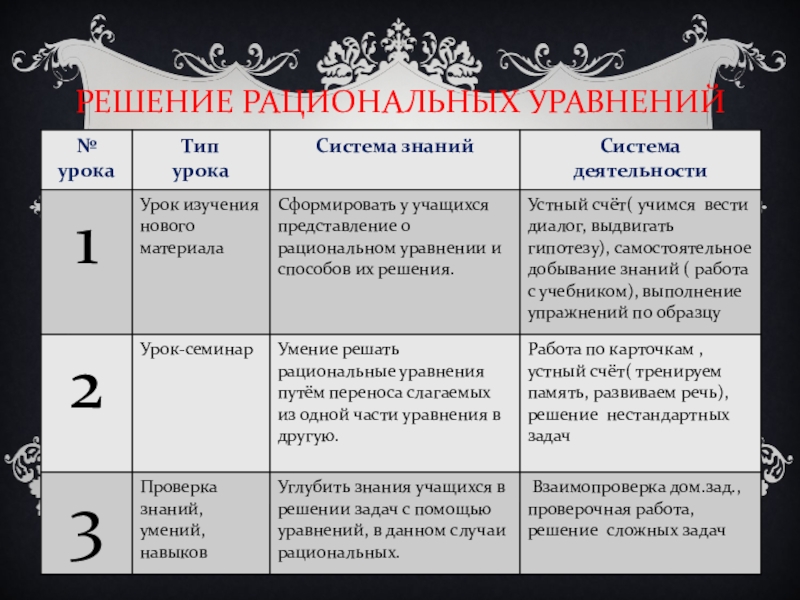
- 18. РЕШЕНИЕ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
- 19. ПОУРОЧНОЕ ПЛАНИРОВАНИЕ РАЗДЕЛА «КВАДРАТНЫЕ УРАВНЕНИЯ»
- 20. Слайд 20
- 21. РАЗРАБОТКА ОБОБЩАЮЩЕГО УРОКА ПО РАЗДЕЛУ «КВАДРАТНЫЕ
- 22. ЦЕЛИ УРОКА:
- 23. ОБОРУДОВАНИЕ И МАТЕРИАЛЫ:Медиапроектор .Презентация по теме «Квадратные
- 24. ПЛАН УРОКА
- 25. ВИДЫ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ НА КАЖДОМ ЭТАПЕ УРОКАI.Организационный
- 26. Оценочный листФамилия, имя _______________________
- 27. Если ты услышишь, что
- 28. ТЕОРЕТИЧЕСКАЯ РАЗМИНКА (10 МИН)Цель: повторение необходимых
- 29. ВОПРОСЫ ТЕОРЕТИЧЕСКОЙ РАЗМИНКИ: 1)Сформулируйте определение квадратного уравнения.2)Объясните,
- 30. уравнение вида ах2 + вх +с =
- 31. ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯНЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯКВАДРАТНЫЕ УРАВНЕНИЯа ≠
- 32. III.ГРУППОВАЯ РАБОТА ПО КАРТОЧКАМ (7 МИН)Цель:
- 33. КАРТОЧКА №1:
- 34. КАРТОЧКА №2:Определи вид квадратного уравнения:
- 35. КАРТОЧКА №3:Определите коэффициенты квадратного уравнения: а) 6х2
- 36. а) 6х2 – х + 4 =
- 37. IV.СОВМЕСТНАЯ РАБОТА УЧИТЕЛЯ С КЛАССОМ (15 МИН)Цель
- 38. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0 1.Перенос с
- 39. РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ :1 вариант:
- 40. Способы решения полных квадратных уравненийВыделение квадрата двучлена.2.Формула: D = b2- 4ac, x1,2=3.Теорема Виета.
- 41. РЕШИ УРАВНЕНИЯ способом выделения квадрата двучлена :1
- 42. РЕШИ УРАВНЕНИЯ с помощью формулы :1 вариант:
- 43. КАРТОЧКА №4:Реши уравнения с помощью теоремы Виета: 1.
- 44. V.ИСТОРИЧЕСКИЕ СВЕДЕНИЯ(7 МИН)Цель: формирование учебно-познавательной мотивации школьников
- 45. ФРАНСУА ВИЕТ
- 46. Испанский математик Вальмес в 1486 году
- 47. Однажды французам удалось перехватить приказы испанского правительства
- 48. Теорема Виета
- 49. Исторические сведения:Квадратные уравнения впервые встречаются в работе
- 50. Решение задачи Бхаскары:Пусть было x
- 51. VI.ПОДВЕДЕНИЕ ИТОГОВ УРОКА (2 МИН)Цель:
- 52. Оценочный лист
- 53. Оценочный листФамилия, имя Биричева Т. Забродина Н. Климова А. Сёмина А. Пунина Н.
- 54. Оценочный листФамилия, имя Москвина Г. Шуваев М. Смыслова О. Буланкина В Маркин А.
- 55. VII.ДОМАШНЕЕ ЗАДАНИЕ (2 МИН)Цель: подготовиться к контрольной
- 56. СПИСОК ЛИТЕРАТУРЫ1. Бурмистрова Т.А. Программы ОУ. Алгебра
- 57. Спасибо за внимание!
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Слайд 1МЕТОДИЧЕСКАЯ РАЗРАБОТКА
РАЗДЕЛА АЛГЕБРЫ 8 КЛАССА «КВАДРАТНЫЕ УРАВНЕНИЯ»
Учебник под редакцией С.
Слайд 4Познавательные:
-формирование представлений о полном, приведённом, неполном квадратном уравнении, о дискриминанте, о
формулах корней квадратного уравнения, о теореме Виета;
- Овладение умением разложения квадратного трёхчлена на множители, решения квадратного уравнения по соответствующим формулам;
-формирование умений решать уравнения, сводящиеся к квадратным;
-овладение методами решения систем, содержащих уравнения второй степени.
-формирование устойчивых навыков в решении задач с помощью квадратных уравнений.
- Овладение умением разложения квадратного трёхчлена на множители, решения квадратного уравнения по соответствующим формулам;
-формирование умений решать уравнения, сводящиеся к квадратным;
-овладение методами решения систем, содержащих уравнения второй степени.
-формирование устойчивых навыков в решении задач с помощью квадратных уравнений.
Слайд 7ОБОРУДОВАНИЕ И МАТЕРИАЛЫ:
Медиапроектор .
Презентация по теме «Квадратные уравнения».
Контрольная работа № 3,
№ 4.
Самостоятельные работы по темам: «Теорема Виета», «Рациональные уравнения», «Решение задач».
Оценочный лист для контроля и самоконтроля.
Карточки-задания для устной и
индивидуальной работы.
Самостоятельные работы по темам: «Теорема Виета», «Рациональные уравнения», «Решение задач».
Оценочный лист для контроля и самоконтроля.
Карточки-задания для устной и
индивидуальной работы.
Слайд 8ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЕ ОБЪЯСНЕНИЕ СПЕЦИФИКИ ВОСПРИЯТИЯ И ОСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА УЧАЩИМИСЯ .
Слайд 9ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ УСВОЕНИЯ РАЗДЕЛА .
Учащиеся 8 класса должны:
уметь решать квадратные
уравнения, системы уравнений, содержащие уравнения второй степени, задачи с помощью квадратных уравнений;
совершенствовать математическую речь;
применять полученные знания при моделировании практических задач;
совершенствовать математическую речь;
применять полученные знания при моделировании практических задач;
Слайд 10МЕТОДЫ ОРГАНИЗАЦИИ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ.
Информационно-развивающие : передача информации в готовом
виде (объяснение, демонстрация презентаций), самостоятельное добывание знаний
(самостоятельная работа с книгой, использование информационных технологий).
Проблемно-поисковые: эвристическая беседа, учебная дискуссия, организация коллективной мыслительной деятельности, исследовательская работа.
Репродуктивные : пересказ учебного материала, выполнение упражнений по образцу.
Творчески – репродуктивные: вариативные упражнения, анализ учебной ситуации.
(самостоятельная работа с книгой, использование информационных технологий).
Проблемно-поисковые: эвристическая беседа, учебная дискуссия, организация коллективной мыслительной деятельности, исследовательская работа.
Репродуктивные : пересказ учебного материала, выполнение упражнений по образцу.
Творчески – репродуктивные: вариативные упражнения, анализ учебной ситуации.
Слайд 11Форма организации деятельности учащихся.
Индивидуальные,
групповые,
фронтальные.
Взаимного обучения,
самообучения,
саморазвитие.
Массовые
мероприятия:
экскурсии,
творческие отчёты,
семинары.
Слайд 21РАЗРАБОТКА ОБОБЩАЮЩЕГО УРОКА ПО РАЗДЕЛУ
«КВАДРАТНЫЕ УРАВНЕНИЯ»
Тема урока: обобщение изученного
материала по теме «Квадратные уравнения»
Класс: 8
Дата проведения: 05.12.2012 года.
Тип урока: систематизация
и обобщение изученного
материала
Класс: 8
Дата проведения: 05.12.2012 года.
Тип урока: систематизация
и обобщение изученного
материала
Слайд 23ОБОРУДОВАНИЕ И МАТЕРИАЛЫ:
Медиапроектор .
Презентация по теме «Квадратные уравнения».
Оценочный лист для контроля
и самоконтроля.
Карточки-задания для устной и
индивидуальной работы.
Карточки-задания для устной и
индивидуальной работы.
Слайд 25ВИДЫ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ НА КАЖДОМ ЭТАПЕ УРОКА
I.Организационный момент (2 мин)
Цель:
формирование мотива, желания работать на уроке.
См.приложение к уроку – «Оценочный лист»
См.презентацию «Квадратные уравнения», слайд 2
Учащиеся записывают дату и тему урока.
См.приложение к уроку – «Оценочный лист»
См.презентацию «Квадратные уравнения», слайд 2
Учащиеся записывают дату и тему урока.
Слайд 27 Если ты услышишь, что кто-то не любит математику,
не верь.
Её нельзя не любить - её можно только не знать.
Её нельзя не любить - её можно только не знать.
Слайд 28 ТЕОРЕТИЧЕСКАЯ РАЗМИНКА
(10 МИН)
Цель: повторение необходимых теоретических сведений по теме, развитие
умения говорить и слушать.
См.приложение к уроку – «Вопросы теоретической разминки»
См. Презентация «Квадратные уравнения» слайд 3,Слайд 4
Учащиеся получают возможность говорить, отвечать, проверять, оценивать.
См.приложение к уроку – «Вопросы теоретической разминки»
См. Презентация «Квадратные уравнения» слайд 3,Слайд 4
Учащиеся получают возможность говорить, отвечать, проверять, оценивать.
Слайд 29ВОПРОСЫ ТЕОРЕТИЧЕСКОЙ РАЗМИНКИ:
1)Сформулируйте определение квадратного уравнения.
2)Объясните, в чем заключается смысл ограничения
в определении квадратного уравнения (а ≠ 0).
3)Перечислите виды квадратных уравнений.
4)Приведите примеры квадратных уравнений различных видов.
5)Какое квадратное уравнение называется приведенным? Приведите пример.
3)Перечислите виды квадратных уравнений.
4)Приведите примеры квадратных уравнений различных видов.
5)Какое квадратное уравнение называется приведенным? Приведите пример.
Слайд 30
уравнение вида ах2 + вх +с = 0,
где х
–переменная,
а, в и с некоторые числа,
причем а 0.
а, в и с некоторые числа,
причем а 0.
ОПРЕДЕЛЕНИЕ:
Квадратным уравнением называется
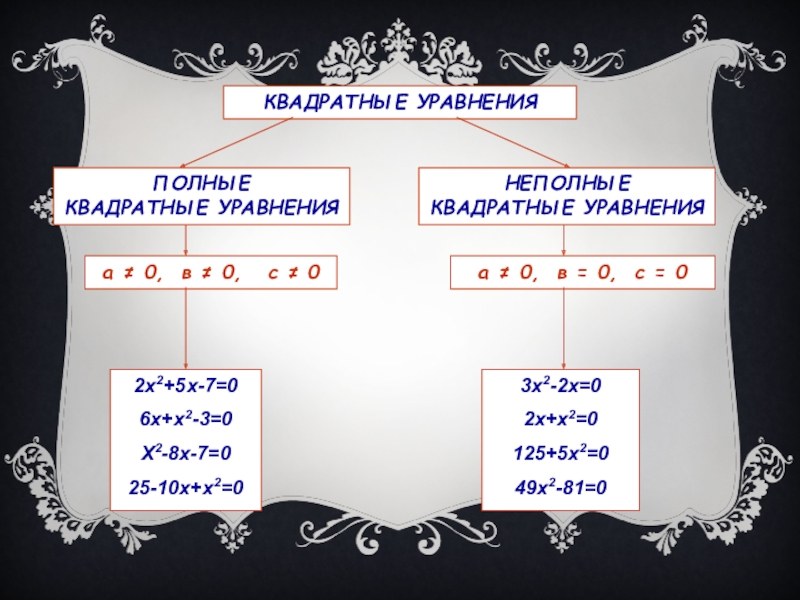
Слайд 31ПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
НЕПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в ≠ 0, с
≠ 0
а ≠ 0, в = 0, с = 0
2х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0
3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0
Слайд 32III.ГРУППОВАЯ РАБОТА ПО КАРТОЧКАМ
(7 МИН)
Цель: проверка необходимых умений различать уравнения
среди других видов, определять вид квадратного уравнения и его коэффициенты.
См.приложение к уроку – « карточка1, карточка2, карточка3»
См.презентацию «Квадратные уравнения», слайд 5
Учащиеся работают группами по карточкам (задания различного уровня сложности)
См.приложение к уроку – « карточка1, карточка2, карточка3»
См.презентацию «Квадратные уравнения», слайд 5
Учащиеся работают группами по карточкам (задания различного уровня сложности)
Слайд 34КАРТОЧКА №2:
Определи вид квадратного уравнения:
а)
1,3х2 = 4 б) 3х2 = 0
в) (х-3)(х-5) = 2х г) (12х-3)(х-5) = 2х
д)
в) (х-3)(х-5) = 2х г) (12х-3)(х-5) = 2х
д)
Слайд 35КАРТОЧКА №3:
Определите коэффициенты квадратного уравнения:
а) 6х2 – х + 4
= 0 б) 12х - х2 + 7 = 0
в) 8 + 5х2 = 0 г) х – 6х2 = 0
д) - х + х2 = 15
в) 8 + 5х2 = 0 г) х – 6х2 = 0
д) - х + х2 = 15
Слайд 36а) 6х2 – х + 4 = 0
б) 12х - х2
+ 7 = 0
в) 8 + 5х2 = 0
г) х – 6х2 = 0
д) - х + х2 = 15
в) 8 + 5х2 = 0
г) х – 6х2 = 0
д) - х + х2 = 15
а = 6, в = -1, с = 4;
а = -1, в = 12, с = 7;
а = 5, в = 0, с = 8;
а = -6, в =1, с = 0;
а = 1, в =-1, с = -15.
Определите коэффициенты
квадратного уравнения:
Слайд 37IV.СОВМЕСТНАЯ РАБОТА УЧИТЕЛЯ С КЛАССОМ
(15 МИН)
Цель : повторение способов решения:
а)неполных квадратных
уравнений,
б)полных квадратных уравнений.
См.презентацию «Квадратные уравнения», слайд 6-11
См.приложение к уроку – «Карточка 4»
Учащиеся отвечают, решают уравнения, оценивают себя.
б)полных квадратных уравнений.
См.презентацию «Квадратные уравнения», слайд 6-11
См.приложение к уроку – «Карточка 4»
Учащиеся отвечают, решают уравнения, оценивают себя.
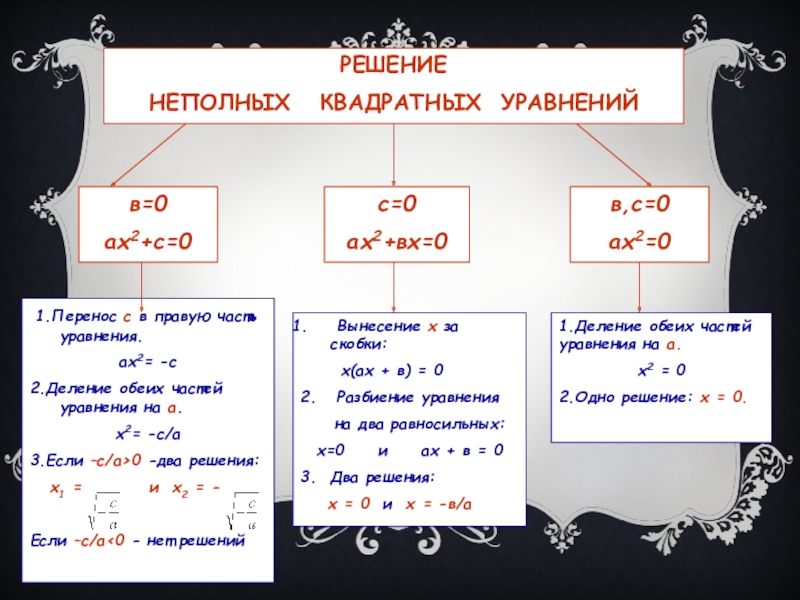
Слайд 38РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах2+с=0
с=0
ах2+вх=0
в,с=0
ах2=0
1.Перенос с в правую часть уравнения.
ах2=
-с
2.Деление обеих частей уравнения на а.
х2= -с/а
3.Если –с/а>0 -два решения:
х1 = и х2 = -
Если –с/а<0 - нет решений
2.Деление обеих частей уравнения на а.
х2= -с/а
3.Если –с/а>0 -два решения:
х1 = и х2 = -
Если –с/а<0 - нет решений
Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.
Слайд 39
РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ :
1 вариант:
а)
б) ( х + 2)2 + ( х -3)2 = 13
2 вариант:
а) 2х + х2= 0
б) 49х2 – 81 = 0
3 вариант:
а) 3х2 – 2х = 0
б) 125 + 5х2 = 0
б) ( х + 2)2 + ( х -3)2 = 13
2 вариант:
а) 2х + х2= 0
б) 49х2 – 81 = 0
3 вариант:
а) 3х2 – 2х = 0
б) 125 + 5х2 = 0
Слайд 40Способы решения
полных квадратных уравнений
Выделение квадрата двучлена.
2.Формула: D = b2- 4ac,
x1,2=
3.Теорема Виета.
3.Теорема Виета.
Слайд 41РЕШИ УРАВНЕНИЯ
способом выделения квадрата двучлена :
1 вариант: -
х + 3х2 – 70 =0
2 вариант: 2х2 -9х + 10 = 0
3 вариант: х2 – 8х -9 = 0
2 вариант: 2х2 -9х + 10 = 0
3 вариант: х2 – 8х -9 = 0
Слайд 42РЕШИ УРАВНЕНИЯ
с помощью формулы :
1 вариант: а) -7х +
5х2 + 1 =0
б) (х – 1)(х + 1) = 2 (5х – 10,5)
2 вариант: а) 2х2 + 5х -7 = 0
б) –х2 = 5х - 14
3 вариант: а) х2 – 8х + 7 = 0
б) 6х – 9 = х2
б) (х – 1)(х + 1) = 2 (5х – 10,5)
2 вариант: а) 2х2 + 5х -7 = 0
б) –х2 = 5х - 14
3 вариант: а) х2 – 8х + 7 = 0
б) 6х – 9 = х2
Слайд 43КАРТОЧКА №4:
Реши уравнения с помощью теоремы Виета:
1. х2 – 9х +
20 = 0
2. х2- 19х + 88 = 0
3. х2+ 16х + 63 = 0
4. В уравнении х2+ рх + 56 = 0 один из корней равен 7. Найди другой корень и коэффициент р.
2. х2- 19х + 88 = 0
3. х2+ 16х + 63 = 0
4. В уравнении х2+ рх + 56 = 0 один из корней равен 7. Найди другой корень и коэффициент р.
Слайд 44V.ИСТОРИЧЕСКИЕ СВЕДЕНИЯ(7 МИН)
Цель: формирование учебно-познавательной мотивации школьников на уроке, воспитание интереса
к предмету.
См.приложение к уроку – «Франсуа Виет»
См.презентацию «Квадратные уравнения», слайд 12,13
Учащиеся слушают, решают задачу Бхаскары.
См.приложение к уроку – «Франсуа Виет»
См.презентацию «Квадратные уравнения», слайд 12,13
Учащиеся слушают, решают задачу Бхаскары.
Слайд 45ФРАНСУА ВИЕТ
Жизнь Виета представляет для нас интерес во многих
отношениях. XV век в Западной Европе был веком ожесточенных религиозных волнений, и к началу XVI целый ряд стран отпал от католической церкви. Всесильная католическая церковь преследовала и убивала всякую мысль, в которой усматривала отклонение от своих учений. Церковный суд – инквизиция – всех попавшихся под подозрение карал вплоть до сожжения на костре, а имущество казненных отбирал в пользу церкви. Не один ученый погиб в руках инквизиции. В их числе были и математики.
Слайд 46
Испанский математик Вальмес в 1486 году как-то в семейном кругу
обмолвился о том, что нашел формулу для решения уравнения четвертой степени. В числе гостей оказался влиятельный инквизитор. Услышав слова Вальмеса, он заявил, что волей Божьей решать эти уравнения человеку не дано, а найти формулу можно было только с помощью дьявола.
В ту же ночь Вальмес был брошен в тюрьму, а через три недели сожжен на костре за связь с дьяволом. Лишь через 100 лет решение этих уравнений было найдено вторично.
Мэтр Виет также был на волосок от костра. В ту пору наиболее могущественное государство в Европе, Испания вела победоносную войну с Францией.
В ту же ночь Вальмес был брошен в тюрьму, а через три недели сожжен на костре за связь с дьяволом. Лишь через 100 лет решение этих уравнений было найдено вторично.
Мэтр Виет также был на волосок от костра. В ту пору наиболее могущественное государство в Европе, Испания вела победоносную войну с Францией.
Слайд 47Однажды французам удалось перехватить приказы испанского правительства командованию своих войск, написанные
очень сложным шифром (тайнописью). Виет с помощью математики сумел найти ключ к этому шифру. С этих пор французы, зная планы испанцев, с успехом предупреждали их наступления.
Инквизиция обвинила Виета в том, что он прибегнул к помощи дьявола, и приговорила к сожжению на костре. Но так как французы благодаря Виету в дальнейшем побеждали, он не был выдан инквизиции. В родном городке Виет был лучшим адвокатом, а позднее стал королевским советником. Но главным делом его жизни была математика. Биографы Виета пишут, что он мог несколько ночей подряд не спать, решая очередную математическую задачу.
Инквизиция обвинила Виета в том, что он прибегнул к помощи дьявола, и приговорила к сожжению на костре. Но так как французы благодаря Виету в дальнейшем побеждали, он не был выдан инквизиции. В родном городке Виет был лучшим адвокатом, а позднее стал королевским советником. Но главным делом его жизни была математика. Биографы Виета пишут, что он мог несколько ночей подряд не спать, решая очередную математическую задачу.
Слайд 49Исторические сведения:
Квадратные уравнения впервые встречаются в работе индийского математика и астронома
Ариабхатты.
Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
Слайд 50Решение задачи Бхаскары:
Пусть было x обезьянок,
тогда на поляне
забавлялось – .
Составим уравнение:
Составим уравнение:
+ 12 = х
Ответ: х1= 16 , х2= 48 обезьянок.
Слайд 51
VI.ПОДВЕДЕНИЕ ИТОГОВ УРОКА
(2 МИН)
Цель: подчеркнуть, что серьёзное отношение к теории помогает
углубить и расширить круг упражнений и задач по теме. Оценить работу учащихся на уроке.
Учащиеся слушают, подают дневники для выставления оценок.
Учащиеся слушают, подают дневники для выставления оценок.
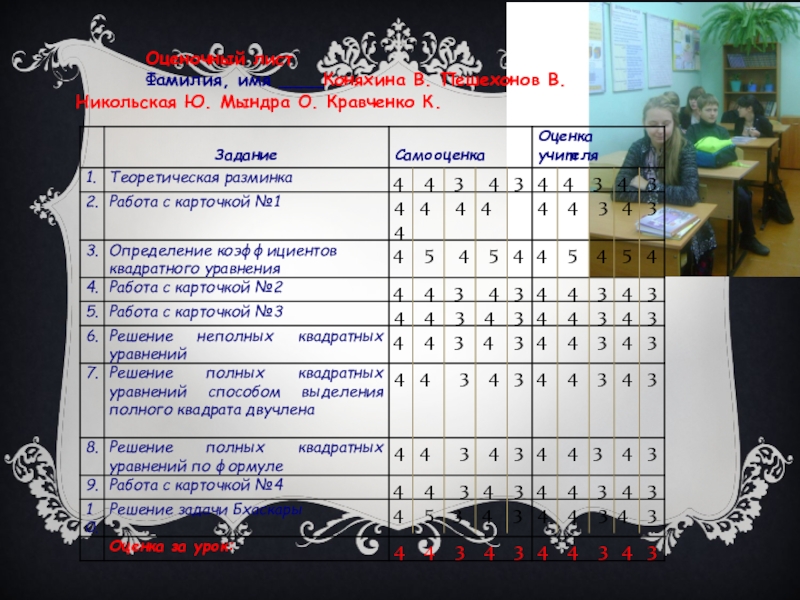
Слайд 52 Оценочный лист
Фамилия, имя ____Коняхина В. Пешехонов В.
Никольская Ю. Мындра О. Кравченко К.
Никольская Ю. Мындра О. Кравченко К.
Слайд 55VII.ДОМАШНЕЕ ЗАДАНИЕ (2 МИН)
Цель: подготовиться к контрольной работе
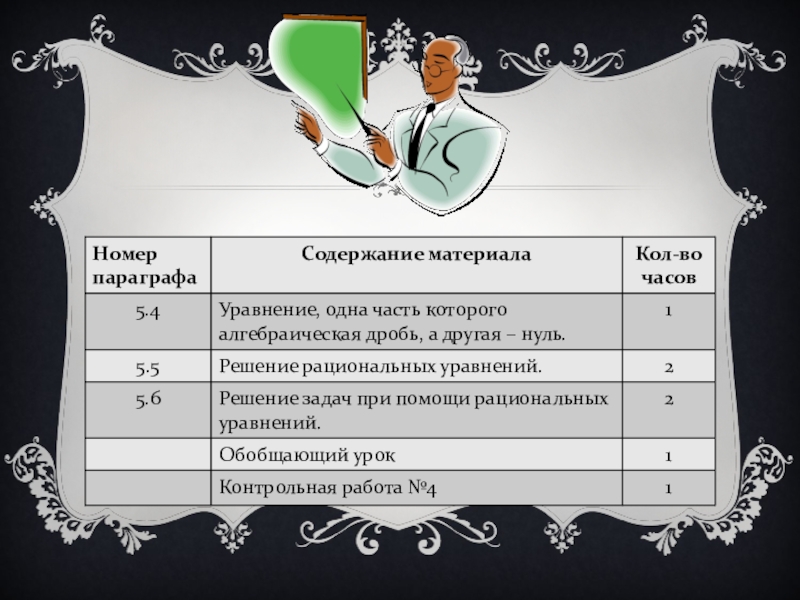
Повторить параграфы
5.1 –
5.6
Выполнить 371(д), 381(д),
385(а), 388(а).
Учащиеся записывают домашнее
задание в дневник.
Выполнить 371(д), 381(д),
385(а), 388(а).
Учащиеся записывают домашнее
задание в дневник.
Слайд 56СПИСОК ЛИТЕРАТУРЫ
1. Бурмистрова Т.А. Программы ОУ. Алгебра 7-9 классы. Москва «Просвещение»,2008
2.Никольский
С.М. и др. «Алгебра 8». Москва «Просвещение», 2010
3.Епишева О.Б. Общая методика преподавания математики в средней школе. Тобольск, Изд-во ТГПИ им.Д.И.Менделеева, 1997
4.Оганесян В.А. Методика преподавания математики в средней школе. Москва «Просвещение», 2003
5.Глейзер Г.И. История математики в школе 7-8 классы. Москва, 1982
6.Стефанова Н.Л. и др. Методика и технология обучения математике. Москва «Дрофа», 2005
7. Звавич Л.И. и др. Контрольные и проверочные работы по алгебре 7-9 классы. Москва «Прсвещение», 1996 г.
3.Епишева О.Б. Общая методика преподавания математики в средней школе. Тобольск, Изд-во ТГПИ им.Д.И.Менделеева, 1997
4.Оганесян В.А. Методика преподавания математики в средней школе. Москва «Просвещение», 2003
5.Глейзер Г.И. История математики в школе 7-8 классы. Москва, 1982
6.Стефанова Н.Л. и др. Методика и технология обучения математике. Москва «Дрофа», 2005
7. Звавич Л.И. и др. Контрольные и проверочные работы по алгебре 7-9 классы. Москва «Прсвещение», 1996 г.
