Боронилов,
МБОУ «Гимназия № 1», 8 «В» класс
Руководитель: Светлана Ивановна Яновская, учитель математики
г. Находка
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Извлечение квадратных корней из больших чисел без калькулятора.
Содержание
- 1. Презентация по алгебре на тему Извлечение квадратных корней из больших чисел без калькулятора.
- 2. Цель работы: найти и показать
- 3. Объект исследования: квадратные корни Предмет
- 4. Оглавление1. История квадратного корня2. Способ использования таблицы
- 5. История квадратного корня Арифметическим квадратным
- 6. Теорема о последней цифре квадрата числа Если
- 7. Способ использования таблицы квадратов двухзначных чисел Быстро,
- 8. Формула Древнего Вавилона (Вавилонский метод)Алгоритм извлечения
- 9. Слайд 9
- 10. Способ разложения на простые множители Для извлечения
- 11. Метод вычетов нечётного числа (арифметический способ) Суть
- 12. Метод подбора угадыванием (метод оценки)Рассмотрим пример извлечения
- 13. Метод отбрасывания полного квадрата Таким образом можно
- 14. Извлечение квадратного корня уголком6560
- 15. Практическая часть. Диаграммы анкетирования среди учащихся 8-11
- 16. Диаграмма № 2 - сложно ли Вам
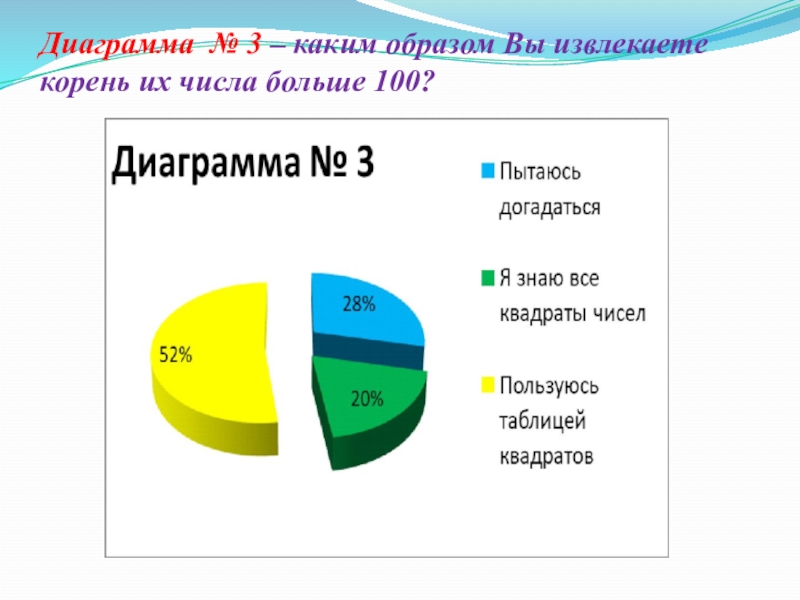
- 17. Диаграмма № 3 – каким образом Вы извлекаете корень их числа больше 100?
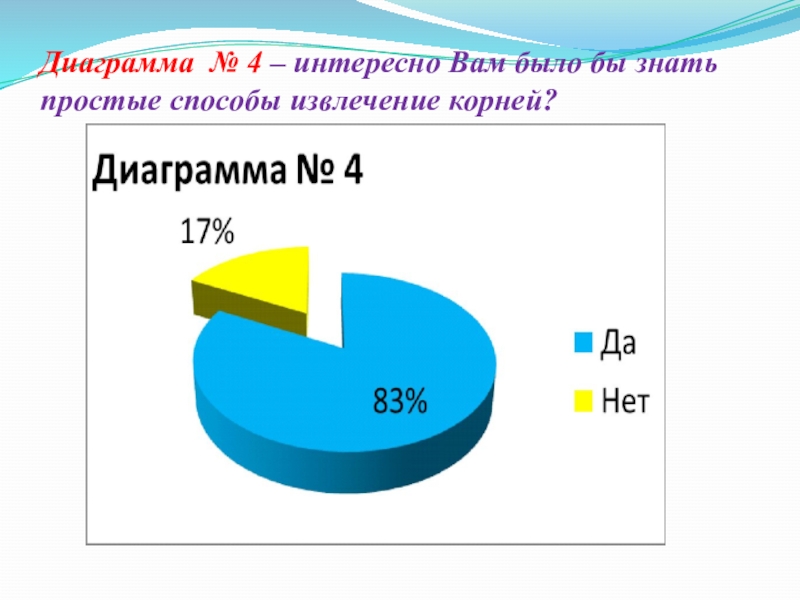
- 18. Диаграмма № 4 – интересно Вам было бы знать простые способы извлечение корней?
- 19. Заключение В ходе исследования было
- 20. Спасибо за внимание!
Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора. Задачи: - Изучить литературу по данному вопросу. - Рассмотреть особенности каждого найденного способа и
Слайд 2
Цель работы: найти и показать те способы извлечения
квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.
Задачи:
- Изучить литературу по данному вопросу.
- Рассмотреть особенности каждого найденного способа и его алгоритм.
- Показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов.
Задачи:
- Изучить литературу по данному вопросу.
- Рассмотреть особенности каждого найденного способа и его алгоритм.
- Показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов.
Слайд 3Объект исследования: квадратные корни
Предмет исследования: способы извлечения квадратных
корней без калькулятора.
Методы исследования:
Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.
Сравнение найденных способов.
Анализ полученных способов.
Методы исследования:
Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.
Сравнение найденных способов.
Анализ полученных способов.
Слайд 4Оглавление
1. История квадратного корня
2. Способ использования таблицы квадратов двухзначных чисел
3. Формула
Древнего Вавилона
4. Канадский метод
5. Способ разложения на простые множители
6. Метод вычетов нечётного числа
7. Метод подбора угадыванием (метод оценки)
8. Метод отбрасывания полного квадрата
9. Извлечение квадратного корня уголком
10. Практическая часть. Диаграммы анкетирования среди 8-11 классах
4. Канадский метод
5. Способ разложения на простые множители
6. Метод вычетов нечётного числа
7. Метод подбора угадыванием (метод оценки)
8. Метод отбрасывания полного квадрата
9. Извлечение квадратного корня уголком
10. Практическая часть. Диаграммы анкетирования среди 8-11 классах
Слайд 5История квадратного корня
Арифметическим квадратным корнем из числа a
называется неотрицательное число, квадрат которого равен данному числу a.
Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически. При переводе греческое слово «сторона» превратилась в «мула» (основание, корень). Поэтому при переводе с индийского на арабский использовался термин «джизр» (корень растения).
Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы алгебраистов в 1525 году. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт и эта черта вскоре слилась со знаком корня.
Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически. При переводе греческое слово «сторона» превратилась в «мула» (основание, корень). Поэтому при переводе с индийского на арабский использовался термин «джизр» (корень растения).
Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы алгебраистов в 1525 году. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт и эта черта вскоре слилась со знаком корня.
Слайд 6Теорема о последней цифре квадрата числа
Если числа оканчиваются цифрами от
1 до 9 и когда мы возводим их в квадрат, то на конце полученного числа будут стоять цифры:
…12=…1 …62=…6
…22=…4 …72=…9
…32=…9 …82=…4
…42=…6 …92=…1
…52=…5
Если в конце числа стоят цифры 2,3,7,8, то полный квадратный корень извлечь из него нельзя.
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки умножаем на это же число плюс единица. К полученному числу справа приписываем 25.
152 = (1∙(1+1))25 = 225
252 = (2∙(2+1))25 = 625
852 = (8∙(8+1))25 = 7225
…12=…1 …62=…6
…22=…4 …72=…9
…32=…9 …82=…4
…42=…6 …92=…1
…52=…5
Если в конце числа стоят цифры 2,3,7,8, то полный квадратный корень извлечь из него нельзя.
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки умножаем на это же число плюс единица. К полученному числу справа приписываем 25.
152 = (1∙(1+1))25 = 225
252 = (2∙(2+1))25 = 625
852 = (8∙(8+1))25 = 7225
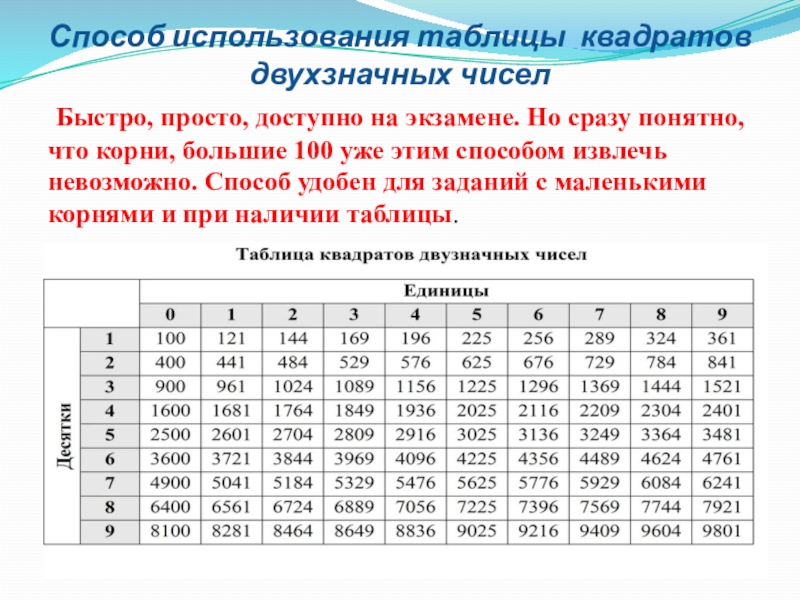
Слайд 7Способ использования таблицы квадратов двухзначных чисел
Быстро, просто, доступно на экзамене.
Но сразу понятно, что корни, большие 100 уже этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
Слайд 8Формула Древнего Вавилона
(Вавилонский метод)
Алгоритм извлечения квадратного корня древневавилонским способом.
Число х представлено в виде суммы а²+ b, где а² ближайший к числу х точный квадрат натурального числа а (а² < х);
Извлечем с помощью этой формулы квадратный корень, например из числа 40:
Этот способ удобен для нахождения
приближённого значения квадратного корня.
Все что нужно - знание формулы.
Извлечем с помощью этой формулы квадратный корень, например из числа 40:
Этот способ удобен для нахождения
приближённого значения квадратного корня.
Все что нужно - знание формулы.
Слайд 9
Канадский метод
Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх знаков после запятой. Вот их формула:
√ X = √ S + (X - S) / (2 √ S)
где X - число, из которого необходимо извлечь квадратный корень, а S - число ближайшего точного квадрата.
Давайте попробуем извлечь квадратный корень из 40
√ 40 = √ 36 + ( 40-36) /(2√ 36)=6+4/12=6+1/3 ≈6,3
Нужно обладать хорошими
вычислительными навыками,
а также знанием формулы.
,
Слайд 10Способ разложения на простые множители
Для извлечения квадратного корня можно разложить
число на простые
множители и извлечь квадратный корень из произведения.
7056│2
3528│2
1764│2
882│2
441│3
147│3
49│7
7│7
√7056 = √ 2²∙2²∙3²∙7² = 2∙2∙3∙7 = 84.
Не всегда легко можно разложить,
чаще до конца не извлекается,
занимает много времени.
множители и извлечь квадратный корень из произведения.
7056│2
3528│2
1764│2
882│2
441│3
147│3
49│7
7│7
√7056 = √ 2²∙2²∙3²∙7² = 2∙2∙3∙7 = 84.
Не всегда легко можно разложить,
чаще до конца не извлекается,
занимает много времени.
Слайд 11Метод вычетов нечётного числа (арифметический способ)
Суть метода: из подкоренного выражения нужно
последовательно вычитать нечетные числа пока разность не станет равной 0 и посчитать количество вычитаний.
√256=16
256-1, 255-3, 252-5, 247-7, 240-9, 231-11, 220-13, 207-15,
192-17, 175-19, 156-21, 135-23, 112-25, 87-27, 60-29, 31-31=0
Общее количество вычитаний равно 16.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее.
256-1, 255-3, 252-5, 247-7, 240-9, 231-11, 220-13, 207-15,
192-17, 175-19, 156-21, 135-23, 112-25, 87-27, 60-29, 31-31=0
Общее количество вычитаний равно 16.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее.
Слайд 12Метод подбора угадыванием (метод оценки)
Рассмотрим пример извлечения квадратного корня из числа
7056.
6400 < 7056 < 8100 802 < 7056 < 902 80 < √7056 < 90.
Квадратный корень из 7056 обязательно заканчивается на 4 или на 6 Получаем:
80< √7056 <90;
√7056 = …4 или √7056 = …6
Корень лежит в пределах от 80 до 90, значит, это числа 84 и 86.
Далее возводим 85 в квадрат, так как это «золотая середина»:
85 2 = (8∙(8+1))25 = 7225, 7225 > 7056;
Получилось, что √7056 = 84.
Данный метод эффективно применяется при вычислении квадратных корней из чисел в диапазоне от 100 до 10 000.
6400 < 7056 < 8100 802 < 7056 < 902 80 < √7056 < 90.
Квадратный корень из 7056 обязательно заканчивается на 4 или на 6 Получаем:
80< √7056 <90;
√7056 = …4 или √7056 = …6
Корень лежит в пределах от 80 до 90, значит, это числа 84 и 86.
Далее возводим 85 в квадрат, так как это «золотая середина»:
85 2 = (8∙(8+1))25 = 7225, 7225 > 7056;
Получилось, что √7056 = 84.
Данный метод эффективно применяется при вычислении квадратных корней из чисел в диапазоне от 100 до 10 000.
Слайд 13Метод отбрасывания полного квадрата
Таким образом можно извлекать только квадратные корни
до числа 75² =5625!
√(2209)= √(2200+9)= √(2200+3²)= 22+25 =47
Извлечение корней после 75²= 5625, вычисляются следующим образом:√7056= √(6800+256)= √6800+16² = 68+16 =84.
Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм зависит от величины подкоренного числа.
√(2209)= √(2200+9)= √(2200+3²)= 22+25 =47
Извлечение корней после 75²= 5625, вычисляются следующим образом:√7056= √(6800+256)= √6800+16² = 68+16 =84.
Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм зависит от величины подкоренного числа.
Слайд 15Практическая часть. Диаграммы анкетирования среди учащихся 8-11 классах
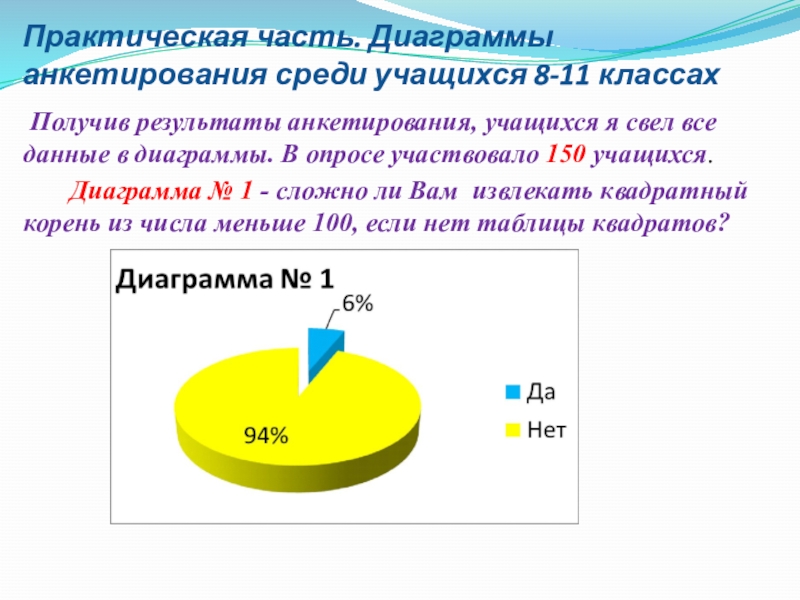
Получив результаты анкетирования,
учащихся я свел все данные в диаграммы. В опросе участвовало 150 учащихся.
Диаграмма № 1 - сложно ли Вам извлекать квадратный корень из числа меньше 100, если нет таблицы квадратов?
Диаграмма № 1 - сложно ли Вам извлекать квадратный корень из числа меньше 100, если нет таблицы квадратов?
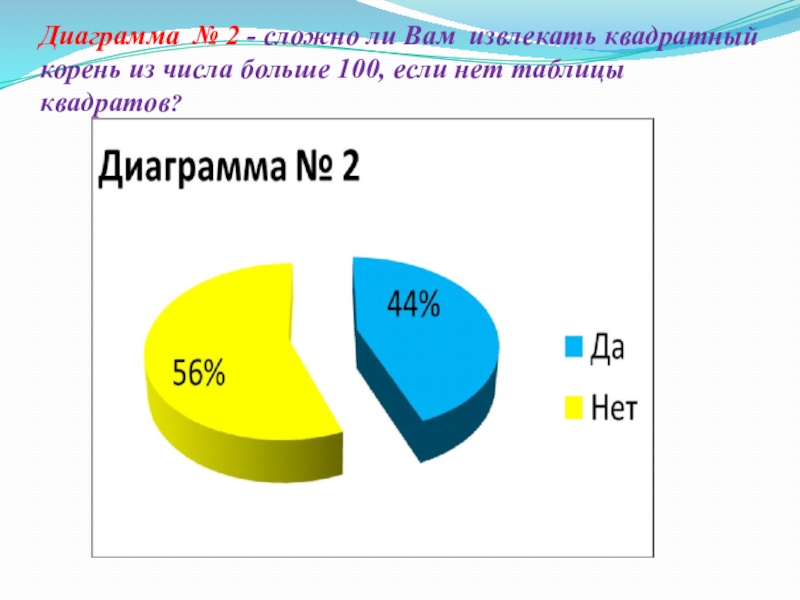
Слайд 16Диаграмма № 2 - сложно ли Вам извлекать квадратный корень из
числа больше 100, если нет таблицы квадратов?
Слайд 19Заключение
В ходе исследования было выявлено, что современной науке
известно много способов извлечения квадратного корня, начиная со способа математиков Древнего Вавилона и заканчивая способом степенных рядов сложных степеней из разделов высшей математики. Были изучены и отработаны на практике все найденные способы. Наше предположение, что существует не менее двух-трех способов извлечения квадратных корней без калькулятора подтвердилось.
Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать при проверке своего решения и не зависеть от наличия в кармане калькулятора. Тем более на экзамене в 9 и 11 классах применение калькулятора не допускается.
Таким образом, цель работы достигнута, задачи выполнены.
Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать при проверке своего решения и не зависеть от наличия в кармане калькулятора. Тем более на экзамене в 9 и 11 классах применение калькулятора не допускается.
Таким образом, цель работы достигнута, задачи выполнены.