- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Исследование функций (10 класс)
Содержание
- 1. Презентация по алгебре на тему Исследование функций (10 класс)
- 2. «НАЧИНАТЬ ИССЛЕДОВАНИЯ МОЖНО ПО-РАЗНОМУ... Все равно начало
- 3. Что называется числовой функцией?Числовой функцией с областью
- 4. 3. Какие из линий, изображённых на рисунке являются графиками функций?
- 5. Слайд 5
- 6. Ответы к тесту:Вариант 1
- 7. Схема
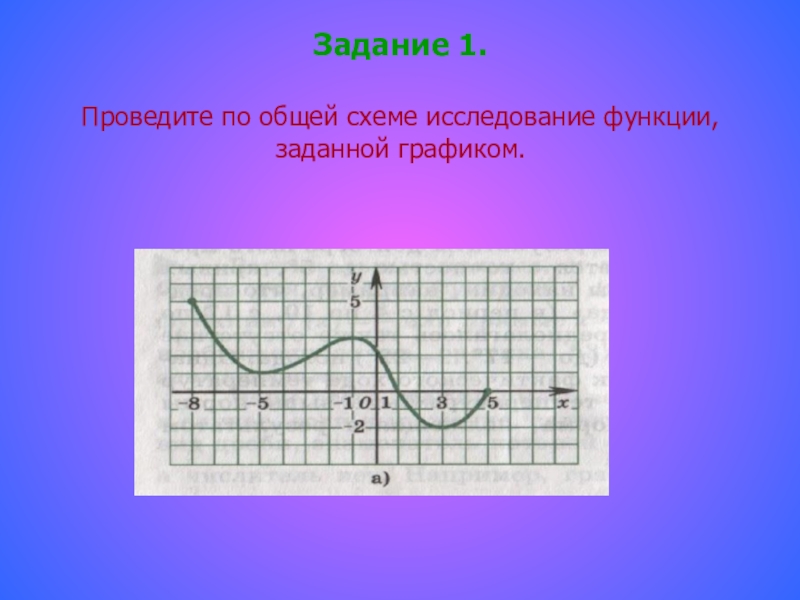
- 8. Задание 1.Проведите по общей схеме исследование функции, заданной графиком.
- 9. 1. Область определения функции D(у) =[-8; 5].
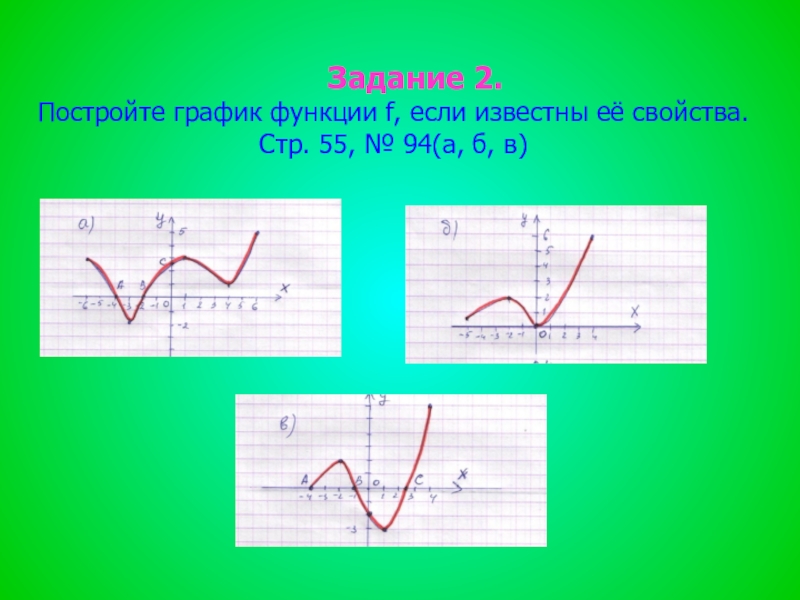
- 10. Задание 2. Постройте
- 11. Защита проектов по теме: «Построение функций по общей схеме исследования»
- 12. Задание группы 1. Построить график функции
- 13. Исследование функции
- 14. Построим график функции f(х) = 2х –
- 15. Слайд 15
- 16. Выдвигаем гипотезу:Графиком функции у =
- 17. Исследуем функцию у = х3 – 1
- 18. 5. х2 = 1, х1 = 0.
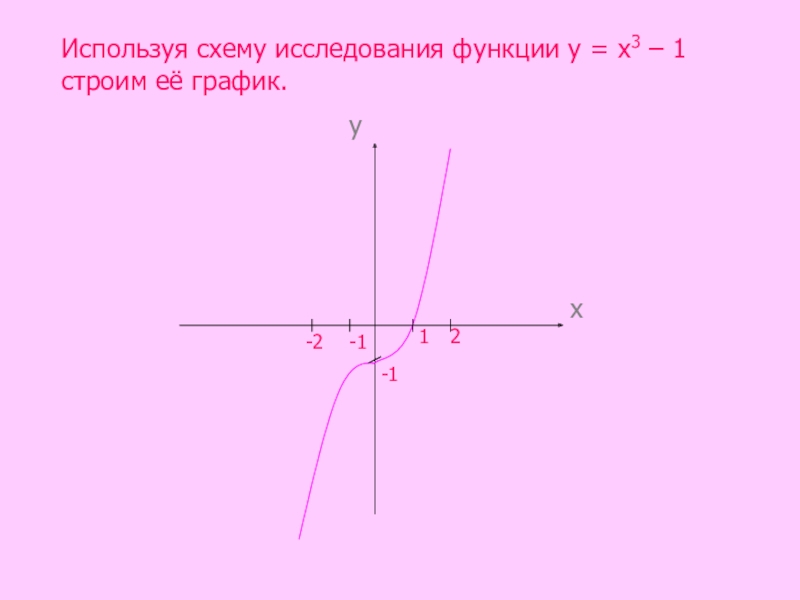
- 19. Используя схему исследования функции у = х3 – 1 строим её график.ху1-12-1-2
- 20. Сделаем вывод.Графиком функции у
- 21. Задание группы 3. Построить
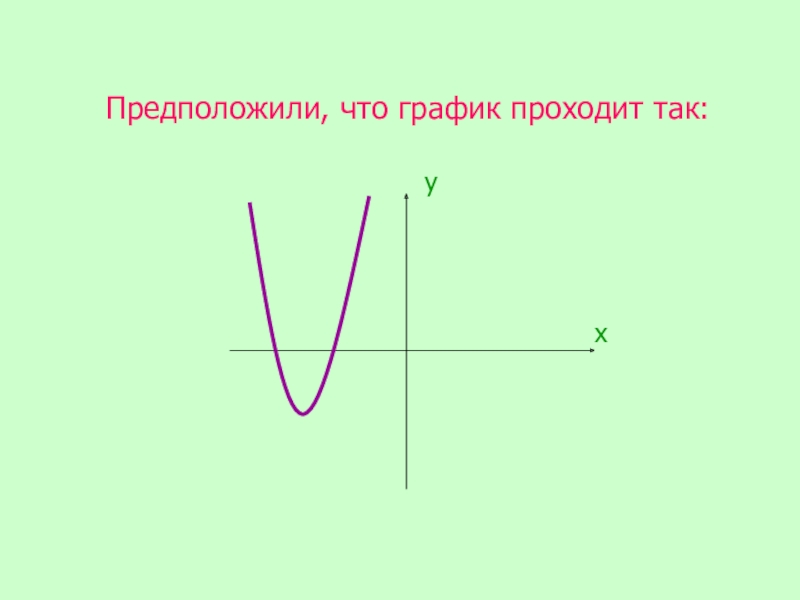
- 22. Графиком функции у = х2 – 4х является парабола. Гипотеза
- 23. Предположили, что график проходит так:ху
- 24. Исследуем функцию у =
- 25. 4. Промежутки знакопостоянства: f(х) >
- 26. 5. Промежутки возрастания и убывания функции:
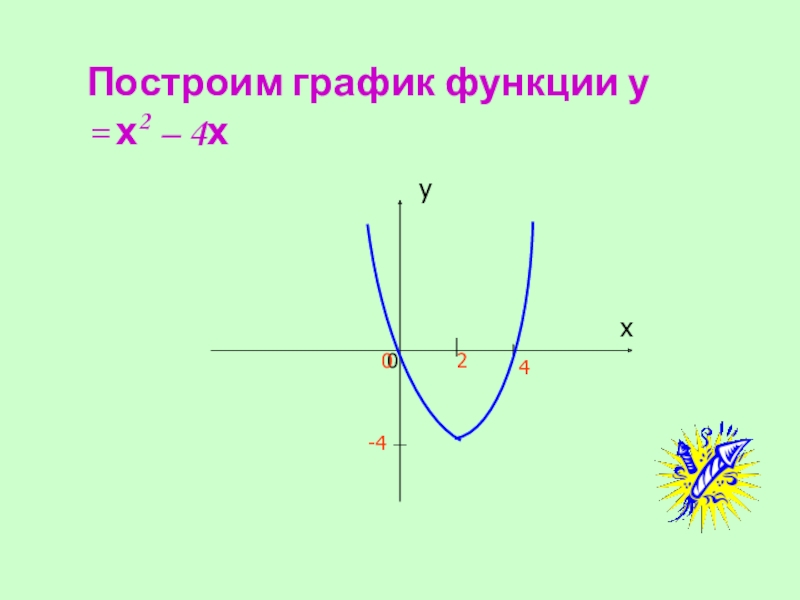
- 27. Построим график функции у = х2 – 4х 200-44ху
- 28. ВыводГрафиком функции у = х2 – 4х является парабола, ветви параболы направлены вверх.
- 29. Задание группы 4. Построить график функции
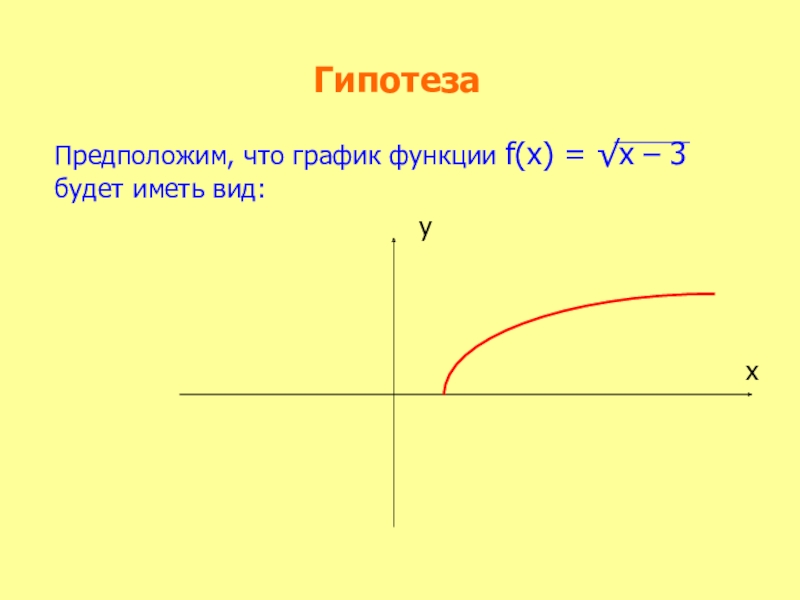
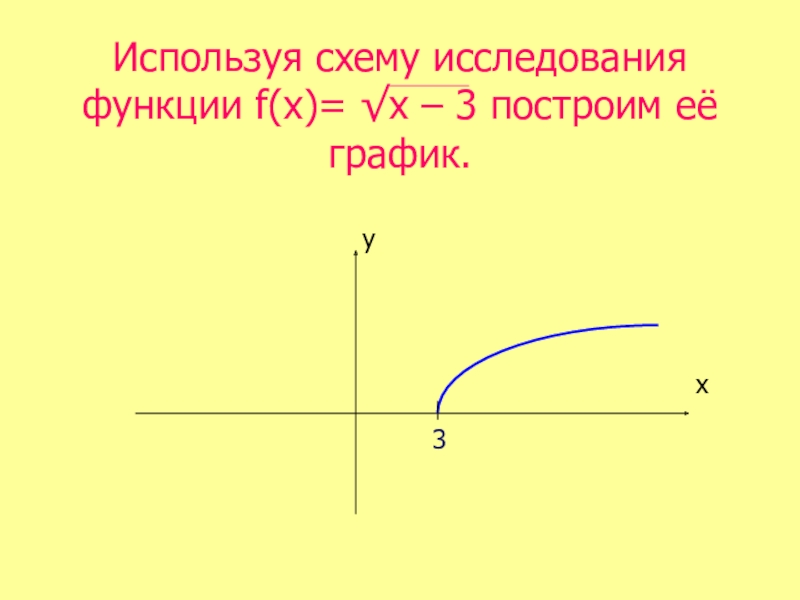
- 30. ГипотезаПредположим, что график функции f(х) = √х – 3 будет иметь вид:ху
- 31. Исследуем функцию f(х) = √х – 3
- 32. Промежутки возрастания и убывания функции:
- 33. Используя схему исследованияфункции f(х)= √х – 3 построим её график.ху3
- 34. Вывод:Гипотеза подтвердилась. Мы построили график функции f(х)= √х – 3.
- 35. Работа по таблице Среди данных графиков
- 36. Задание по карточкам сборника ЕГЭ
- 37. Рефлексия
- 38. Слайд 38
Слайд 2«НАЧИНАТЬ ИССЛЕДОВАНИЯ МОЖНО ПО-РАЗНОМУ... Все равно начало почти всегда оказывается весьма
ЭПИГРАФ К УРОКУ:
Дени Дидро
Слайд 3Что называется числовой функцией?
Числовой функцией с областью определения D называется соответствие,
2. Что называется графиком функции?
Графиком функции f называется множество всех точек (х;у) координатной плоскости, где у=f(х), а х «пробегает» всю область определения функции f.
Вопросы:
Слайд 5
Вопросы:
Графиком функции у = х2 является …
Вертикальную координатную прямую на
координатной плоскости называют осью…
3. Графиком функции у = 1/х является …
4. Зависимость, при которой каждому значению х ставится в соответствие единственное значение у называется …
5. Множество всех точек (х;у) координатной плоскости, где у = f(х), а х «пробегает» всю область определения функции f.
6. Графиком функции у = кх + в является …
7. Горизонтальную координатную прямую на координатной плоскости называют осью…
8. Ось х и ось у называют осями …
г
р
а
а
а
а
а
а
п
п
ф
ф
р
б
о
л
и
к
р
р
б
л
о
г
о
о
к
и
и
с
с
с
п
е
я
м
я
д
и
н
б
ц
к
р
д
и
н
т
у
ц
я
т
1
2
3
4
6
5
7
8
Кроссворд
Слайд 6 Ответы к тесту:
Вариант 1
Б
Б
Б
В
Вариант 2
А
Б
А
В
Б
Оценки:
нет ошибок «5»
1 ошибка «4»
2 ошибки «3»
3 и более «2»
Вариант 3
Б
Б
А
Б
В
Слайд 7 Схема исследования функций:
1. Найти область
2. Определить чётность или нечётность функции, периодичность.
3. Найти координаты точек пересечения графика с осями координат.
1. Найти промежутки знакопостоянства функции.
5. Определить промежутки возрастания или убывания функции.
6. Найти точки экстремума функции, вид экстремума (максимум или минимум) и значения функции в этих точках.
7. Найти область значений функции.
8. Построить график функции.
Слайд 91. Область определения функции D(у) =[-8; 5].
2.
3. Пересечение с осью ОХ: (1; 0), (5; 0).
с осью ОУ: (0; 2).
1. Промежутки знакопостоянства:
f(х) > 0, при х принадлежащем промежутку [-8; 1).
f(х) < 0, при х принадлежащем промежутку (1; 5].
5. Функция возрастает на промежутке [-5; -1]U[3; 5].
Функция убывает на промежутке [-8; -5]U[-1; 3].
6. Точки экстремума: хmax=-1, уmax= 3, хmin= -5, уmin= 1,
хmin= 3, уmin= -2.
7. Область значений Е(у) = [-2; 5].
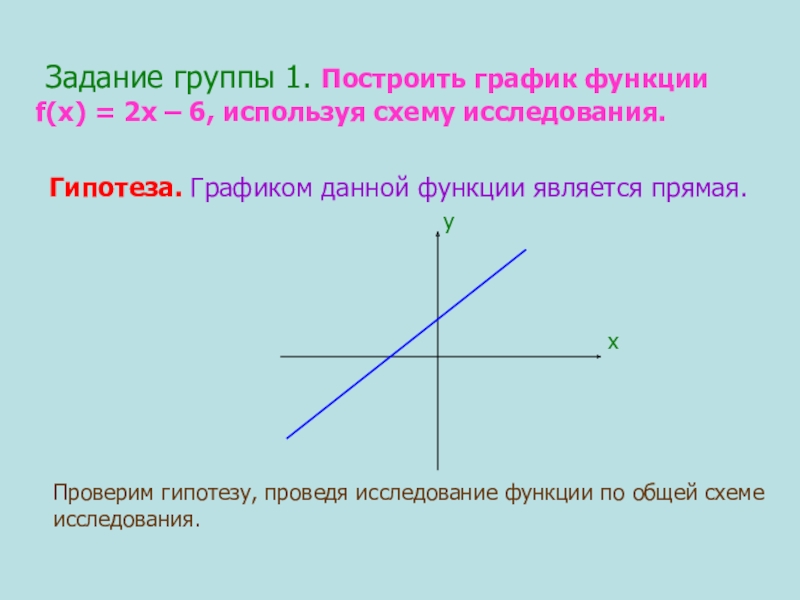
Слайд 12 Задание группы 1. Построить график функции
f(х) = 2х –
Гипотеза. Графиком данной функции является прямая.
х
у
Проверим гипотезу, проведя исследование функции по общей схеме
исследования.
Слайд 13 Исследование функции f(х) = 2х –
Область определения функции D(у) =(-∞; +∞).
2. f(- х) = 2(-х) – 6 = – 2х – 6 = -(2х + 6) – функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
2х – 6 = 0, 2· 0 – 6 = у,
2х = 6, 0 – 6 = у,
х = 3 у = - 6.
(3; 0). (0; -6).
4. Промежутки знакопостоянства:
f(х) > 0, 2х - 6 > 0, 2х > 6, х > 3. (3; +∞).
f(х) < 0, 2х – 6 < 0, 2х < 6, х < 3. (-∞; 3).
5. Функция возрастает на промежутке (-∞; +∞), т. к. к =2, к> 0.
6. Точек экстремума нет.
7. Область значений Е(у) = (-∞; +∞).
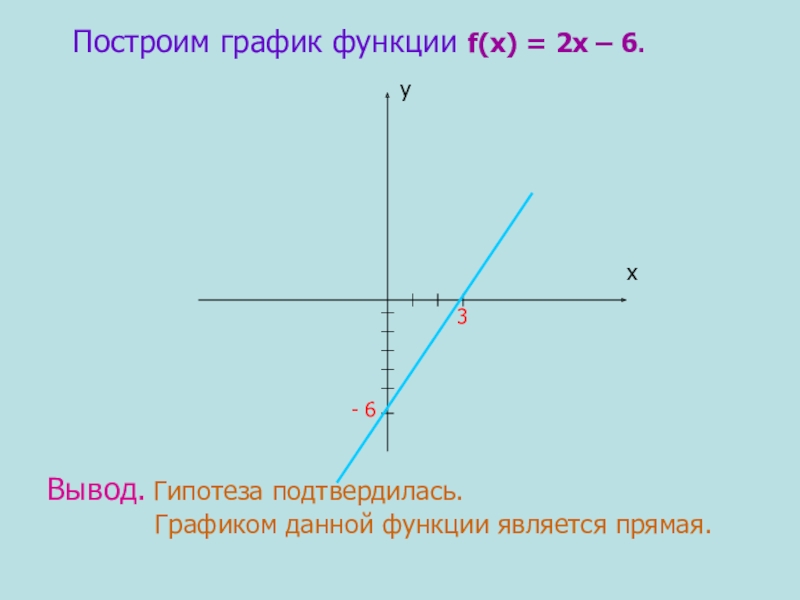
Слайд 14Построим график функции f(х) = 2х – 6.
3
- 6
х
у
Вывод. Гипотеза подтвердилась.
Графиком данной функции является прямая.
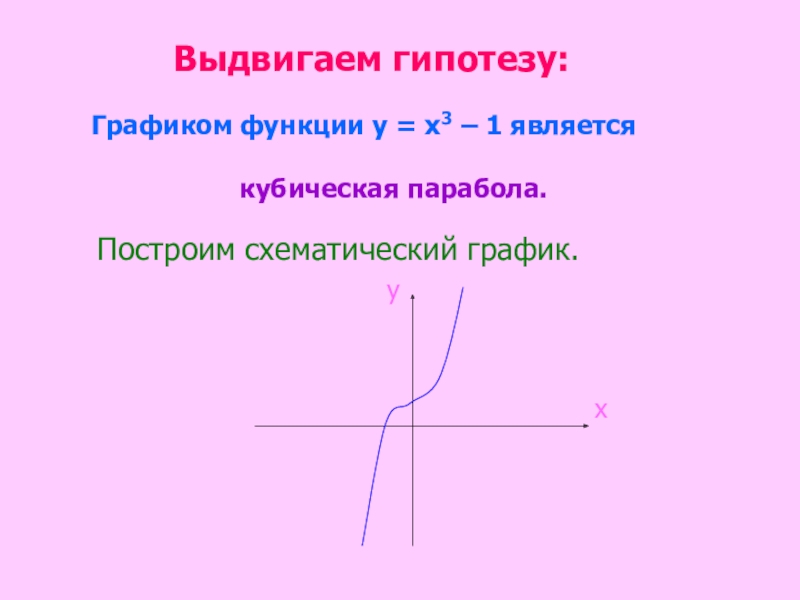
Слайд 16 Выдвигаем гипотезу:
Графиком функции у = х3 – 1 является
кубическая парабола.
Построим схематический график.
х
у
Слайд 17Исследуем функцию у = х3 – 1
1. Область определения функции
2. f(- х) = (-х)3 – 1 = – х3 – 1 = -(х3 + 1) – функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
х3 – 1 = 0, у = 03 – 1,
х3 = 1, у = - 1.
х = 1. (0; -1).
(1; 0).
4. Промежутки знакопостоянства:
f(х) > 0, х3 - 1 > 0, х3 > 1, х > 1. (1; +∞).
f(х) < 0, х3 – 1 < 0, х3 < 1, х < 1. (-∞; 1).
Слайд 185. х2 = 1, х1 = 0.
f(х2) = f(1)
f(х1) = f(0) = 03 – 1 = -1.
х2 > х1, f(х2) > f(х1) – функция возрастает.
6. Точек экстремума нет, т. к. функция возрастает на всей области определения.
7. Область значений Е(у) = (-∞; +∞).
Слайд 20 Сделаем вывод.
Графиком функции у = х3 – 1
опущенная на 1 единицу вниз.
Слайд 24 Исследуем функцию у = х2 – 4х
1.
2. f(- х) = (-х)2 – 4(-х) = х2 + 4х = -(-х2 – 4х) – функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
х2 – 4х = 0, у = 02 - 4 · 0 = 0,
х(х – 4) = 0, у = 0.
х = 0 или х- 4 = 0 (0; 0)
х = 4.
(0; 0). (4; 0).
Найдём вершину параболы: х = 4 : 2 = 2;
у = 22 - 4· 2 = 4 – 8 = - 4.
(2; -4) – вершина параболы.
Слайд 254. Промежутки знакопостоянства:
f(х) > 0, х2 –
Х2 – 4х = 0, х(х -4) = 0,
х = 0 или х- 4 = 0.
х = 4.
f(х) > 0, ( -∞; 0)U(4; +∞).
f(х) < 0, (0; 4).
0
4
−
+
+
х
Слайд 265. Промежутки возрастания и убывания функции:
х2 = 1, х1
f(х2) = f(1) = 12 – 4·1 = -3.
f(х1) = f(0) = 02 – 4·0 = 0.
х2 > х1, f(х2) < f(х1) – функция убывает на промежутке (- ∞;2).
х1 = 3, х2 = 4.
f(х1) = f(3) = 32 – 4·3 = -3.
f(х2) = f(4) = 42 – 4·4 = 0.
х2 > х1, f(х2) > f(х1) – функция возрастает на промежутке (2; +∞).
6. Точка минимума (2; -4).
7. Область значений Е(у) = (-4; +∞).
Слайд 31Исследуем функцию f(х) = √х – 3 по схеме исследования.
1. Область
2. f(- х) = √(-х) - 3 = √- х - 3 – функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
√х - 3 = 0, у = √0 – 3 = √– 3.
х - 3 = 0, точек пересечения нет.
х = 3.
(3; 0).
4. Промежутки знакопостоянства:
f(х) > 0, √х - 3 > 0, х – 3 > 0, х > 3. (3; +∞).
Слайд 32Промежутки возрастания и убывания функции:
х2 = 4, х1
f(х2) = f(4) = √4 – 3 = √1 = 1, 1> 0.
f(х1) = f(3) = √3 – 3 = 0.
х2 > х1, f(х2) > f(х1) – функция возрастает.
6. Точек экстремума нет, т к функция возрастает.
7. Область значений Е(у) = (0; +∞).
Слайд 35 Работа по таблице
Среди данных графиков найти тот, который
Слайд 38
Домашнее задание
На
f(х) = х + 5
На оценку «4» исследовать функцию
f(х) = х2 – 5х + 6.
На оценку «5» исследовать функцию
f(х) = √(х–2) - 2.







![Презентация по алгебре на тему Исследование функций (10 класс) 1. Область определения функции D(у) =[-8; 5]. 2. Функция ни 1. Область определения функции D(у) =[-8; 5]. 2. Функция ни чётная, ни нечетная. Функция](/img/thumbs/d22f488b7455333119deccb66eadbdf9-800x.jpg)