Презентация, доклад по алгебре на тему функции обратные к тригонометрическим

Содержание

1. Презентация по алгебре на тему функции обратные к тригонометрическим
2. ЦЕЛИ УРОКАНаучиться решать уравнения вида cos x
3. Устные упражненияНайти значения: sin
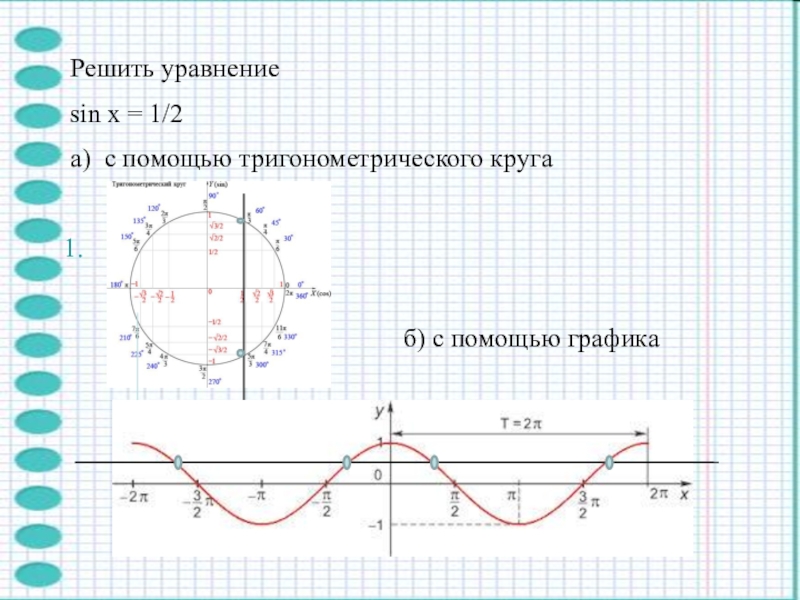
4. Решить уравнениеsin x = 1/2а) с помощью
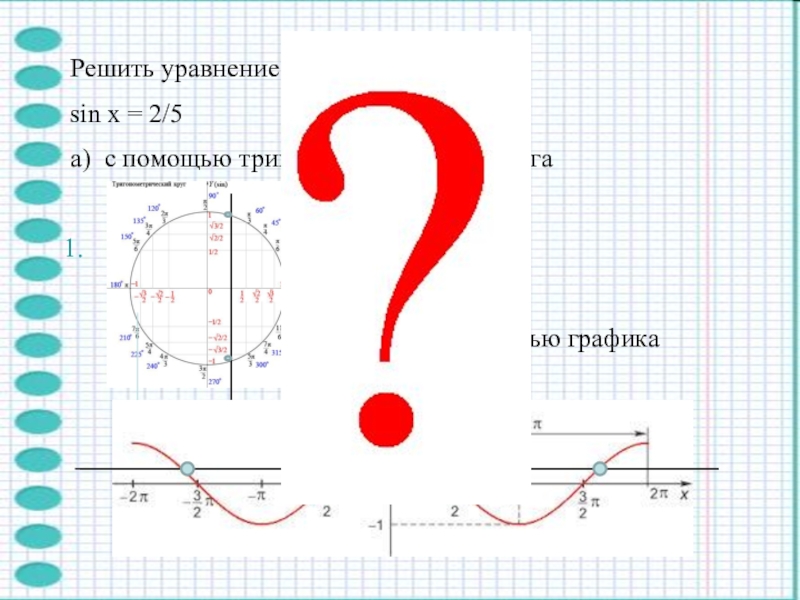
5. Решить уравнениеsin x = 2/5 а) с
6. Arccos х Арккосинусом числа m называется такой
7. 1)Область определения: отрезок [-1; 1]; 2) Область
8. Arcsin
9. Свойства функции y = arcsin x 1)Область
10. ArctgхАрктангенсом
11. y=arctg
12. arcctg
13. Функция y=arcctg x непрерывна и ограничена на
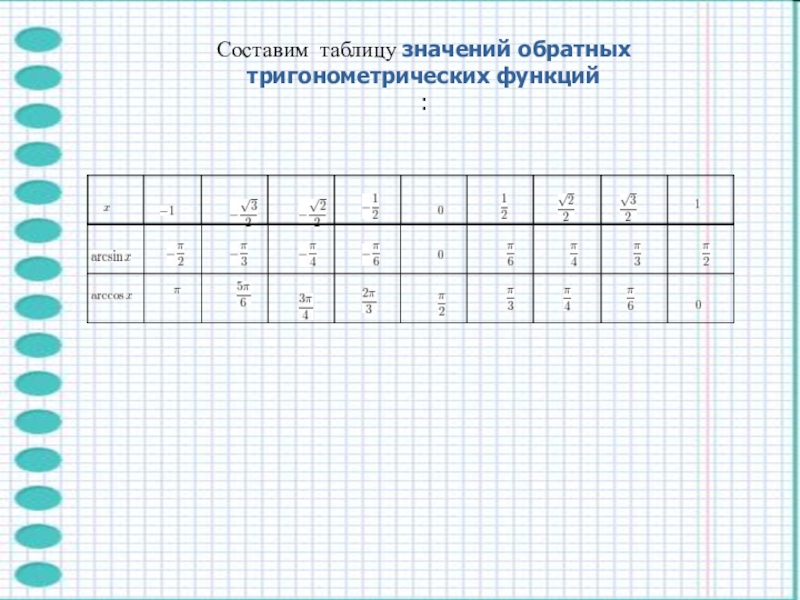
14. Составим таблицу значений обратных тригонометрических функций:
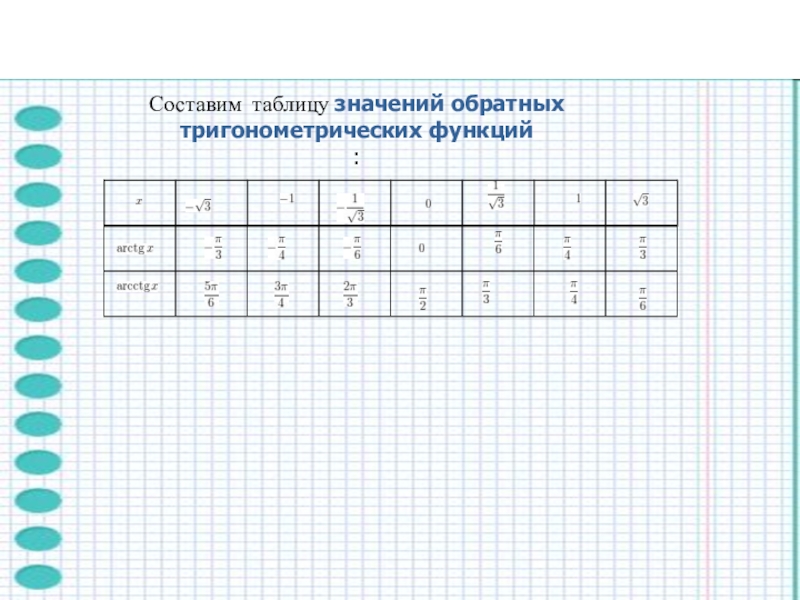
15. Составим таблицу значений обратных тригонометрических функций:
16. Основные соотношения для обратных тригонометрических функций:sin(arcsinx)=x,

ЦЕЛИ УРОКАНаучиться решать уравнения вида cos x = a, sin x = a, tg x = a, ctg x = aПознакомиться с функциями y = arccos x,

Главная
Алгебра
Презентация по алгебре на тему функции обратные к тригонометрическим

Слайд 1РЕШЕНИЕ тригонометрических уравнений.
Обратные тригонометрические функции.

Слайд 2ЦЕЛИ УРОКА

Научиться решать уравнения вида cos x = a,

sin x = a, tg x = a, ctg x = a
Познакомиться с функциями y = arccos x, y = arcsin x , y = arctg x, y = arcctg x. Их графиками и свойствами.
3. Узнать основные соотношения для обратных тригонометрических функций:

ЦЕЛИ УРОКАНаучиться решать уравнения вида cos x = a, sin x = a,

Слайд 3Устные упражнения
Найти значения:
sin 45°=

sin 135°=
cos π/3 = sin π/3 =
cos π/6 = sin π/6 =
tg π/3 = tg π/6 =
sin 2π/3 = сos 2π/3 = -
sin π/4 = сos 5π/4 = -

Слайд 4Решить уравнение
sin x = 1/2
а) с помощью тригонометрического круга

б) с помощью графика

Слайд 5Решить уравнение
sin x = 2/5
а) с помощью тригонометрического круга

б) с помощью графика

Слайд 6Arccos х

Арккосинусом числа m называется такой угол x, для которого

сos x=m,
0 ≤ X ≤ π, |m|≤1
Функция y = cos x непрерывна и ограничена на всей своей числовой прямой.
Функция y = arccos x является строго убывающей.
График обратной функции y = arccos x симметричен с графиком основной функции сos x=m относительно биссектрисы I - III координатных углов.

Arccos х Арккосинусом числа m называется такой угол x, для которого сos x=m, 0 ≤

Слайд 71)Область определения: отрезок [-1; 1];
2) Область значений: отрезок [

0, π ];

3) Функция y = arccos x ни четная ни нечётная: arcсоs (-x) = π - arcсоs x;

4) Функция y = arccos x
монотонно убывающая;

5)График пересекает оси Ох, Оу
в начале координат.

Свойства функции y = arccos x .

1)Область определения: отрезок [-1; 1]; 2) Область значений: отрезок [ 0, π ];3) Функция y =

Слайд 8 Arcsin х
Арксинусом числа m называется

такой угол x, для которого sinx=m, -π/2≤X≤π/2,|m|≤1
Функция y = sinx непрерывна и ограничена на всей своей числовой прямой.
Функция y = arcsinx является строго возрастающей.
График обратной функции симметричен с графиком основной функции относительно биссектрисы I - III координатных углов.

Arcsin хАрксинусом числа m называется такой угол x, для которого sinx=m,

Слайд 9Свойства функции y = arcsin x
1)Область определения: отрезок [-1; 1];

2)Область изменения: отрезок [-π/2,π/2];
3)Функция y = arcsin x нечетная: arcsin (-x) = - arcsin x;
4)Функция y = arcsin x монотонно возрастающая;
5)График пересекает оси Ох, Оу в начале координат.

Свойства функции y = arcsin x 1)Область определения: отрезок [-1; 1]; 2)Область изменения: отрезок

Слайд 10 Arctgх
Арктангенсом числа m
называется такой

угол x,
для которого tgx=m,
-π/2График функции y=arctgx
Получается из графика
Функции y=tgx, симметрией
Относительно прямой y=x.

ArctgхАрктангенсом числа m называется такой угол x, для которого tgx=m, -π/2

Слайд 11 y=arctg х
1)Область определения: R
2)Область

значения: отрезок [-π/2,π/2];
3)Функция y = arctg x нечетная: arctg (-x) = - arctg x;
4)Функция y = arctg x монотонно возрастающая;
5)График пересекает оси Ох, Оу в начале координат.