- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Элементы статистики
Содержание
- 1. Презентация по алгебре на тему Элементы статистики
- 2. Цель урока:1.Рассмотреть статистическую обработку информации
- 3. Линейная диаграмма (многоугольник распределения).
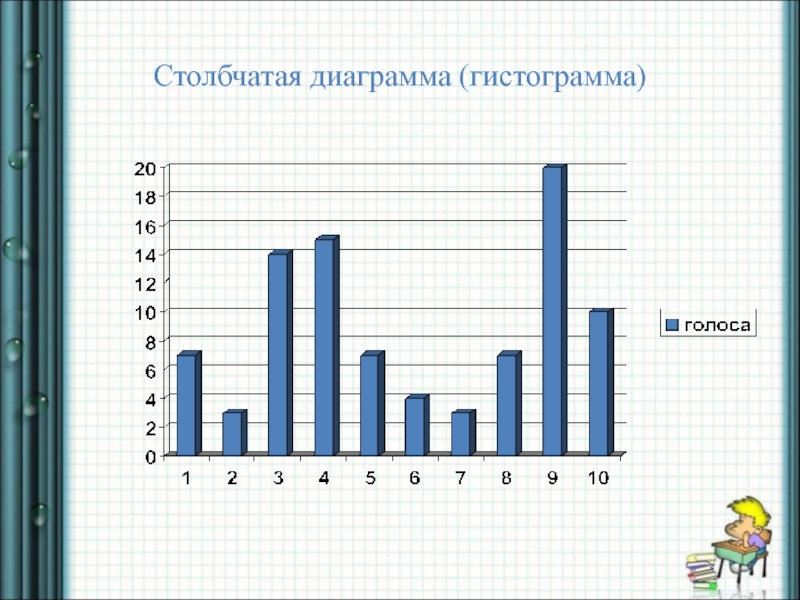
- 4. Столбчатая диаграмма (гистограмма)
- 5. Слайд 5
- 6. статистические методы обработки информации:1. Упорядочивание и группировка
- 7. Статистические характеристики объем измерения размах измерения мода измерения среднее (среднее арифметическое) медиана
- 8. В математике и статистике среднее арифметическое (или
- 9. .Задача: сколько минут тратят на домашнее
- 10. Если расставить выборку по возрастанию (или убыванию)
- 11. Медиана(обозначается Ме)- это так называемое серединное
- 12. Мода.
- 13. В совокупности: 2, 3, 3, 4, 5
- 14. Ряд может иметь две моды, а может
- 15. Разность между наибольшим и наименьшим числом называется
- 16. Пример.26, 23, 18, 25, 20, 25, 30,
- 17. Задача №1.Найти размах,моду и медиану следующей совокупности:-2;
- 18. Если число членов ряда n нечетное ,
- 19. Решение задачи: а)число членов ряда n
- 20. Статистическая информация. Статистическая информация о
- 21. Таблица распределения данных Если среди всех данных
- 22. Объем измерения –это сумма всех кратностей.
- 23. Задачи на закрепление Задача №1.
- 24. Задачи на закрепление.Задача №3. Измерили длины
- 25. «… Ужасен он в окрестной мгле!
- 26. ЛитератураА.Г.Мордкович Алгебра.9кл.:В двух частях. Ч.1:Учеб. для общеобразоват.учреждений.
Цель урока:1.Рассмотреть статистическую обработку информации и ее основные характеристики: объем измерения, мода, размах, среднее2.Ввести понятие варианты, ее кратности и частоты3.Прорешать задачи на закрепление
Слайд 2 Цель урока:
1.Рассмотреть статистическую обработку информации
и ее основные характеристики:
объем
измерения, мода, размах, среднее
2.Ввести понятие варианты, ее кратности и частоты
3.Прорешать задачи на закрепление
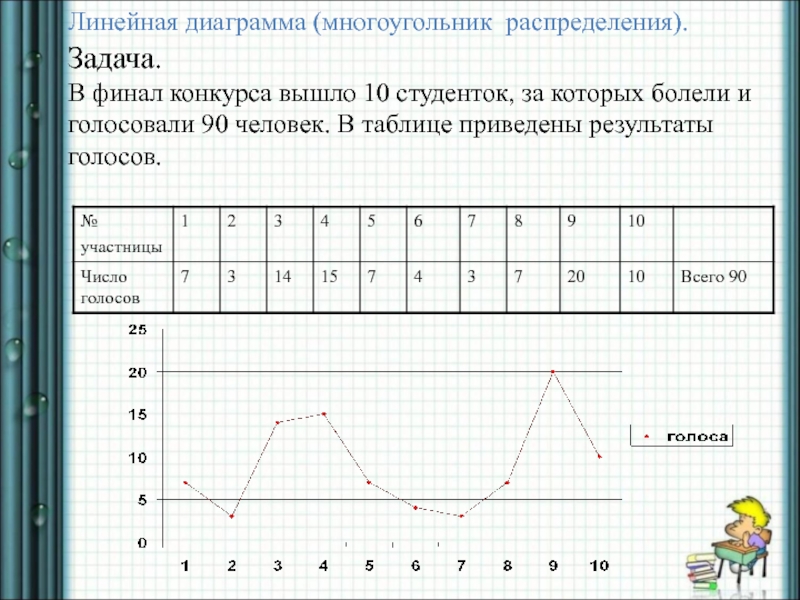
Слайд 3 Линейная диаграмма (многоугольник распределения). Задача. В
финал конкурса вышло 10 студенток, за которых болели и голосовали 90 человек. В таблице приведены результаты голосов.
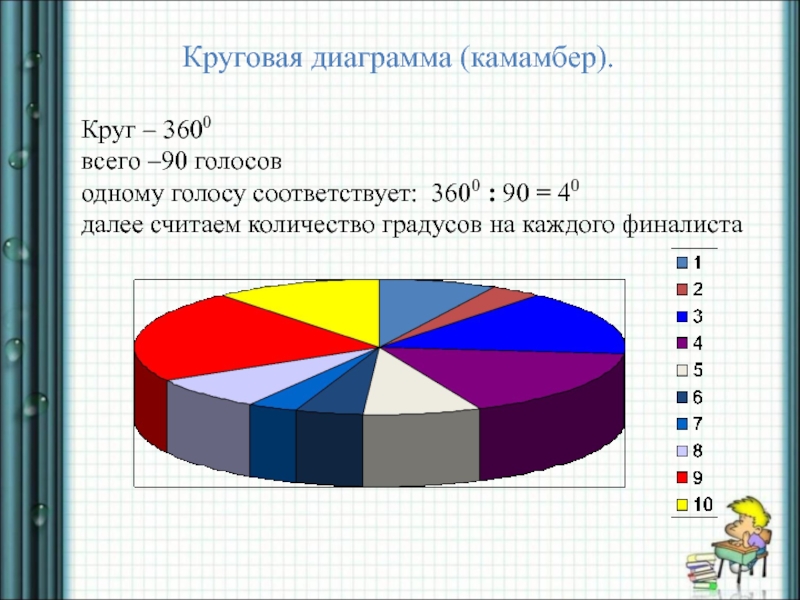
Слайд 5 Круговая диаграмма (камамбер). Круг –
3600
всего –90 голосов
одному голосу соответствует: 3600 : 90 = 40
далее считаем количество градусов на каждого финалиста
Слайд 6статистические методы обработки информации:
1. Упорядочивание и группировка данных.
2. Составление таблицы распределения
данных.
3. Построение графиков распределения данных.
4. Получение паспорта данных, т.е. небольшое количество основных числовых характеристик.
3. Построение графиков распределения данных.
4. Получение паспорта данных, т.е. небольшое количество основных числовых характеристик.
Слайд 7Статистические характеристики
объем измерения
размах измерения
мода измерения
среднее (среднее арифметическое)
медиана
Слайд 8В математике и статистике среднее арифметическое (или просто среднее) набора чисел
— это сумма всех чисел в этом наборе, делённая на их количество.
Для трёх чисел сложим их и поделим на 3:
Для трёх чисел сложим их и поделим на 3:
Слайд 9 .
Задача: сколько минут тратят на домашнее задание по алгебре?
23,
30, 25, 20, 34, 25, 30, 34, 35
23+30+25+20+34+25+30+34+35+14 = 27
10
23+30+25+20+34+25+30+34+35+14 = 27
10
Слайд 10Если расставить выборку по возрастанию (или убыванию) той величины, которой мы
интересуемся, то медиана - это то, что будет ровно посередине "строя".
Например, если мы расположим по порядку длительности интервалы времени:
секунда, минута, час, сутки и неделя –
то медианой будет час.
Например, если мы расположим по порядку длительности интервалы времени:
секунда, минута, час, сутки и неделя –
то медианой будет час.
Слайд 11 Медиана(обозначается Ме)- это так
называемое серединное значение
упорядоченного ряда значений
случайной
величины.
Число членов ряда n=10 – четное число:
3; 3; 3; 4; 4; 5; 5; 5; 8; 12.
Для него медиана равна среднему
арифметическому двух центральных событий: Ме =(4+5)/2=4,5
3 3 3 4 4 5 5 5 8 12
величины.
Число членов ряда n=10 – четное число:
3; 3; 3; 4; 4; 5; 5; 5; 8; 12.
Для него медиана равна среднему
арифметическому двух центральных событий: Ме =(4+5)/2=4,5
3 3 3 4 4 5 5 5 8 12
Слайд 12Мода.
Если мы выстроим
все пары обуви на
складе по цвету, то
самый ходовой цвет
будет модой.
Мода - это то, что непременно должны учитывать производители упаковок и фасовщики.
Если бы большинство людей покупало за один раз стакан молока, молочные пакеты не были бы литровыми. Мода (обозначается Мо) – наиболее часто встречающееся значение случайной величины.
все пары обуви на
складе по цвету, то
самый ходовой цвет
будет модой.
Мода - это то, что непременно должны учитывать производители упаковок и фасовщики.
Если бы большинство людей покупало за один раз стакан молока, молочные пакеты не были бы литровыми. Мода (обозначается Мо) – наиболее часто встречающееся значение случайной величины.
Слайд 13В совокупности: 2, 3, 3, 4, 5 модой является число 3.
Иногда
в совокупности встречается более чем одна мода (например:
2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9).
В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством.
2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9).
В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством.
Слайд 14Ряд может иметь две моды, а может не иметь моды.
Например,
47,46,50,52,47,49,52,55 –
имеет две моды: 47 и 52.
59,68,66,70,67,71,74 – этот ряд не имеет моды.
Слайд 15Разность между наибольшим и наименьшим числом называется размахом ряда чисел.
Обозначается
R.
В совокупности: 2, 3, 3, 4, 5 размахом является число 3 = 5 - 2.
В совокупности: 2, 3, 3, 4, 5 размахом является число 3 = 5 - 2.
Слайд 16Пример.
26, 23, 18, 25, 20, 25, 30, 25, 34, 19.
Выстроим по
возрастанию:
18, 19, 20, 23, 25, 25, 25, 26, 30, 34.
(26+23+18+25+20+25+30+25+34+19): 10= = 245:10 = 24,5
24,5 – среднее арифметическое
34-18 = 16 – размах,
25 – мода,
25 – медиана.
18, 19, 20, 23, 25, 25, 25, 26, 30, 34.
(26+23+18+25+20+25+30+25+34+19): 10= = 245:10 = 24,5
24,5 – среднее арифметическое
34-18 = 16 – размах,
25 – мода,
25 – медиана.
Слайд 17Задача №1.
Найти размах,моду и медиану следующей совокупности:
-2; 3; 4 ; -3;
0; 1; 3; -2; -1; 2; -2; 1.
Задача № 2.
В ряду чисел 3; 8; 15; 30; - ; 24 пропущено одно число. Найдите его, если:
а) среднее арифметическое ряда равно 18;
б) размах ряда равен 40;
в) мода ряда равна 24.
Задача № 3.
Выборка 130; 141; 151; 142; 129; 144; 129; 147; 145; 150 содержит сведения о росте (в сантиметрах) каждого из 10 обследованных школьников. Найдите моду, размах, медиану и среднее.
Задача № 2.
В ряду чисел 3; 8; 15; 30; - ; 24 пропущено одно число. Найдите его, если:
а) среднее арифметическое ряда равно 18;
б) размах ряда равен 40;
в) мода ряда равна 24.
Задача № 3.
Выборка 130; 141; 151; 142; 129; 144; 129; 147; 145; 150 содержит сведения о росте (в сантиметрах) каждого из 10 обследованных школьников. Найдите моду, размах, медиану и среднее.
Слайд 18
Если число членов ряда n нечетное , то
Ме = X [n/2]+1, где [ n/2]-целая часть числа n/2.
Если n четное, то
Ме = (X [n/2]+X [n/2]+1) : 2
Задача.
Найдите медиану ряда чисел:
а) 30; 32; 37; 40; 41; 42; 45; 49; 52;
б) 102; 104; 205; 207; 327; 408; 417;
в) 16; 18; 20; 22; 24; 26;
г) 1,2; 1,4; 2,2; 2,6; 3,2; 3,8; 4,4; 5,6.
Если n четное, то
Ме = (X [n/2]+X [n/2]+1) : 2
Задача.
Найдите медиану ряда чисел:
а) 30; 32; 37; 40; 41; 42; 45; 49; 52;
б) 102; 104; 205; 207; 327; 408; 417;
в) 16; 18; 20; 22; 24; 26;
г) 1,2; 1,4; 2,2; 2,6; 3,2; 3,8; 4,4; 5,6.
Слайд 19 Решение задачи: а)число членов ряда n = 9, ряд упорядочен.
Ме = X[9/2]+1=X5=41.
б)n =7 , ряд упорядочен.
Ме = X3+1=207.
в) n = 6 , ряд упорядочен .
Ме = (X [n/2] + X [n/2]+1) : 2
Ме = (20+22) : 2 = 21.
г)n =8, ряд упорядочен.
Ме = (X4+X5) : 2 =(2,6+3,2) : 2 =2,9.
Ответ:а)41; б)207; в)21; г)2,9.
Слайд 20Статистическая информация.
Статистическая информация о результатах наблюдений может быть
представлена в различных формах. Простейший из них – это запись результатов в порядке их получения. Данная запись называется простым статистическим рядом.
Отдельные значения, составляющие этот ряд, называют вариантами.
Количество вариант в ряду n называют объемом ряда или объемом выборки.
Например, игральный кубик бросали 12 раз. В результате получили:
3; 4; 5; 6; 6; 6; 5; 1; 4; 6; 1; 4 (n = 12)
Вариантами являются х1=3, х2=4, х3=5, х 4=6, х5 =6, и т.д.
Варианты х4, х 5,х 6, х 10 имеют одинаковые значения, но это разные варианты.
Отдельные значения, составляющие этот ряд, называют вариантами.
Количество вариант в ряду n называют объемом ряда или объемом выборки.
Например, игральный кубик бросали 12 раз. В результате получили:
3; 4; 5; 6; 6; 6; 5; 1; 4; 6; 1; 4 (n = 12)
Вариантами являются х1=3, х2=4, х3=5, х 4=6, х5 =6, и т.д.
Варианты х4, х 5,х 6, х 10 имеют одинаковые значения, но это разные варианты.
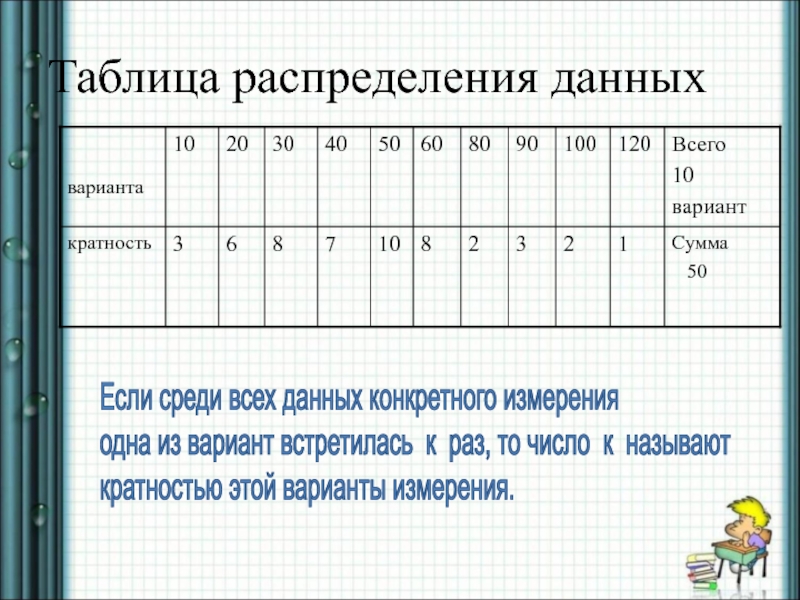
Слайд 21Таблица распределения данных
Если среди всех данных конкретного измерения
одна
из вариант встретилась к раз, то число к называют
кратностью этой варианты измерения.
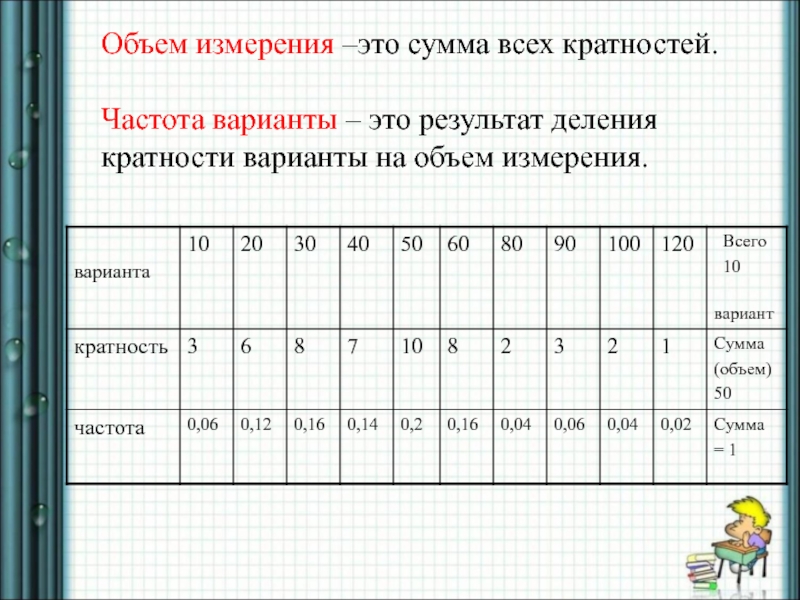
Слайд 22Объем измерения –это сумма всех кратностей. Частота варианты – это результат деления
кратности варианты на объем измерения.
Слайд 23Задачи на закрепление
Задача №1.
Мальчик написал в блокноте
некоторую выборку из 6 чисел, но неаккуратно вырвал листок, и в результате последнее число оказалось утрачено. Сохранились первые числа: -3; 2; 4,5; -2; 2,5. Восстановите утраченное число, если известно, что медиана выборки равна 1.
Задача №2.
Школьник обнаружил, что число оценок, которые он получил по математике за год, равно 20. При этом в дневнике записаны следующие оценки:пятерок – 10, двоек,троек,четверок по 3. Одна оценка не записана. Когда школьник спросил об этой оценке у учителя, тот сказал только, что среднее арифметическое ряда оценок – число целое. Какая оценка не записана у ученика?
Задача №2.
Школьник обнаружил, что число оценок, которые он получил по математике за год, равно 20. При этом в дневнике записаны следующие оценки:пятерок – 10, двоек,троек,четверок по 3. Одна оценка не записана. Когда школьник спросил об этой оценке у учителя, тот сказал только, что среднее арифметическое ряда оценок – число целое. Какая оценка не записана у ученика?
Слайд 24Задачи на закрепление.
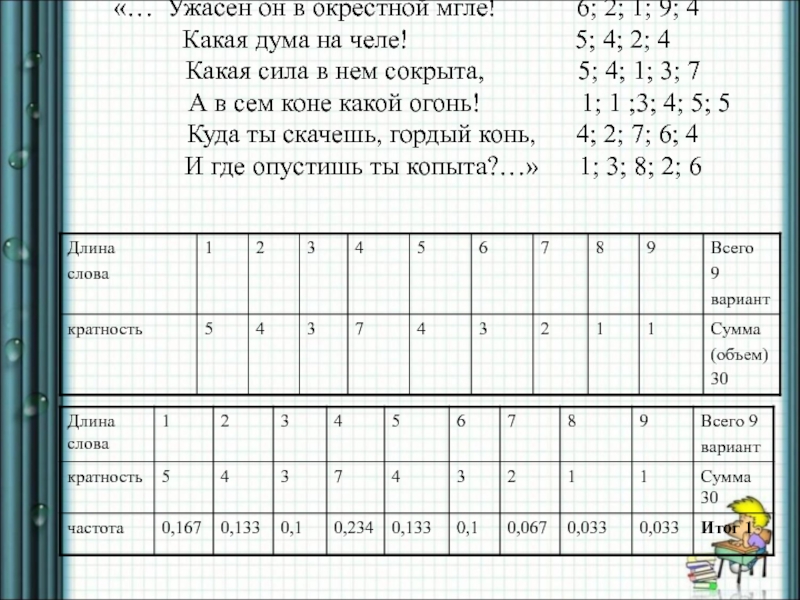
Задача №3.
Измерили длины слов (количество букв) в
приведенном ниже отрывке из поэмы А.С.Пушкина «Медный всадник». Нужно построить таблицы распределения кратностей и частот в зависимости от длины слов.
«…Ужасен он в окрестной мгле!
Какая дума на челе!
Какая сила в нем сокрыта,
А в сем коне какой огонь!
Куда ты скачешь, гордый конь,
И где опустишь ты копыта?…»
«…Ужасен он в окрестной мгле!
Какая дума на челе!
Какая сила в нем сокрыта,
А в сем коне какой огонь!
Куда ты скачешь, гордый конь,
И где опустишь ты копыта?…»
Слайд 25«… Ужасен он в окрестной мгле!
6; 2; 1; 9; 4
Какая дума на челе! 5; 4; 2; 4
Какая сила в нем сокрыта, 5; 4; 1; 3; 7
А в сем коне какой огонь! 1; 1 ;3; 4; 5; 5
Куда ты скачешь, гордый конь, 4; 2; 7; 6; 4
И где опустишь ты копыта?…» 1; 3; 8; 2; 6
Слайд 26Литература
А.Г.Мордкович Алгебра.9кл.:В двух частях. Ч.1:Учеб. для общеобразоват.учреждений. – 8-е изд.испр. –
М.:Мнемозина,2006
А.Г.Мордкович Алгебра.9кл.:В двух частях. Ч.2:задачник для общеобразоват.учреждений.– М.:Мнемозина,2006
Рурукин А.Н.,Масленникова И.А.,Мишина Т.Г. Поурочные разработки по алгебре:9 класс. – М.:ВАКО,2011
Мордкович А.Г. События. Вероятности. Статистическая обработка данных:Доп.параграфы к курсу алгебры 7-9 кл. общеобразоват.учреждений./А.Г. Мордкович, П.В.Семенов. – 4-е изд. – М.:Мнемозина,2006
Решение задач по статистике, комбинаторике и теории вероятностей.7-9 классы. Авт.сост.В.Н.Студенецкая. Изд.2-е,испр. – Волгоград: Учитель,2006
Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы:9 класс.
Шестаков С.А.,Высоцкий И.Р.,Звавич Л.И.;Под редакцией С.А.Шестакова. – М.:ООО «Издательство АСТ»:ООО «Издательство Астрель», 2005
А.Г.Мордкович Алгебра.9кл.:В двух частях. Ч.2:задачник для общеобразоват.учреждений.– М.:Мнемозина,2006
Рурукин А.Н.,Масленникова И.А.,Мишина Т.Г. Поурочные разработки по алгебре:9 класс. – М.:ВАКО,2011
Мордкович А.Г. События. Вероятности. Статистическая обработка данных:Доп.параграфы к курсу алгебры 7-9 кл. общеобразоват.учреждений./А.Г. Мордкович, П.В.Семенов. – 4-е изд. – М.:Мнемозина,2006
Решение задач по статистике, комбинаторике и теории вероятностей.7-9 классы. Авт.сост.В.Н.Студенецкая. Изд.2-е,испр. – Волгоград: Учитель,2006
Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы:9 класс.
Шестаков С.А.,Высоцкий И.Р.,Звавич Л.И.;Под редакцией С.А.Шестакова. – М.:ООО «Издательство АСТ»:ООО «Издательство Астрель», 2005














![Презентация по алгебре на тему Элементы статистики Если число членов ряда n нечетное , то Ме Если число членов ряда n нечетное , то Ме = X [n/2]+1, где [](/img/thumbs/c1dba524bcfd51818ef84a32dc6197d3-800x.jpg)