Презентация, доклад по алгебре на тему Четность и нечетность функций

Содержание

1. Презентация по алгебре на тему Четность и нечетность функций
2. Цель урока: Формирование понятий «
3. 1) Область определения функций .2) Монотонность функции.3)
4. Запомнить:Функцию y=f(x), x∈X, называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x). График
5. Понятие симметричности Если числовое множество Х
6. Определите симметричное множество или нет (-9; 9),
7. y = x²-1y = |x|y = x³
8. Установить , симметрична ли область определения функции2)
9. y = 7x +x³ Решение:y (- x)=
10. 1. f(x) =7 x2+x42.
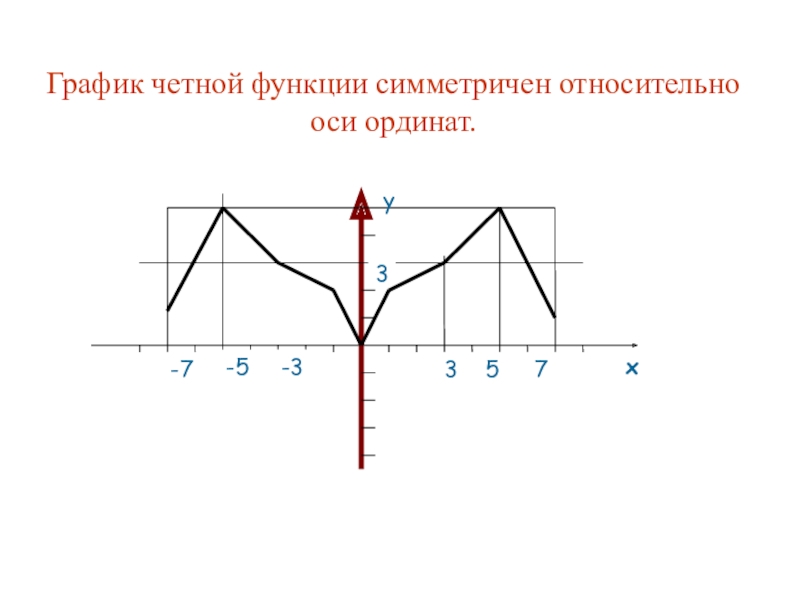
11. График четной функции симметричен относительно оси ординат.
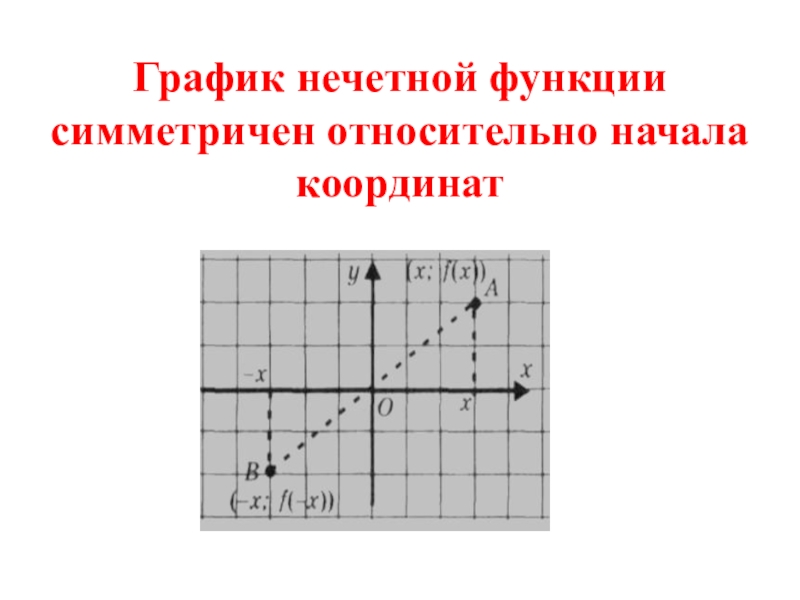
12. График нечетной функции симметричен относительно начала координат
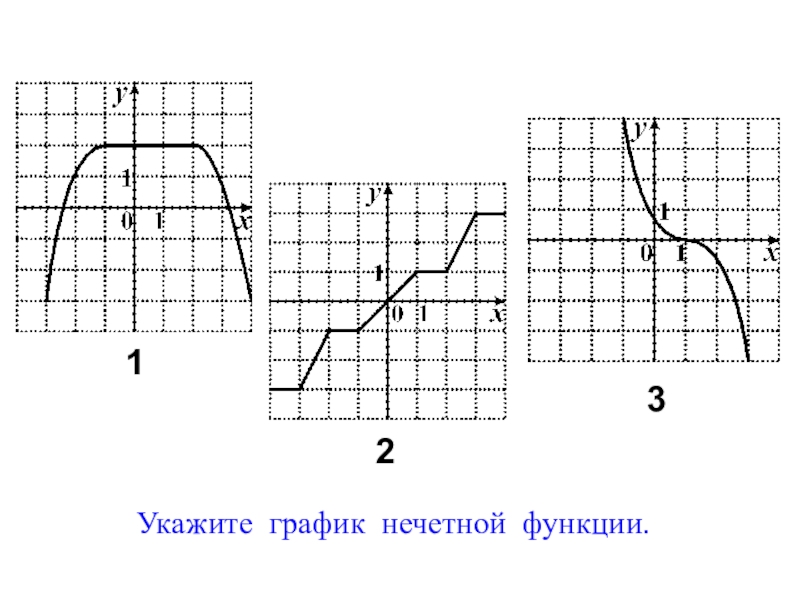
13. Укажите график нечетной функции.123
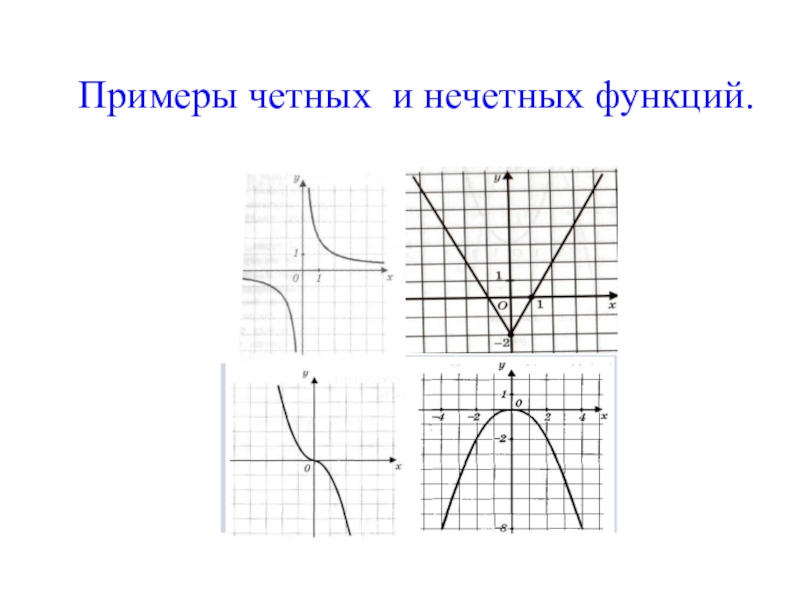
14. Примеры четных и нечетных функций.
15. . Подведение итогов.- Какие функции называются четными?-
16. Спасибо за урок

Цель урока: Формирование понятий « четность нечетность функции»; исследование функций на четность; определение по графику четных и нечетных функций; построение графиков функций, содержащих модуль, используя при этом свойство четности и нечетности функций.

Главная
Алгебра
Презентация по алгебре на тему Четность и нечетность функций

Слайд 112.12.2018
Четность и нечетность функции (Алгебра 9 класс)

Слайд 2 Цель урока: Формирование понятий « четность нечетность функции»;

исследование функций на четность; определение по графику четных и нечетных функций; построение графиков функций, содержащих модуль, используя при этом свойство четности и нечетности функций.

Цель урока: Формирование понятий « четность нечетность функции»; исследование функций на четность; определение

Слайд 31) Область определения функций .
2) Монотонность функции.
3) Ограниченность функции .
4) Наибольшее

и наименьшее значения функции .
5) Непрерывность .
6) Область значений .
7) Выпуклость
8) Четность, нечетность.

Свойства функций

1) Область определения функций .2) Монотонность функции.3) Ограниченность функции .4) Наибольшее и наименьшее значения функции .5) Непрерывность

Слайд 4Запомнить:
Функцию y=f(x), x∈X, называют чётной, если для любого значения x
из множества X выполняется равенство f(−x)=f(x).
График четной функции симметричен относительно

оси х
Функцию y=f(x), x∈X, называют нечётной, если для любого значения x из множества Xвыполняется равенство f(−x)=−f(x).
График нечетной функции симметричен относительно начало координат

Запомнить:Функцию y=f(x), x∈X, называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x). График четной функции симметричен относительно оси хФункцию y=f(x), x∈X, называют нечётной, если для любого значения x из

Слайд 5 Понятие симметричности
Если числовое множество Х вместе с каждым своим

элементом х содержит и противоположный элемент – х, то Х называют симметричным множеством

Понятие симметричности Если числовое множество Х вместе с каждым своим элементом х содержит и противоположный элемент

Слайд 6Определите симметричное множество или нет
(-9; 9),
[ -7; 7],
[0;+

∞ ),
(-∞;+∞ ),
(-20; 5),
[-15; 15)
(-∞;-9),(9;+∞ )
(-∞;-11),[11;+∞ )

Определите симметричное множество или нет (-9; 9), [ -7; 7], [0;+ ∞ ), (-∞;+∞ ), (-20; 5),

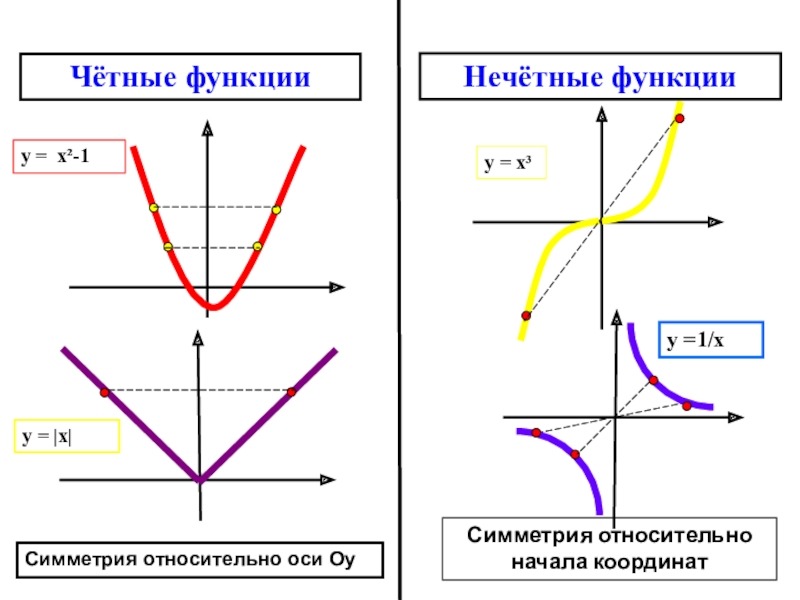
Слайд 7y = x²-1
y = |x|
y = x³
y =1/х
Чётные функции
Нечётные

функции

Симметрия относительно оси Оy

Симметрия относительно
начала координат

Слайд 8Установить , симметрична ли область определения функции
2) Найти f(-x)
3) Сравнить f(-x)

и f(x)
А) если f(-x)=f(x) ¥ x∊D(f), то функция четная
Б) если f(-x)=-f(x) ¥ x∊D(f), то функция нечетная
В) Если хотя бы в одной точке x∊D(f) не выполняются А и Б то функция не является ни четной, ни нечетной

Алгоритм исследования функции на чётность или нечетность