- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Арифметическая и геометрическая прогрессии (9 класс)
Содержание
- 1. Презентация по алгебре на тему Арифметическая и геометрическая прогрессии (9 класс)
- 2. Содержание Понятие арифметической прогрессииФормула n-ого члена а.п.Сумма n первых членов а.п.
- 3. Понятие арифметической прогрессииЧисловую последовательность, каждый член которой,
- 4. Понятие арифметической прогрессии+ d+ d+ d+ d+ d+ d
- 5. Формула n-ого члена арифметической прогрессии– формула n-ого
- 6. Формула n-ого члена арифметической прогрессии– характеристическое свойство а.п.
- 7. Формула суммы n первых членов арифметической
- 8. Формула суммы n первых членов арифметической прогрессии
- 9. Геометрическая прогрессия
- 10. Понятие геометрической прогрессииЧисловую последовательность, все члены которой
- 11. Понятие геометрической прогрессии× q× q× q× q× q× q
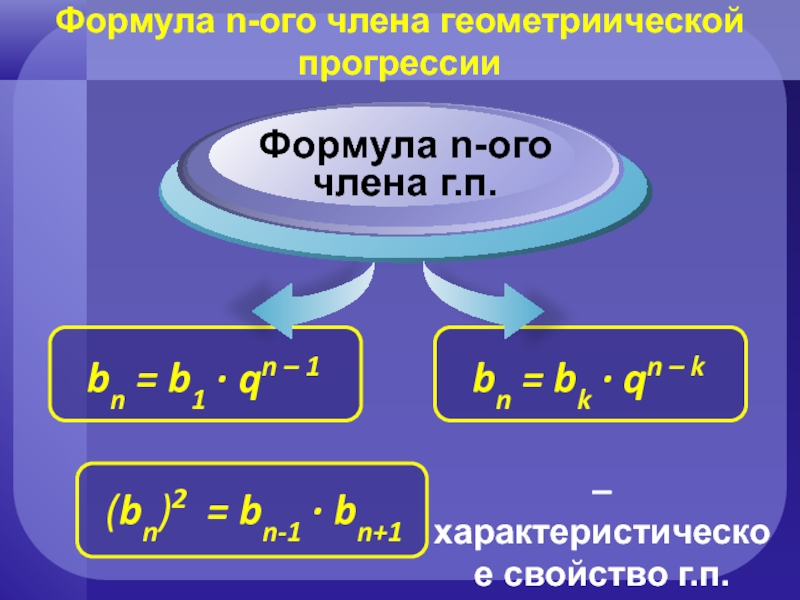
- 12. Формула n-ого члена геометрической прогрессии– формула n-ого
- 13. Формула n-ого члена геометриической прогрессии– характеристическое свойство г.п.
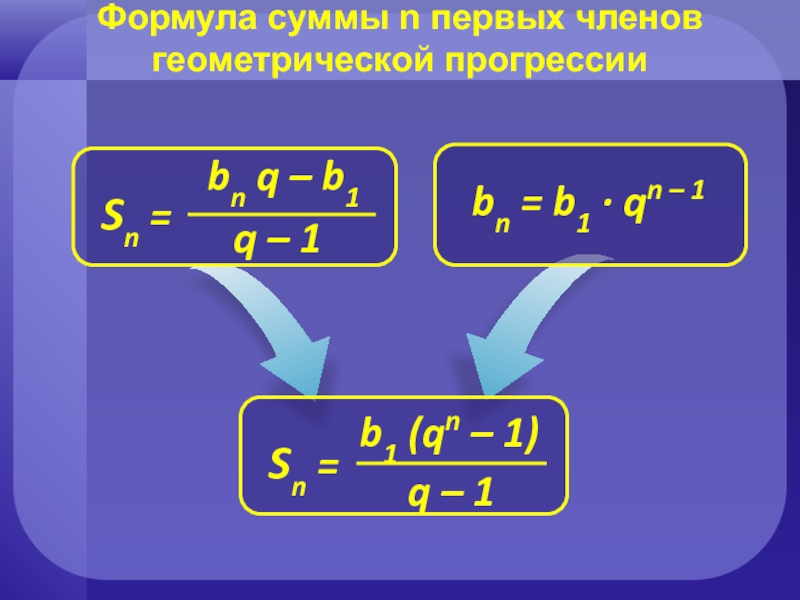
- 14. Формула суммы n первых членов геометрической
- 15. Формула суммы n первых членов геометрической
- 16. Формула суммы n первых членов геометрической прогрессии
- 17. Формула суммы бесконечно убывающей геометрической прогрессииПример:Найти сумму
Слайд 2Содержание
Понятие арифметической прогрессии
Формула n-ого члена а.п.
Сумма n первых членов а.п.
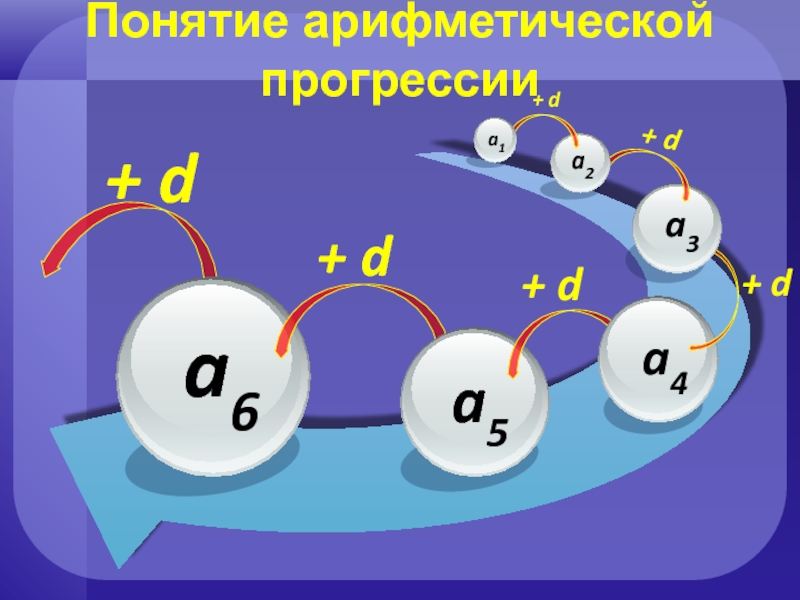
Слайд 3Понятие арифметической прогрессии
Числовую последовательность, каждый член которой, начиная со второго, равен
При этом d, называют разностью арифметической прогрессии.
– рекуррентная формула
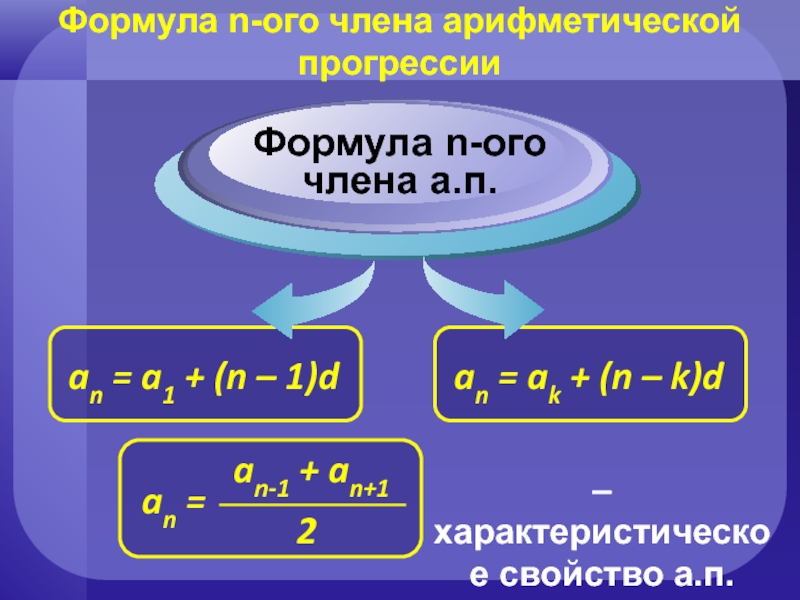
Слайд 5Формула n-ого члена арифметической прогрессии
– формула n-ого члена а.п.
a2 = a1
a1 = a1
a3 = a2 + d = (a1 + d) + d = a1 + 2d
a4 = a3 + d = (a1 + 2d) + d = a1 + 3d
a5 = a4 + d = (a1 + 3d) + d = a1 + 4d
и т.д.
Слайд 7
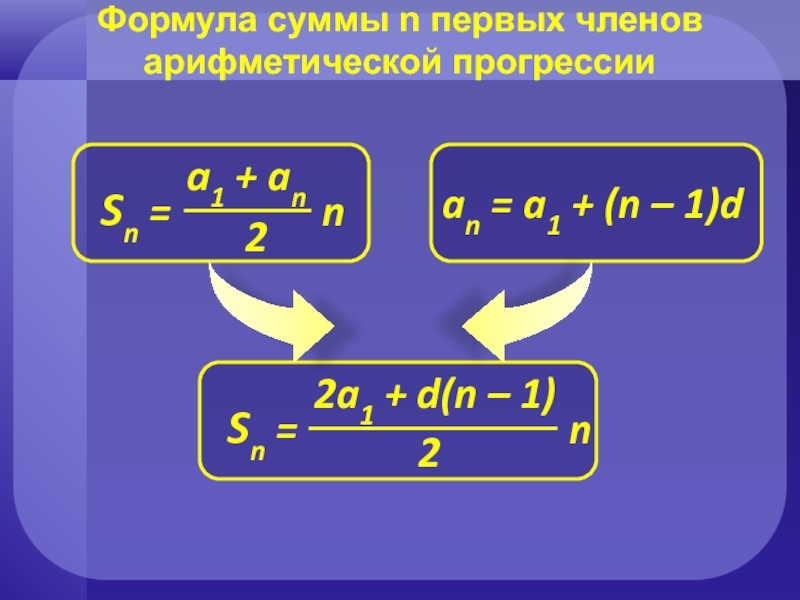
Формула суммы n первых членов
арифметической прогрессии
Sn = a1 + a2
Sn = an + an-1 + an-2 + … + a3 + a2 + a1
2Sn = (a1 + an) + (a2 + an-1) + (a3 + an-2) + …
… + (an-2 + a3) + (an-1 + a2) + (an + a1)
2Sn = (a1 + an)n
+
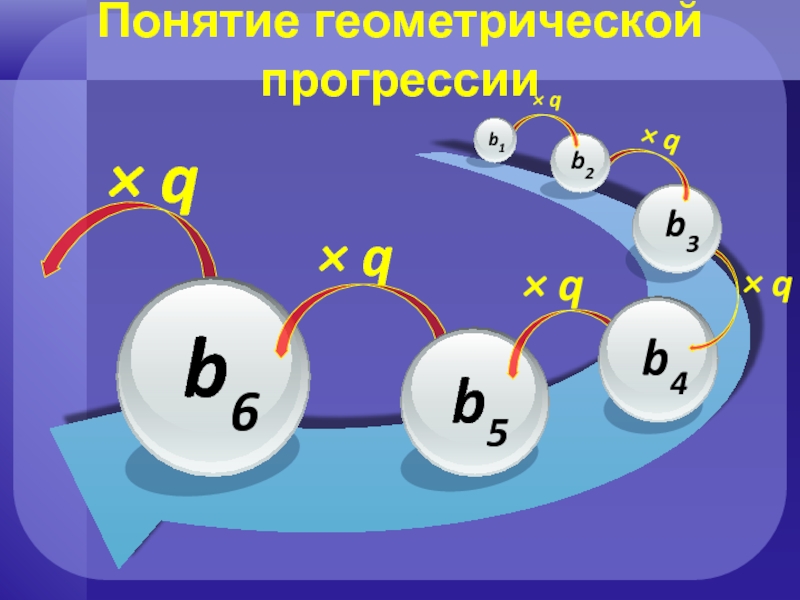
Слайд 10Понятие геометрической прогрессии
Числовую последовательность, все члены которой отличны от нуля и
При этом q, называют знаменателем геометрической прогрессии.
– рекуррентная формула
Слайд 12Формула n-ого члена геометрической прогрессии
– формула n-ого члена г.п.
b2 = b1
b1 = b1
b3 = b2 ∙ q = (b1 ∙ q) ∙ q = b1 ∙ q2
b4 = b3 ∙ q = (b1 ∙ q2) ∙ q = b1 ∙ q3
b5 = b4 ∙ q = (b1 ∙ q3) ∙ q = b1 ∙ q4
и т.д.
Слайд 14
Формула суммы n первых членов
геометрической прогрессии
Sn = b1 + b2
Snq = (b1 + b2 + b3 + … + bn-2 + bn-1 + bn)q
Snq = b1q + b2q + b3q + … + bn-2q + bn-1q +
+ bnq = b2 + b3 + … + bn-1 + bn + bnq
Получим:
Преобразуем:
× q
Слайд 15
Формула суммы n первых членов
геометрической прогрессии
Sn = b1 + (b2
С одной стороны
Snq = (b2 + b3 + … + bn-2 + bn-1 + bn) + bnq
С другой стороны
Вычтем из второго равенства первое
Snq – Sn = bnq – b1
Слайд 17
Формула суммы бесконечно убывающей
геометрической прогрессии
Пример:
Найти сумму бесконечной геометрической прогрессии 12; −4;
В данной прогрессии
q = − 4 : 12 = − 1/3 < 1