- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Методы решения текстовых задач на сплавы и смеси
Содержание
- 1. Презентация по алгебре Методы решения текстовых задач на сплавы и смеси
- 2. Основные методы решения задач на смеси и
- 3. Задача 1. Имеется два сплава меди и
- 4. Задача 1. Имеется два сплава меди и
- 5. «Метод чаш»Каждый из сплавов изображается в виде
- 6. Задача 1. Имеется два сплава меди и
- 7. «Правило креста» или квадрат (конверт)ПирсонаПри расчётах записывают
- 8. Задача 1. Имеется два сплава меди и
- 9. Графический
- 10. Задача 1. Имеется два сплава меди и
- 11. Метод рыбкиЗадача 1. Имеется два сплава меди
- 12. Задача 2. При смешивании первого раствора кислоты,
- 13. Задача 2.При смешивании первого раствора кислоты, концентрация
- 14. Задача 2. При смешивании первого раствора кислоты,
- 15. Задача 3 Первый сплав содержит 5% меди,
- 16. Задача 3 Первый сплав содержит 5% меди,
- 17. Задача 3 Первый сплав содержит 5% меди,
- 18. Задача 4 Смешали некоторое количество 10% раствора
- 19. Задача 5 При смешивании первого раствора соли,
- 20. Задача 5 При смешивании первого раствора соли,
- 21. Задача 5 При смешивании первого раствора
- 22. Задача 6 Имеется два сплава с разным
- 23. Задача 6 Имеется два сплава с разным
- 24. Задача 6 Имеется два сплава с разным
- 25. Задача 7 Имеется два сплава с разным
- 26. Задача 7 Имеется два сплава с разным
- 27. Задача 7 Имеется два сплава
- 28. Задача 8Свежие фрукты содержат 86% воды, а
- 29. Задача 9Свежие фрукты содержат 88% воды, а
- 30. Задача 10 Смешали 10% - ый и
- 31. Задача11. Смешав 70%-й и 60%-й растворы кислоты
Слайд 1Методы решения текстовых задач на сплавы и смеси
Учитель математики МБОУ «СОШ
г. Нефтеюганска Юрьева О.А.
Слайд 2Основные методы решения задач на смеси и сплавы
1) Табличный метод
2) «Метод чаш»
3) «Правило креста»
4) Метод рыбки
5) Графический метод
Рассмотрим решение одной задачи разными методами
Слайд 3
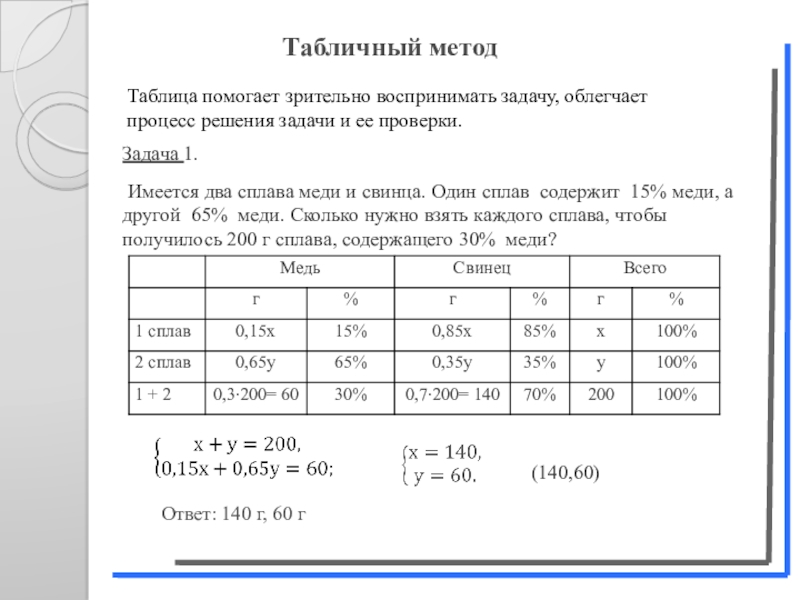
Задача 1.
Имеется два сплава меди и свинца. Один сплав содержит
Ответ: 140 г, 60 г
Табличный метод
(140,60)
Таблица помогает зрительно воспринимать задачу, облегчает процесс решения задачи и ее проверки.
Слайд 4Задача 1.
Имеется два сплава меди и свинца. Один сплав содержит
Вводим одну неизвестную величину.
0,15х + 130 - 0,65х = 60,
х =140,
200-140= 60.
Первого сплава надо взять140г, а второго 60г.
Ответ: 140 г, 60 г
Слайд 5«Метод чаш»
Каждый из сплавов изображается в виде прямоугольника, разбитого на два
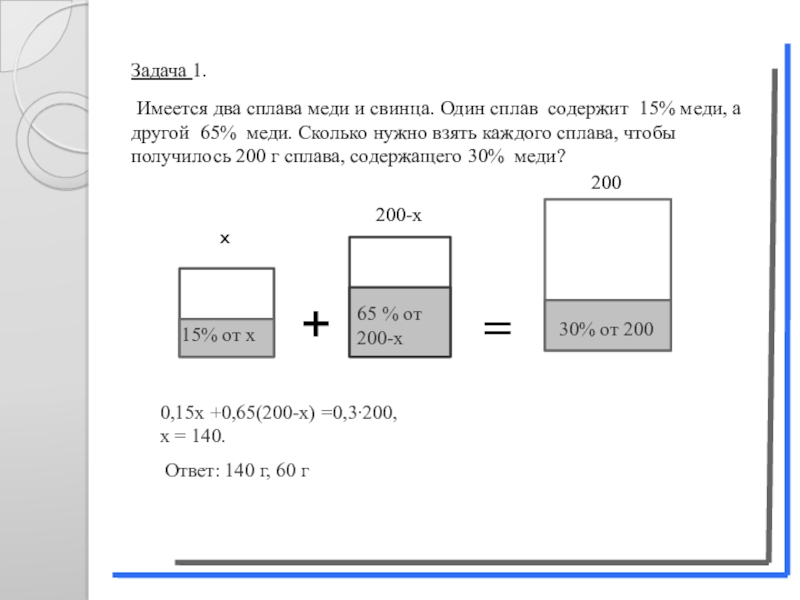
Задача 1.
Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200 г сплава, содержащего 30% меди?
+
=
15% от х
65 % от у
30% от 200
х
у
200
Ответ: 140 г, 60 г
Слайд 6Задача 1.
Имеется два сплава меди и свинца. Один сплав содержит
+
=
15% от х
65 % от 200-х
30% от 200
х
200-х
200
0,15х +0,65(200-х) =0,3∙200,
х = 140.
Ответ: 140 г, 60 г
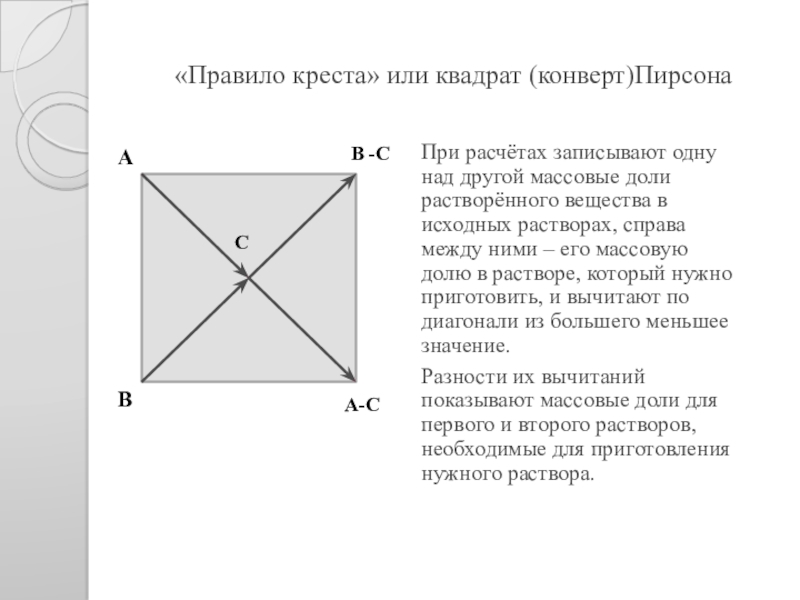
Слайд 7«Правило креста» или квадрат (конверт)Пирсона
При расчётах записывают одну над другой массовые
Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
А
В
В -С
А-С
С
Слайд 8Задача 1.
Имеется два сплава меди и свинца. Один сплав содержит
«Правило креста»
Составляем диагональную схему
1 сплав 0,15 0,3 - 0,15 = 0,15 массовая часть 1сплава
0,3
2 сплав 0,65 0,65 - 0,3 = 0,35 массовая часть 2сплава
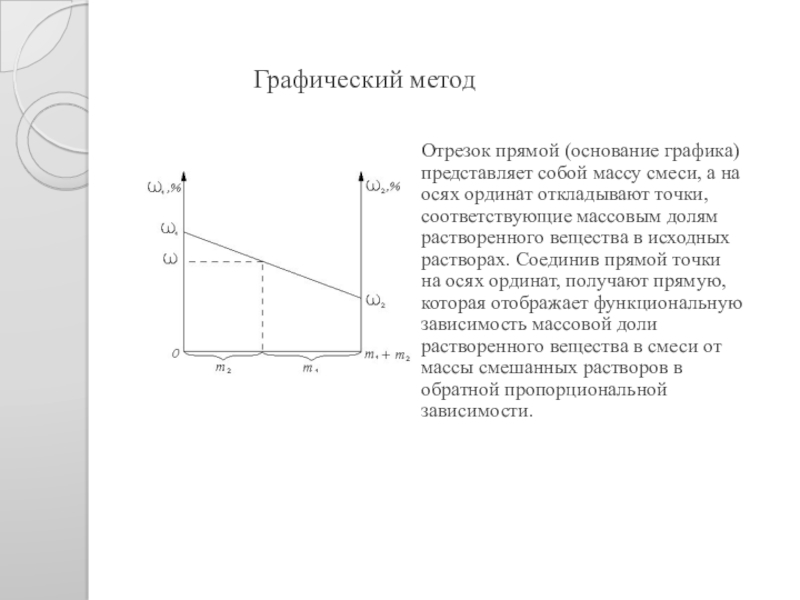
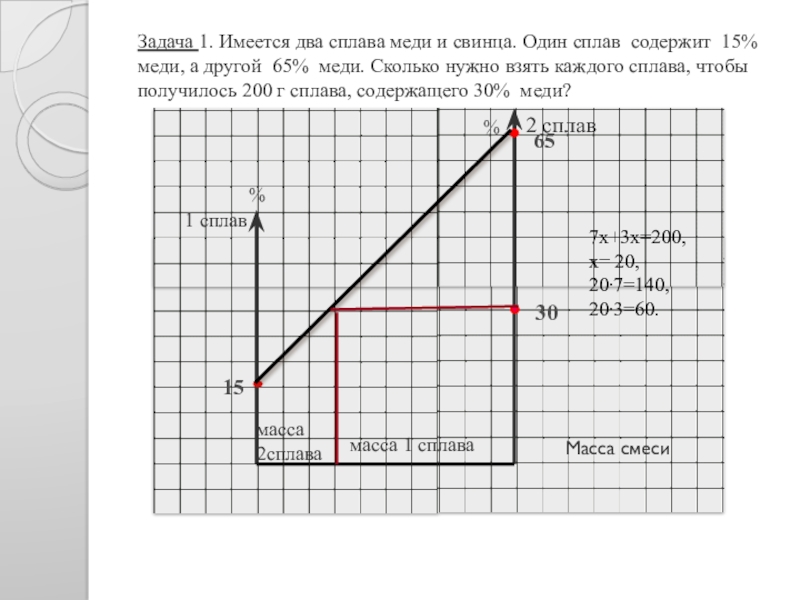
Слайд 9 Графический метод
Отрезок прямой (основание графика)
Слайд 10Задача 1. Имеется два сплава меди и свинца. Один сплав содержит
65
15
30
масса 1 сплава
масса
2сплава
1 сплав
2 сплав
%
%
Масса смеси
7х+3х=200,
х= 20,
20∙7=140,
20∙3=60.
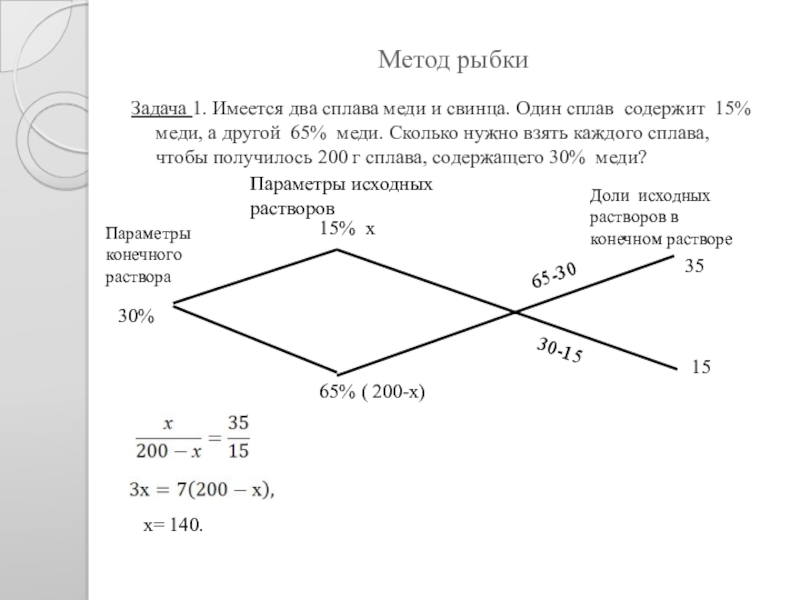
Слайд 11Метод рыбки
Задача 1. Имеется два сплава меди и свинца. Один сплав
Параметры конечного раствора
Параметры исходных растворов
Доли исходных растворов в конечном растворе
30%
15% х
65% ( 200-х)
65-30
30-15
х= 140.
35
15
Слайд 12Задача 2.
При смешивании первого раствора кислоты, концентрация которого 20%, и
Ответ: 2:1
0,2х+0,5у=0,3(х+у),
0,2х+0,5у=0,3х+0,3у,
0,1х=0,2у,
х:у=2:1
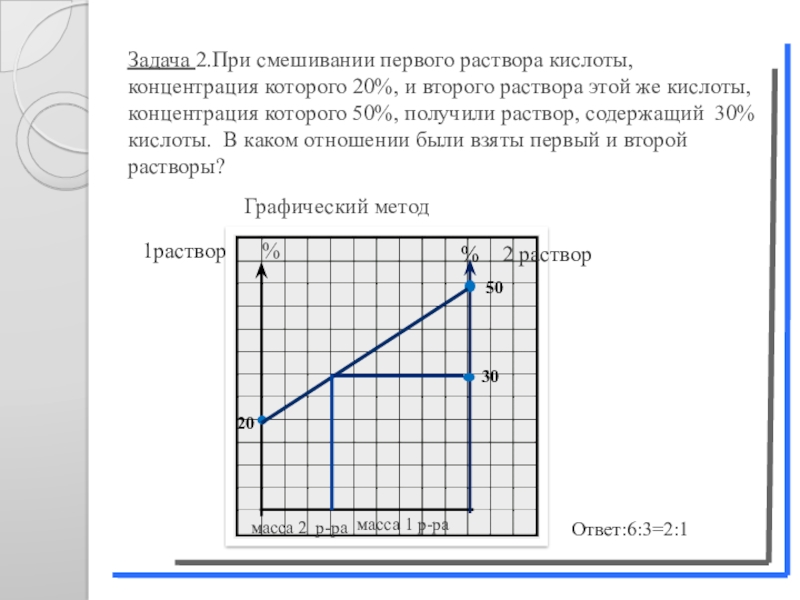
Слайд 13Задача 2.При смешивании первого раствора кислоты, концентрация которого 20%, и второго
Графический метод
20
30
50
% 2 раствор
1раствор %
масса 1 р-ра
масса 2 р-ра
Ответ:6:3=2:1
Слайд 14Задача 2.
При смешивании первого раствора кислоты, концентрация которого 20%, и
«Правила креста»
Составляем диагональную схему
1 раствор 0,2 0,5 - 0,3 = 0,2 массовая часть 1раствора
0,3
2 раствор 0,5 0,3- 0,2 = 0,1 массовая часть 2раствора
Слайд 15Задача 3
Первый сплав содержит 5% меди, второй - 13% меди.
Ответ: 16 кг
0,05х +0,13(х+4) =0,1(2х+4),
х=6.
2∙6+4=16(кг) масса третьего сплава
Слайд 16Задача 3 Первый сплав содержит 5% меди, второй - 13% меди.
13%
5%
10%
масса
1 сплава
масса 2сплава
1 сплав
2 сплав
Слайд 17Задача 3
Первый сплав содержит 5% меди, второй - 13% меди.
«Правила креста»
Составляем диагональную схему
1 раствор 0,05 0,13 - 0,1 = 0,03 массовая часть 1раствора
0,1
2 раствор 0,13 0,1- 0,05 = 0,05 массовая часть 2раствора
5х-3х=4,
2х=4,
х=2.
8∙2=16
Ответ: 16 кг
Слайд 18Задача 4
Смешали некоторое количество 10% раствора некоторого вещества с таким
Ответ: 11%
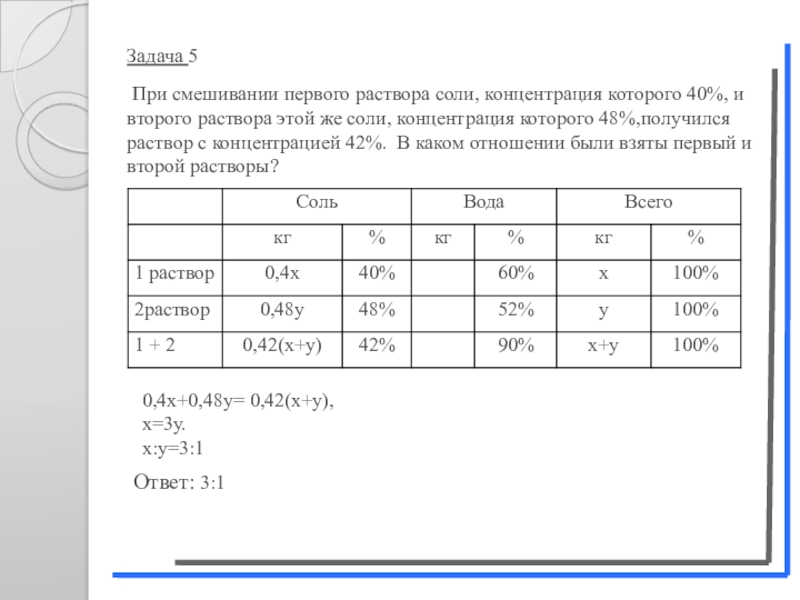
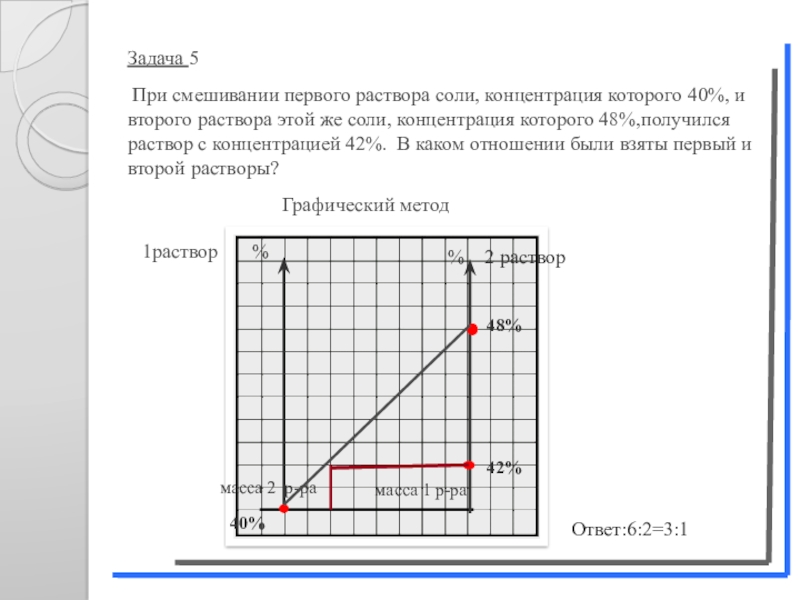
Слайд 19Задача 5
При смешивании первого раствора соли, концентрация которого 40%,
Ответ: 3:1
0,4х+0,48у= 0,42(х+у),
х=3у.
х:у=3:1
Слайд 20Задача 5
При смешивании первого раствора соли, концентрация которого 40%,
Графический метод
40%
42%
48%
% 2 раствор
1раствор %
масса 1 р-ра
масса 2 р-ра
Ответ:6:2=3:1
Слайд 21 Задача 5
При смешивании первого раствора соли, концентрация которого 40%,
«Правила креста»
Составляем диагональную схему
1 раствор 0,4 0,48 - 0,42 = 0,06 массовая часть 1раствора
0,42
2 раствор 0,48 0,42- 0,4 = 0,02 массовая часть 2раствора
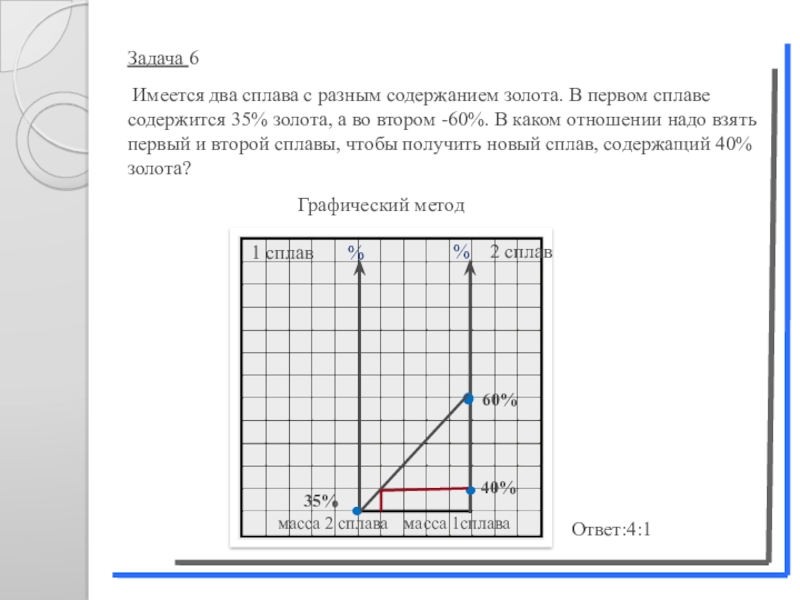
Слайд 22Задача 6
Имеется два сплава с разным содержанием золота. В
Ответ: 4:1
0,35х+0,6у= 0,4(х+у),
5х=20у,
х=4у,
х:у=4:1
Слайд 23Задача 6
Имеется два сплава с разным содержанием золота. В первом
Графический метод
35%
40%
60%
% 2 сплав
1 сплав %
масса 1сплава
масса 2 сплава
Ответ:4:1
Слайд 24Задача 6
Имеется два сплава с разным содержанием золота. В первом
«Правила креста»
Составляем диагональную схему
1 раствор 0,35 0,6 - 0,4 = 0,2 массовая часть 1раствора
0,4
2 раствор 0,6 0,4- 0,35 = 0,05 массовая часть 2раствора
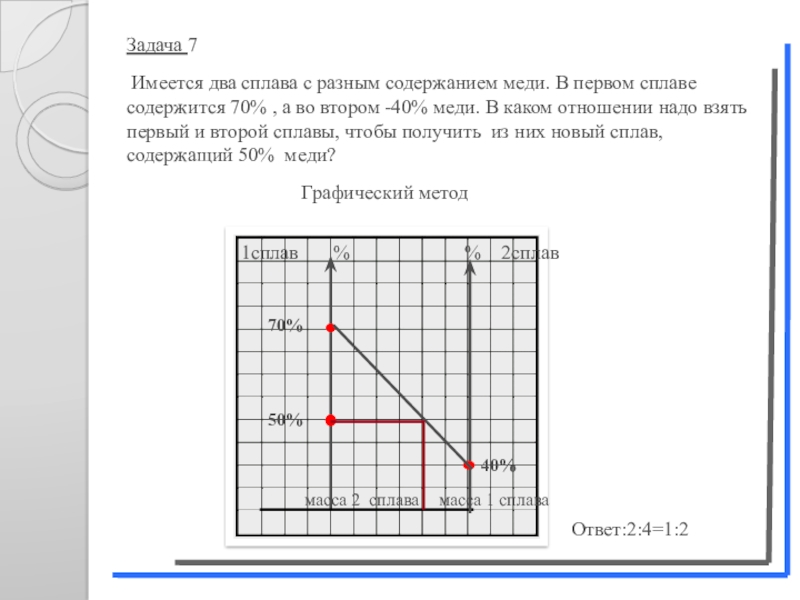
Слайд 25Задача 7
Имеется два сплава с разным содержанием меди. В
Ответ: 1:2
0,7х+0,4у= 0,5(х+у),
0,2х=0,1у,
2х=у,
х:у=1:2
Слайд 26Задача 7
Имеется два сплава с разным содержанием меди. В
Графический метод
40%
50%
70%
% 2сплав
1сплав %
масса 1 сплава
масса 2 сплава
Ответ:2:4=1:2
Слайд 27 Задача 7
Имеется два сплава с разным содержанием
«Правила креста»
Составляем диагональную схему
1 сплав 0,7 0,5 - 0,4 = 0,1 массовая часть 1 сплава
0,5
2 сплав 0,4 0,7- 0,5 = 0,2 массовая часть 2 сплава
Слайд 28Задача 8
Свежие фрукты содержат 86% воды, а высушенные - 23 %.
Решение.
Высушенные фрукты
Пусть х кг сухого вещества содержится в высушенных фруктах
72 кг - 100%
Х кг - 77 % х=77∙72:100=55,44 (кг) сухого вещества.
Свежие фрукты
Пусть у кг потребуется свежих фруктов
55,44 кг – 14 %
у кг - 100%, у = 55,44∙0,14 =396 (кг)
Ответ: 396 кг.
Слайд 29Задача 9
Свежие фрукты содержат 88% воды, а высушенные - 30 %.
Решение.
Высушенные фрукты
Пусть х кг сухого вещества содержится в высушенных фруктах
72 кг - 100%
х кг - 70 %, х = 0,7∙72 = 50,4 (кг) сухого вещества.
Свежие фрукты
Пусть у кг потребуется свежих фруктов
50,4 кг - 12 %
у кг - 100%, у = 50,4∙100:12=420(кг) свежих фруктов потребуется
Ответ: 420
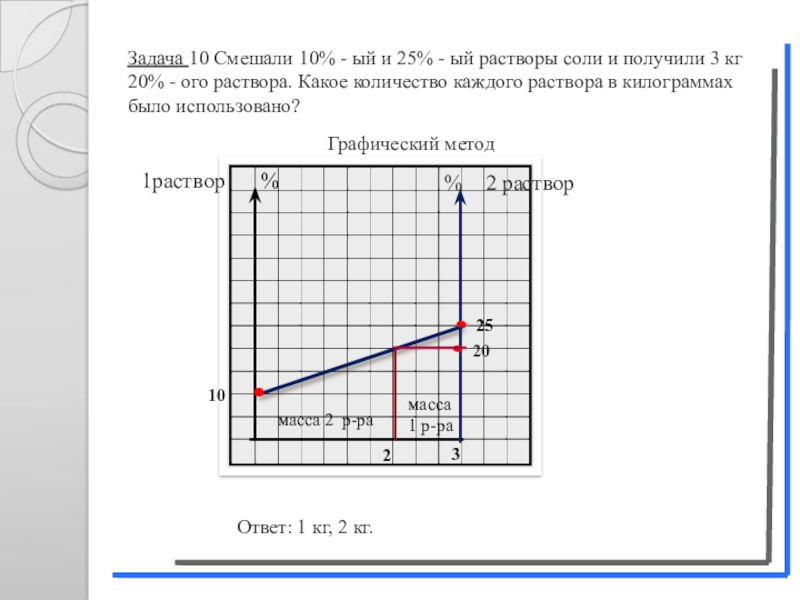
Слайд 30Задача 10 Смешали 10% - ый и 25% - ый растворы
Графический метод
10
20
25
2
3
% 2 раствор
1раствор %
масса 1 р-ра
масса 2 р-ра
Ответ: 1 кг, 2 кг.
Слайд 31Задача11. Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг
2х +у = 10.
у = 4
Тогда х = 3
Ответ: 3 кг