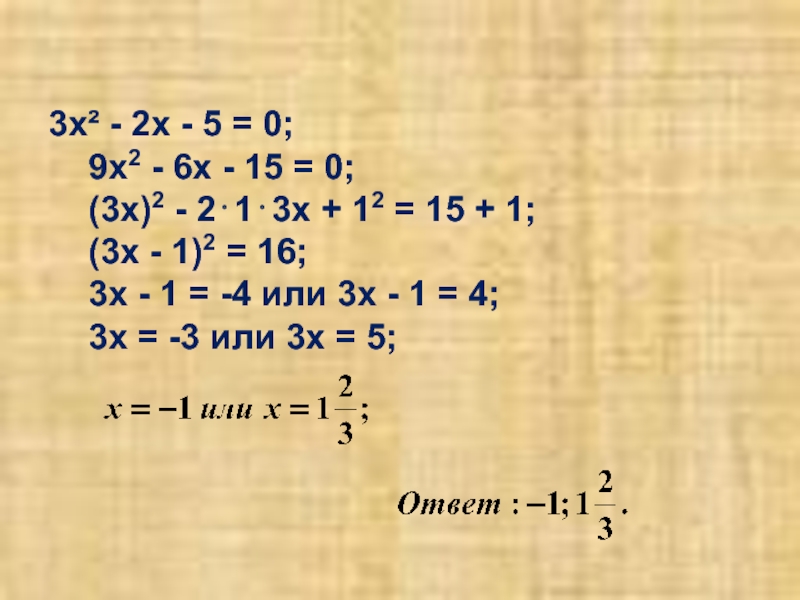- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Метод выделения полного квадрата 8 класс.
Содержание
- 1. Презентация по алгебре Метод выделения полного квадрата 8 класс.
- 2. Для решения квадратных уравнений применяется метод выделения
- 3. х²-10х+16 =0;х²- 10х= -16;х² -10х+25= -16+25;(х-5)²= 9;х-5=3
- 4. 25х²-10х-3=0;25х² - 10х = 3;25х² -10х +
- 5. х²- 3х-10 = 0;х² - 3х =
- 6. 5х²- 7х- 6 = 0;25х² - 35х
- 7. 3х² - 2х - 5 = 0; 9х2
- 8. Спасибо за урок!
Для решения квадратных уравнений применяется метод выделения полного квадрата.Например:х²+4х-12=0;х²+4х=12;х²+4х+4=12+4;(х+2)²=16;х+2=4 или х+2=-4;х=2 х=-6;Ответ: -6; 2.
Слайд 2Для решения квадратных уравнений применяется метод выделения полного квадрата.
Например:
х²+4х-12=0;
х²+4х=12;
х²+4х+4=12+4;
(х+2)²=16;
х+2=4 или х+2=-4;
х=2
х=-6;
Ответ: -6; 2.
Слайд 3х²-10х+16 =0;
х²- 10х= -16;
х² -10х+25= -16+25;
(х-5)²= 9;
х-5=3 или х-5= -3;
х=8
х=2;
Ответ: 2; 8.
Слайд 425х²-10х-3=0;
25х² - 10х = 3;
25х² -10х + 1=3+1;
(5х-1)² =4;
5х-1=2 или 5х-1=
-2;
5х=3 5х= -1;
х = 0,6 х = -0,2;
5х=3 5х= -1;
х = 0,6 х = -0,2;
Ответ: -0,2; 0,6.
Слайд 5х²- 3х-10 = 0;
х² - 3х = 10;
х² - 3х +2,25
= 10+ 2,25;
(х – 1,5)² = 12,25;
х- 1,5 = 3,5 или х- 1,5 = -3,5;
х = 5 х = -2;
(х – 1,5)² = 12,25;
х- 1,5 = 3,5 или х- 1,5 = -3,5;
х = 5 х = -2;
Ответ: -2; 5.
Слайд 65х²- 7х- 6 = 0;
25х² - 35х - 30 = 0;
(5х)²
- 2⋅3,5⋅5х + (3,5)2 = 30 + 12,25;
(5х – 3,5)² = 42,25;
5х - 3,5 = 6,5 или 5х - 3,5 = - 6,5;
5х = 10 5х = -3;
х = 2 х = -0,6;
(5х – 3,5)² = 42,25;
5х - 3,5 = 6,5 или 5х - 3,5 = - 6,5;
5х = 10 5х = -3;
х = 2 х = -0,6;
Ответ: -0,6; 2.
Слайд 73х² - 2х - 5 = 0;
9х2 - 6х - 15
= 0;
(3х)2 - 2⋅1⋅3х + 12 = 15 + 1;
(3х - 1)2 = 16;
3х - 1 = -4 или 3х - 1 = 4;
3х = -3 или 3х = 5;
(3х)2 - 2⋅1⋅3х + 12 = 15 + 1;
(3х - 1)2 = 16;
3х - 1 = -4 или 3х - 1 = 4;
3х = -3 или 3х = 5;