Адыгея
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа на тему График гармонического колебания (10 класс)
Содержание
Гармонические колебания y = A sin (ωt + α) –уравнение гармонических колебанийилизакон гармонических колебаний(А – амплитуда колебаний (максимальное отклонение от положения равновесия), ω - частота колебаний, α - начальная фаза колебаний)
Слайд 1Тригонометрические функции
График гармонического колебания
Нигматуллин Радий Радиевич
МБОУ СШ №24 а. Шенджий,
Республика
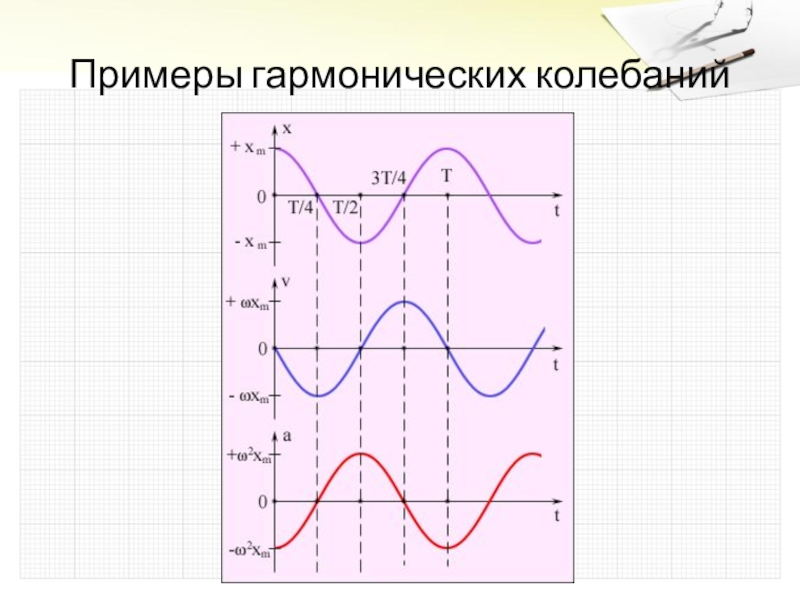
Слайд 2Гармонические колебания
y = A sin (ωt + α) –
уравнение гармонических
колебаний
или
закон гармонических колебаний
(А – амплитуда колебаний (максимальное отклонение от положения равновесия), ω - частота колебаний, α - начальная фаза колебаний)
или
закон гармонических колебаний
(А – амплитуда колебаний (максимальное отклонение от положения равновесия), ω - частота колебаний, α - начальная фаза колебаний)
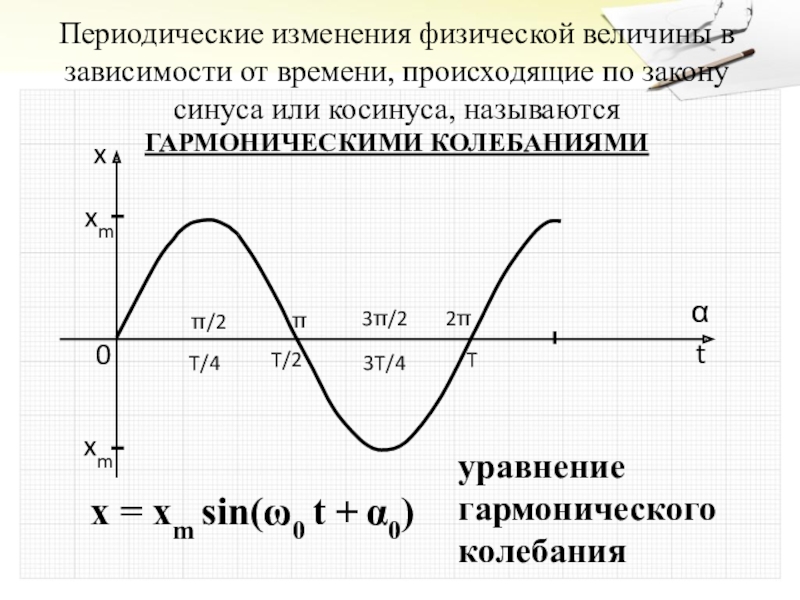
Слайд 3Периодические изменения физической величины в зависимости от времени, происходящие по закону
синуса или косинуса, называются ГАРМОНИЧЕСКИМИ КОЛЕБАНИЯМИ
x = xm sin(ω0 t + α0)
уравнение гармонического колебания
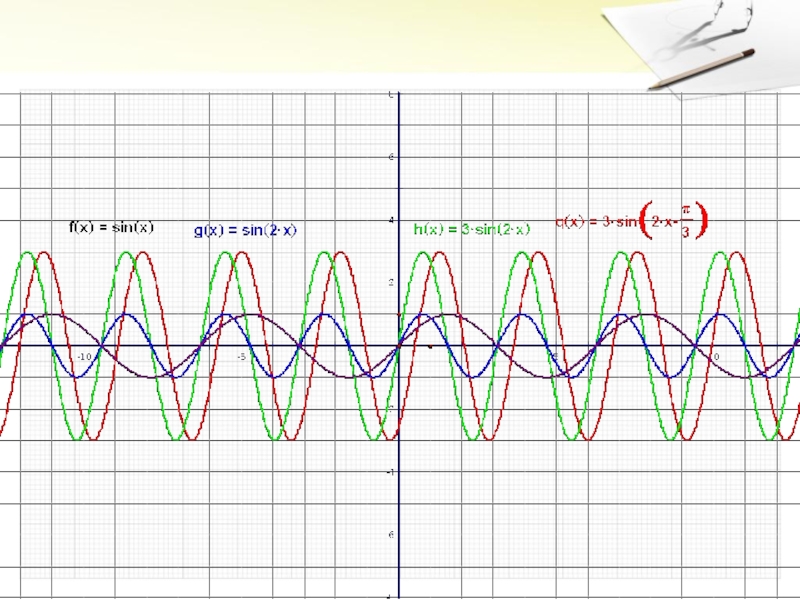
Слайд 5Построить график функции
в системе координат sOt.
s = sint
Cжать синусоиду к
оси ординат с коэффициентом 2.
Растянуть синусоиду от оси абсцисс с коэффициентом 3.
Сжатую и растянутую синусоиду сдвинуть вдоль оси абсцисс на влево.
Растянуть синусоиду от оси абсцисс с коэффициентом 3.
Сжатую и растянутую синусоиду сдвинуть вдоль оси абсцисс на влево.