Презентация, доклад по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значения непрерывной функции на заданном отрезке (10 класс)

Содержание

1. Презентация по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значения непрерывной функции на заданном отрезке (10 класс)
2. Правильному применению методов можно научиться только применяя их на разнообразных примерах.Цейтен Г.Г.
3. Найдите производные данных функций
4. Слайд 4
5. Для функции
6. Вейерштрасс Карл Теодор Вильгельм
7. yнаиб= f(а), а – конец отрезкаyнаим= f(с),
8. Найти наибольшее и наименьшее значение функции y=f(x)
9. Найти наибольшее и наименьшее значение функции y=f(x)
10. Обобщениеyнаиб= f(а), а – конец отрезкаyнаим= f(с),
11. Алгоритм нахождения наименьшего и наибольшего непрерывной функции
12. Для функции
13. Домашнее задание§ 46 разобрать пример №2.Выучить алгоритм нахождения наибольшего и наименьшего значения функции.Упражнения №46.9(б),46.15(в),46.11
14. Решите самостоятельно:f(x)=|x-3|-2 на отрезке [1;4]
15. Решения1В.f(x)=3х2-2х3+1 x∈Rf’(x)=6x-6x2
16. “…Особенную важность имеют те методы науки, которые
17. Рефлексия

Правильному применению методов можно научиться только применяя их на разнообразных примерах.Цейтен Г.Г.

Главная
Алгебра
Презентация по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значения непрерывной функции на заданном отрезке (10 класс)

Слайд 1Отыскание наибольшего и наименьшего значений непрерывной функции не промежутке

Слайд 2Правильному применению методов можно научиться только применяя их на разнообразных примерах.
Цейтен

Г.Г.

Слайд 3Найдите производные данных функций

Слайд 4

Слайд 5Для функции найдите:
а) наименьшее значение на отрезке [-1;4];

б) наибольшее значение на отрезке [-1;4].

Для функции найдите: а) наименьшее значение на отрезке [-1;4]; б)

Слайд 6Вейерштрасс Карл Теодор Вильгельм

(1815-1897 гг.) - немецкий математик

Теорема Вейерштрасса

Непрерывная на отрезке [a;b] функция f принимает на этом отрезке наибольшее и наименьшее значения.

Вейерштрасс Карл Теодор Вильгельм (1815-1897

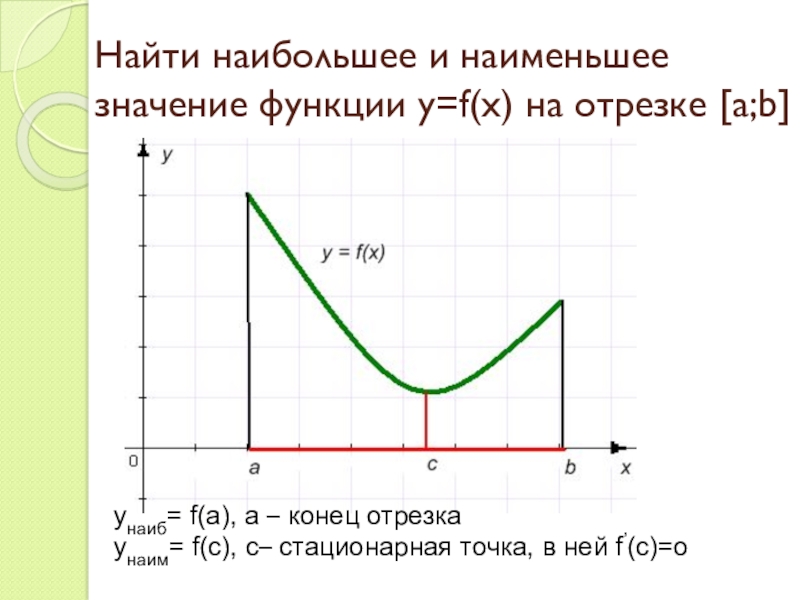
Слайд 7yнаиб= f(а), а – конец отрезка
yнаим= f(с), с– стационарная точка, в

ней f’(с)=о

Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [a;b]

Слайд 8Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [a;b]
Унаим=f(а), а

– конец отрезка
Унаиб= f(m), m– стационарная точка, в ней f’(m)=о

Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [a;b]Унаим=f(а), а – конец отрезкаУнаиб= f(m), m– стационарная

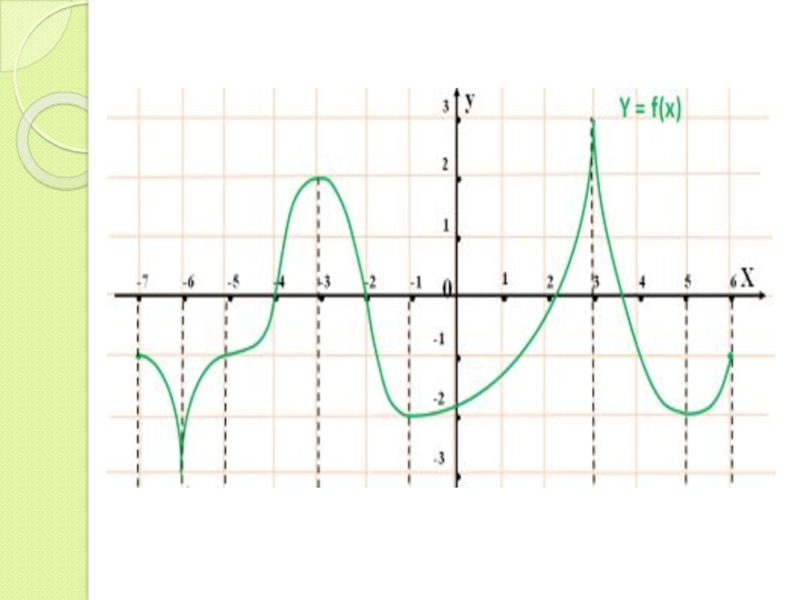
Слайд 9Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [-2;6]
Унаим=f(-1)=f(5), x=-1,

x=5 – стационарные точки
Унаиб= f(3), х=3– критическая точка, в ней f’(3) не существует

Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [-2;6]Унаим=f(-1)=f(5), x=-1, x=5 – стационарные точкиУнаиб= f(3), х=3–

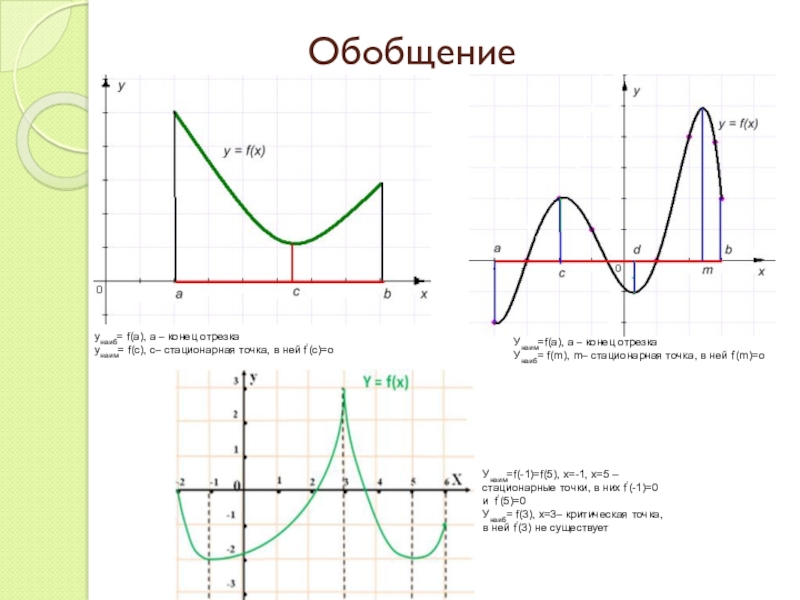
Слайд 10Обобщение
yнаиб= f(а), а – конец отрезка
yнаим= f(с), с– стационарная точка, в

ней f’(с)=о

Унаим=f(а), а – конец отрезка
Унаиб= f(m), m– стационарная точка, в ней f’(m)=о

Унаим=f(-1)=f(5), x=-1, x=5 – стационарные точки, в них f’(-1)=0 и f’(5)=0
Унаиб= f(3), х=3– критическая точка, в ней f’(3) не существует

Обобщениеyнаиб= f(а), а – конец отрезкаyнаим= f(с), с– стационарная точка, в ней f’(с)=оУнаим=f(а), а – конец отрезкаУнаиб=

Слайд 11Алгоритм нахождения наименьшего и наибольшего непрерывной функции y=f(x) на отрезке [a;b]

Найти производную f’(x).
Найти стационарные и критические точки функции, лежащие внутри отрезка [a;b].
Вычислить значения функции y=f(x) в точках, отобранных на втором шаге, в точка a и b; выбрать среди этих значений наименьшее (это будет Унаим) и наибольшее (это будет Унаиб).

Алгоритм нахождения наименьшего и наибольшего непрерывной функции y=f(x) на отрезке [a;b] Найти производную f’(x).Найти стационарные и критические

Слайд 12Для функции найдите:
а) наименьшее значение на отрезке [-1;4];

б) наибольшее значение на отрезке [-1;4].

Слайд 13Домашнее задание
§ 46 разобрать пример №2.
Выучить алгоритм нахождения наибольшего и наименьшего

значения функции.
Упражнения №46.9(б),46.15(в),46.11

Слайд 14Решите самостоятельно:
f(x)=|x-3|-2 на отрезке [1;4]

Слайд 15Решения
1В.f(x)=3х2-2х3+1 x∈R
f’(x)=6x-6x2 x∈R
критических

точек нет
f’(x)=0
6x-6x2 =0
x-x2 =0
x(x-1)=0
x=0 или x=1
y(-1)=6
y(4)=79
y(0)=1
y(1)=2
Ответ: yнаим=1, унаиб=79

11В.f(x)=9x+3х2-х3 x∈R
f’(x)=9+6x-3x2 x∈R
критических точек нет
f’(x)=0
9+6x-3x2 =0
3x2-6x-9=0
X2-2x-3=0
x=-1 или x=3 ∉[-2;2]
y(-2)=2
y(2)=22
y(-1)=-5
Ответ: yнаим=-5, унаиб=22

Решения1В.f(x)=3х2-2х3+1 x∈Rf’(x)=6x-6x2 x∈Rкритических точек нетf’(x)=06x-6x2 =0x-x2 =0x(x-1)=0x=0 или x=1y(-1)=6y(4)=79y(0)=1y(1)=2Ответ:

Слайд 16“…Особенную важность имеют те методы науки, которые позволяют решать задачу, общую

для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды”.

Чебышев Пафнутий Львович (1821-1894), знаменитый русский математик, основатель Петербуржской математической школы

“…Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как

Слайд 17Рефлексия

Скачать презентацию

Презентация, доклад по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значения непрерывной функции на заданном отрезке (10 класс)

Содержание

Слайд 1Отыскание наибольшего и наименьшего значений непрерывной функции не промежутке

Слайд 2Правильному применению методов можно научиться только применяя их на разнообразных примерах.
Цейтен

Слайд 3Найдите производные данных функций

Слайд 4

Слайд 5Для функции найдите:
а) наименьшее значение на отрезке [-1;4];

Слайд 6Вейерштрасс Карл Теодор Вильгельм

Слайд 7yнаиб= f(а), а – конец отрезка
yнаим= f(с), с– стационарная точка, в

Слайд 8Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [a;b]
Унаим=f(а), а

Слайд 9Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [-2;6]
Унаим=f(-1)=f(5), x=-1,

Слайд 10Обобщение
yнаиб= f(а), а – конец отрезка
yнаим= f(с), с– стационарная точка, в

Слайд 11Алгоритм нахождения наименьшего и наибольшего непрерывной функции y=f(x) на отрезке [a;b]

Слайд 12Для функции найдите:
а) наименьшее значение на отрезке [-1;4];

Слайд 13Домашнее задание
§ 46 разобрать пример №2.
Выучить алгоритм нахождения наибольшего и наименьшего

Слайд 14Решите самостоятельно:
f(x)=|x-3|-2 на отрезке [1;4]

Слайд 15Решения
1В.f(x)=3х2-2х3+1 x∈R
f’(x)=6x-6x2 x∈R
критических

Слайд 16“…Особенную важность имеют те методы науки, которые позволяют решать задачу, общую

Слайд 17Рефлексия

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значения непрерывной функции на заданном отрезке (10 класс)

Содержание

Слайд 1Отыскание наибольшего и наименьшего значений непрерывной функции не промежутке

Слайд 2Правильному применению методов можно научиться только применяя их на разнообразных примерах.Цейтен

Слайд 3Найдите производные данных функций

Слайд 4

Слайд 5Для функции найдите: а) наименьшее значение на отрезке [-1;4];

Слайд 6Вейерштрасс Карл Теодор Вильгельм

Слайд 7yнаиб= f(а), а – конец отрезкаyнаим= f(с), с– стационарная точка, в

Слайд 8Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [a;b]Унаим=f(а), а

Слайд 9Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [-2;6]Унаим=f(-1)=f(5), x=-1,

Слайд 10Обобщениеyнаиб= f(а), а – конец отрезкаyнаим= f(с), с– стационарная точка, в

Слайд 11Алгоритм нахождения наименьшего и наибольшего непрерывной функции y=f(x) на отрезке [a;b]

Слайд 12Для функции найдите: а) наименьшее значение на отрезке [-1;4];

Слайд 13Домашнее задание§ 46 разобрать пример №2.Выучить алгоритм нахождения наибольшего и наименьшего

Слайд 14Решите самостоятельно:f(x)=|x-3|-2 на отрезке [1;4]

Слайд 15Решения1В.f(x)=3х2-2х3+1 x∈Rf’(x)=6x-6x2 x∈Rкритических

Слайд 16“…Особенную важность имеют те методы науки, которые позволяют решать задачу, общую

Слайд 17Рефлексия

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 2Правильному применению методов можно научиться только применяя их на разнообразных примерах.
Цейтен

Слайд 5Для функции найдите:
а) наименьшее значение на отрезке [-1;4];

Слайд 7yнаиб= f(а), а – конец отрезка
yнаим= f(с), с– стационарная точка, в

Слайд 8Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [a;b]
Унаим=f(а), а

Слайд 9Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [-2;6]
Унаим=f(-1)=f(5), x=-1,

Слайд 10Обобщение
yнаиб= f(а), а – конец отрезка
yнаим= f(с), с– стационарная точка, в

Слайд 12Для функции найдите:
а) наименьшее значение на отрезке [-1;4];

Слайд 13Домашнее задание
§ 46 разобрать пример №2.
Выучить алгоритм нахождения наибольшего и наименьшего

Слайд 14Решите самостоятельно:
f(x)=|x-3|-2 на отрезке [1;4]

Слайд 15Решения
1В.f(x)=3х2-2х3+1 x∈R
f’(x)=6x-6x2 x∈R
критических