Тема урока:
«Производная показательной функции».
Сердюков В. И. - учитель математики МОУ СОШ №3 г. Карасука Новосибирской области
2008 г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа Производная показательной функции (11 класс)
Содержание
- 1. Презентация по алгебре и началам анализа Производная показательной функции (11 класс)
- 2. Цели урока. Обучающие: введение понятие числа е;
- 3. Оборудование урока. Учебник: Алгебра и начала
- 4. План урока.I. Оргмомент.II. Актуализация знаний.III. Изучение
- 5. I. Постановка цели.Объявляется тема урока: «Производная показательной
- 6. II. Актуализация знанийВопрос1. Как связаны между собой
- 7. Ответ на вопрос 1.
- 8. Вопрос 2. График какой функции изображен на рисунке?
- 9. Ответ на вопрос 2. График какой функции
- 10. Вопрос 3Как геометрически определить значение производной функции в точке х=0?
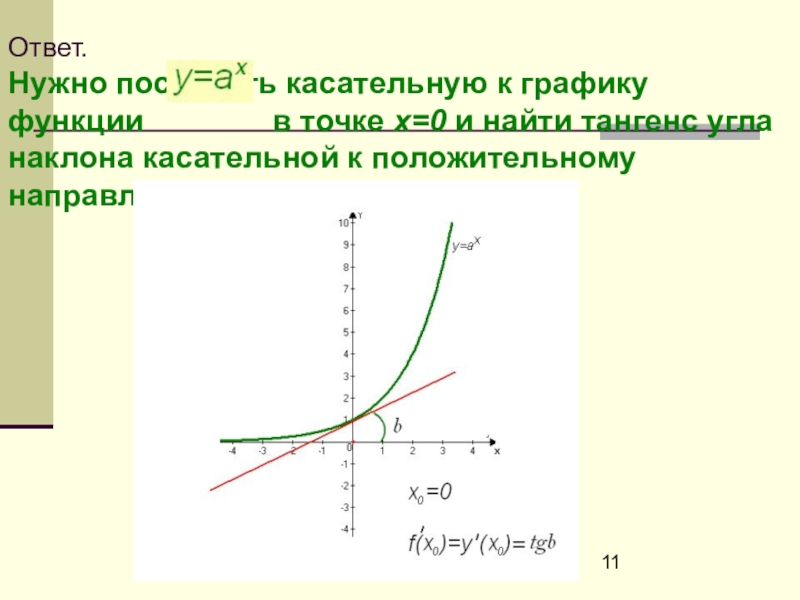
- 11. Ответ. Нужно построить касательную к графику
- 12. III. Изучение нового материала На сегодняшнем уроке
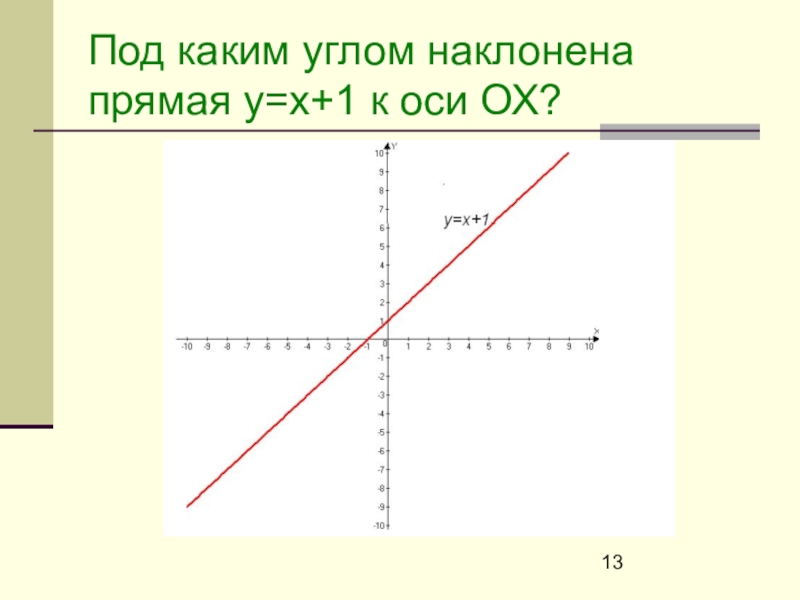
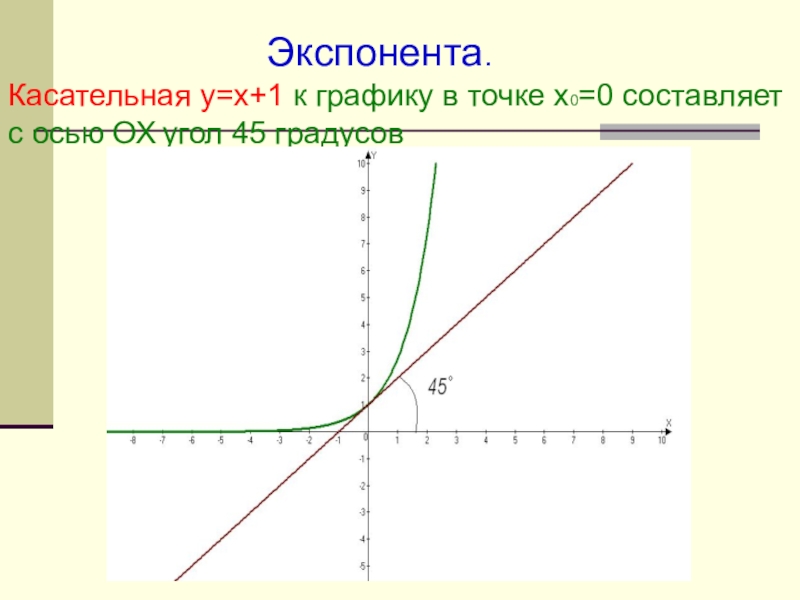
- 13. Под каким углом наклонена прямая y=x+1 к оси ОХ?
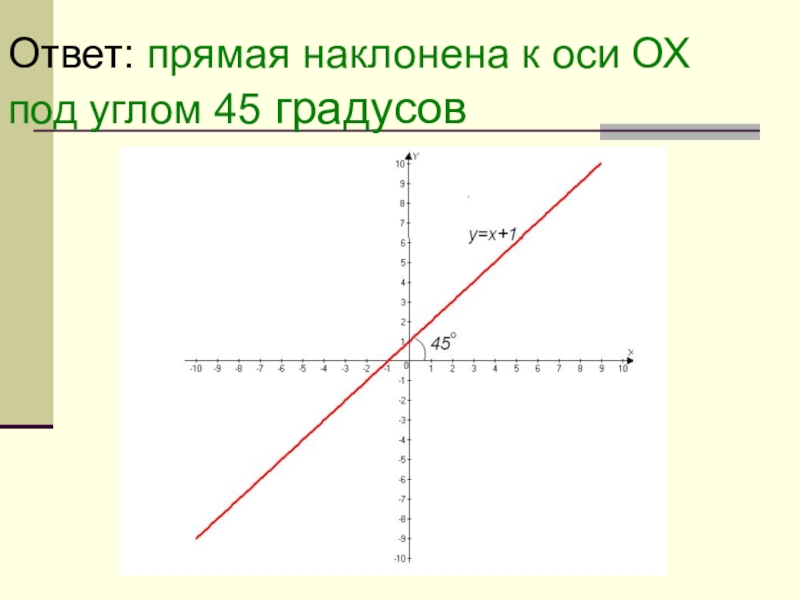
- 14. Ответ: прямая наклонена к оси ОХ под углом 45 градусов
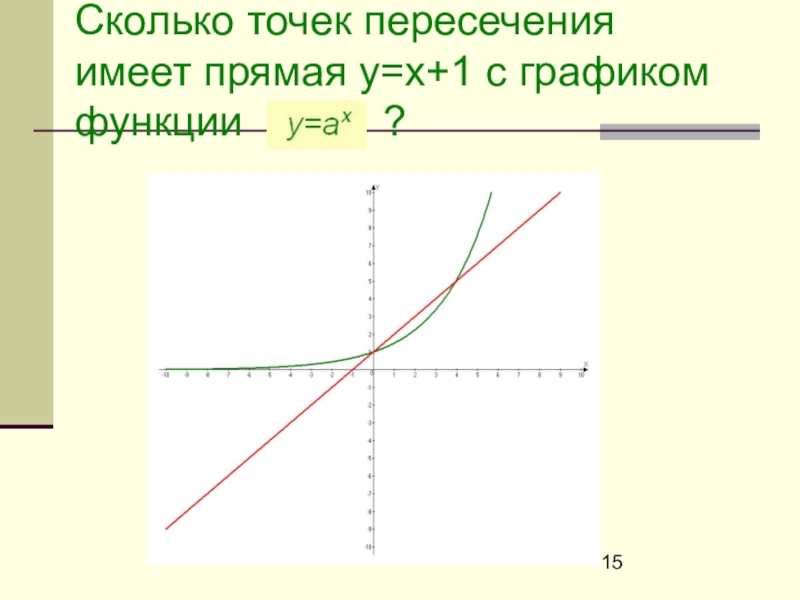
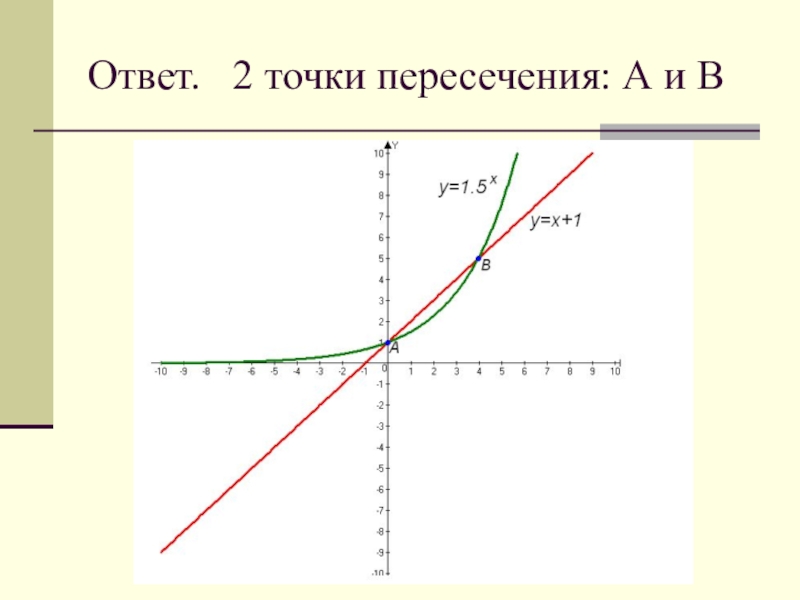
- 15. Сколько точек пересечения имеет прямая у=х+1 с графиком функции ?
- 16. Ответ. 2 точки пересечения: А и В
- 17. Исследовательская практическая работа за компьютером Примечание. На
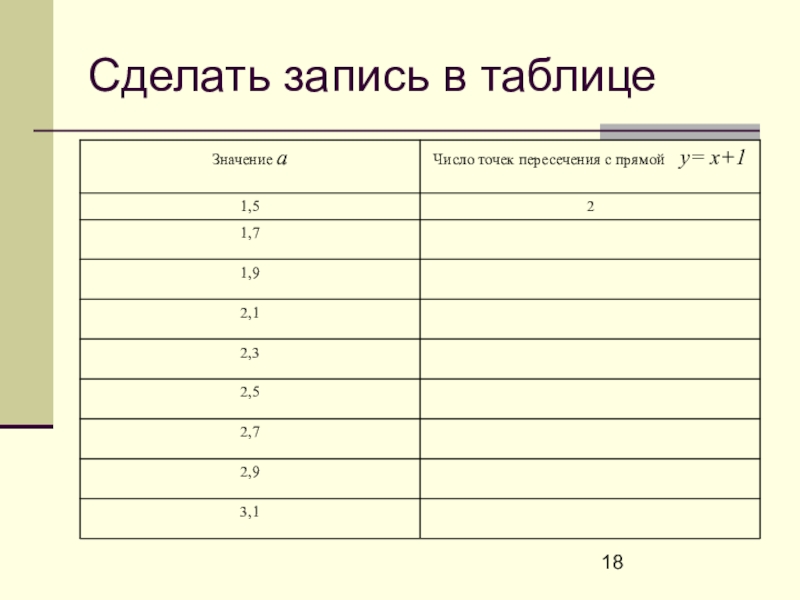
- 18. Сделать запись в таблице
- 19. 4. Проделать пункты 1, 2. и 3.
- 20. При каком а для функции выполняется условие: у´(о)= tg45=1 ?Ответ : при а=2,7
- 21. ТеоремаПримем без доказательства теорему:Существует такое число больше
- 22. В анализе доказано, что число e иррациональное.
- 23. Слайд 23
- 24. Формулы дифференцирования
- 25. Образцы выполнения упражнений
- 26. Закрепление.Выполнить упражнения №538-540 (а,б)
- 27. V. Проверочная работа
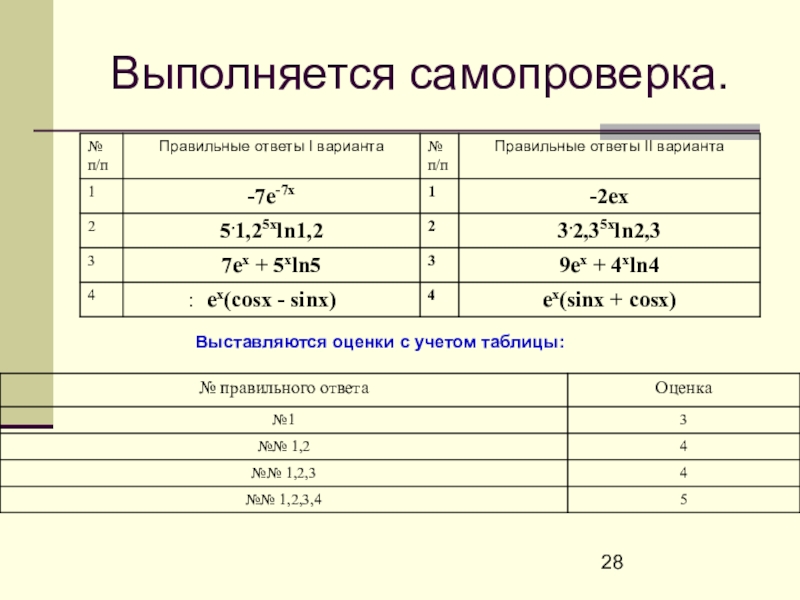
- 28. Выполняется самопроверка. Выставляются оценки с учетом таблицы::
- 29. VI. Итог урока.Выясняется (поднятием рук), какие учащиеся
- 30. Как вы поняли, что такое число е?e - иррациональное число. е ≈ 2,7 .
- 31. VII. Домашнее заданиеп.41. Прочитать. Выучить формулы и
- 32. ЛитератураАЛГЕБРА И НАЧАЛА АНАЛИЗАУчебник для 10-11 классов
Цели урока. Обучающие: введение понятие числа е; изучение формул дифференцирования (без доказательства); показать применение этих формул при решении упражнений на дифференцирование функций; получение
Слайд 1 Алгебра и
начала анализа. 11класс. Базовый уровень
Слайд 2Цели урока.
Обучающие: введение понятие числа е; изучение формул дифференцирования
(без доказательства); показать применение этих формул при решении упражнений на дифференцирование функций; получение информации путем создания математической модели с помощью приложения Advanced Grapher.
Развивающие: развитие мышления, внимания, способности делать выводы из практического эксперимента.
Воспитывающие: воспитание наблюдательности, аккуратности , настойчивости
Развивающие: развитие мышления, внимания, способности делать выводы из практического эксперимента.
Воспитывающие: воспитание наблюдательности, аккуратности , настойчивости
Слайд 3
Оборудование урока.
Учебник: Алгебра и начала анализа 10-11 (под редакцией А. Н.Колмогорова)
2006 г.
Листы с «Инструкцией к выполнению практической работы». (см. слайды 17-20)
Слайды с рисунками по теме урока (в данной презентации).
Компьютеры.
Прикладная компьютерная среда Advanced Grapher.
Мультимедийный проектор.
Листы с «Инструкцией к выполнению практической работы». (см. слайды 17-20)
Слайды с рисунками по теме урока (в данной презентации).
Компьютеры.
Прикладная компьютерная среда Advanced Grapher.
Мультимедийный проектор.
Слайд 4
План урока.
I. Оргмомент.
II. Актуализация знаний.
III. Изучение нового материала.
Постановка задачи исследовательской работы.
Исследовательская
практическая работа за компьютерами.
Вывод.
Понятие числа e. Понятие экспоненты, натурального логарифма.
Формулы дифференцирования показательной функции.
IV. Закрепление изученного материала.
Разбор образцов примеров на нахождение производной показательной функции.
Решение упражнений из учебника.
V. Срезовая работа.
VI. Итог урока. Оценки.
VII. Домашнее задание.
Вывод.
Понятие числа e. Понятие экспоненты, натурального логарифма.
Формулы дифференцирования показательной функции.
IV. Закрепление изученного материала.
Разбор образцов примеров на нахождение производной показательной функции.
Решение упражнений из учебника.
V. Срезовая работа.
VI. Итог урока. Оценки.
VII. Домашнее задание.
Слайд 5I. Постановка цели.
Объявляется тема урока: «Производная показательной функции».
Сообщается, что сегодняшнем
уроке будут изучены формулы дифференцирования показательной функции. Для этого на I этапе урока учащиеся выполнят практическую исследовательскую работу на компьютере с помощью приложении Advanced Grapher. В конце урока будет проведена срезовая работа по новому материалу.
Слайд 6II. Актуализация знаний
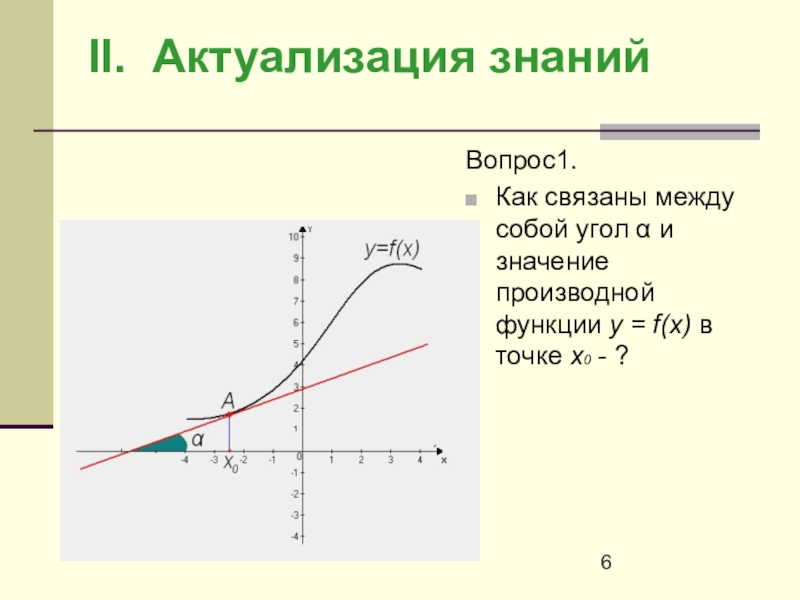
Вопрос1.
Как связаны между собой угол α и значение
производной функции у = f(х) в точке х0 - ?
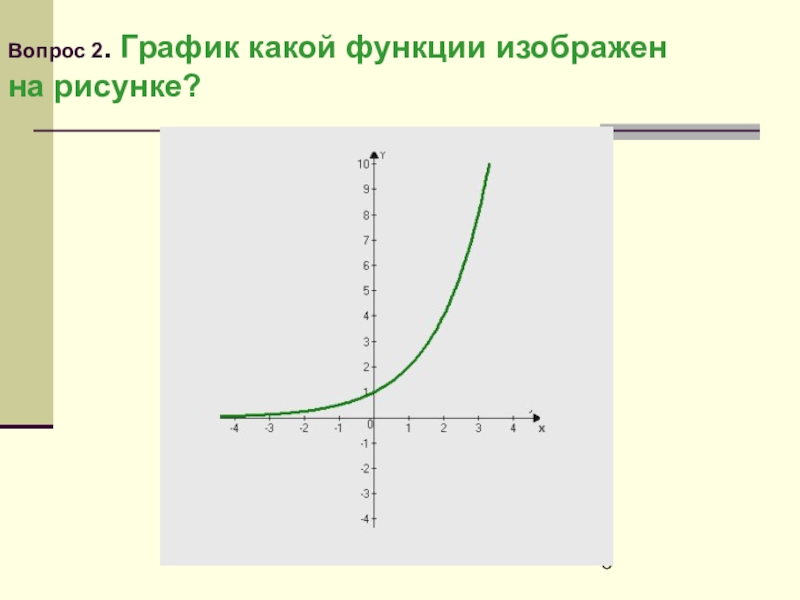
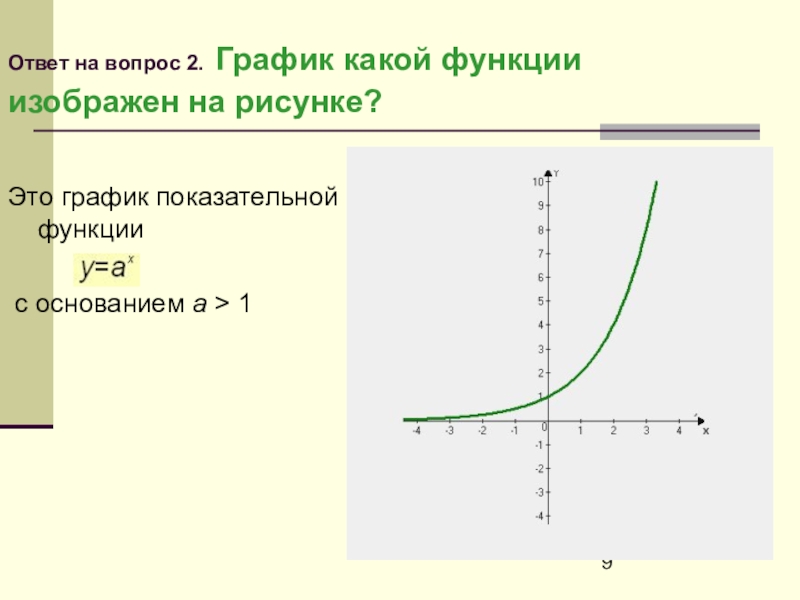
Слайд 9Ответ на вопрос 2. График какой функции изображен на рисунке?
Это график
показательной функции
с основанием a > 1
с основанием a > 1
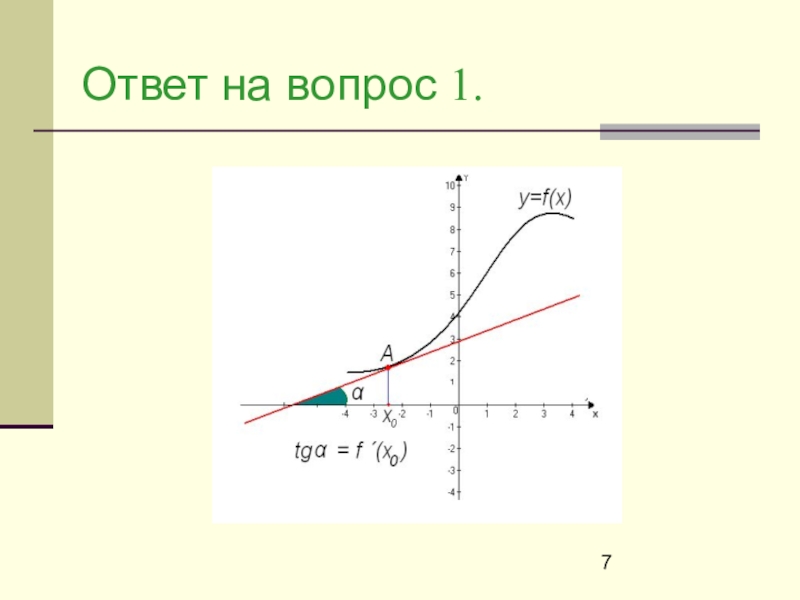
Слайд 11Ответ. Нужно построить касательную к графику функции
в точке х=0 и найти тангенс угла наклона касательной к положительному направлению оси OX.
Слайд 12III. Изучение нового материала
На сегодняшнем уроке вы выполните исследовательскую работу
на компьютере с помощью приложения Advanced Grapher.
Задание для исследовательской работы.
Среди функций
найти ту, для графика которой прямая у=х+1 является касательной в точке x0=0 ( путем последовательного построения их графиков)
Задание для исследовательской работы.
Среди функций
найти ту, для графика которой прямая у=х+1 является касательной в точке x0=0 ( путем последовательного построения их графиков)
Слайд 17Исследовательская практическая работа за компьютером
Примечание. На каждом компьютерном столе лежит
лист с инструкцией к выполнению работы.
Инструкция к выполнение работы:
Запустить программу Advanced Grapher.
1. Построить график функции у=х+1.
2. В той же системе координат построить
график функции , где а=1,5.
3. Сделать запись в таблице:
Инструкция к выполнение работы:
Запустить программу Advanced Grapher.
1. Построить график функции у=х+1.
2. В той же системе координат построить
график функции , где а=1,5.
3. Сделать запись в таблице:
Слайд 19
4. Проделать пункты 1, 2. и 3. этого алгоритма для a=
1,7; 1,9; 2,1; 2.3; 2.5; 2,7; 2,9; 3,1, наблюдая, как изменяется положение точек пересечения графиков.
5. Записать в рабочей тетради то значение а, при котором прямая y=x+1 имеет только одну общую точку графиком функции , т. е. является касательной к графику этой функции
6. Ответить на вопрос:
При каком а для функции выполняется условие: у´(о)= tg45=1 ?
5. Записать в рабочей тетради то значение а, при котором прямая y=x+1 имеет только одну общую точку графиком функции , т. е. является касательной к графику этой функции
6. Ответить на вопрос:
При каком а для функции выполняется условие: у´(о)= tg45=1 ?
Слайд 21Теорема
Примем без доказательства теорему:
Существует такое число больше 2 и меньше 3
(это число обозначают буквой е), что показательная функция в точке 0 имеет производную, равную 1, т.е. в этой точке касательная к графику функции составляет угол 45 градусов
Слайд 22В анализе доказано, что число e иррациональное. С помощью ЭВМ у
этого числа найдено более 2-х тысяч десятичных знаков после запятой.
е=2,718281828459045…
Показательную функцию называют экспоненциальной функцией.
График функции называют экспонентой
logе=lnх – натуральный логарифм.
Слайд 29VI. Итог урока.
Выясняется (поднятием рук), какие учащиеся получили оценку «3», «4»,
«5».
Учитель поощряет справившихся учащихся похвалой, одобрительным кивком,и т.д.
Заключительный вопрос:
Как вы поняли, что такое число е?
Учитель поощряет справившихся учащихся похвалой, одобрительным кивком,и т.д.
Заключительный вопрос:
Как вы поняли, что такое число е?
Слайд 31VII. Домашнее задание
п.41. Прочитать. Выучить формулы и формулировки теорем.
№№ 538-540(в, г)
Индивидуальные
задания.
Теоремы 1, 2 (с доказательством).
Теоремы 1, 2 (с доказательством).
Слайд 32Литература
АЛГЕБРА И НАЧАЛА АНАЛИЗА
Учебник для 10-11 классов средней школы
под редакцией
А. Н. Колмогорова
Москва Дрофа 2007
Москва Дрофа 2007