- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа для 10-11 классов.
Содержание
- 1. Презентация по алгебре и началам анализа для 10-11 классов.
- 2. Математика – одна из древнейших наук. За
- 3. Они внесли особый вклад в развитие математики!Л.В.
- 4. Периодические процессыВ природе и технике часто встречаются
- 5. Периодические функции Определение 1:Число T называют периодом
- 6. Теорема 1.Если T- период функции f, то
- 7. Следствие.Если Т-период функции f, то при любом
- 8. Определение 2:Функцию f называют периодической, если она
- 9. Определение 3:Наименьший положительный период функции называется основным
- 10. Теорема 2:Если Т- основной период функции f,
- 11. Примеры периодических функцийФункция y= [x]=x- {x}, где каждому числу x ставится в соответствие целая часть.
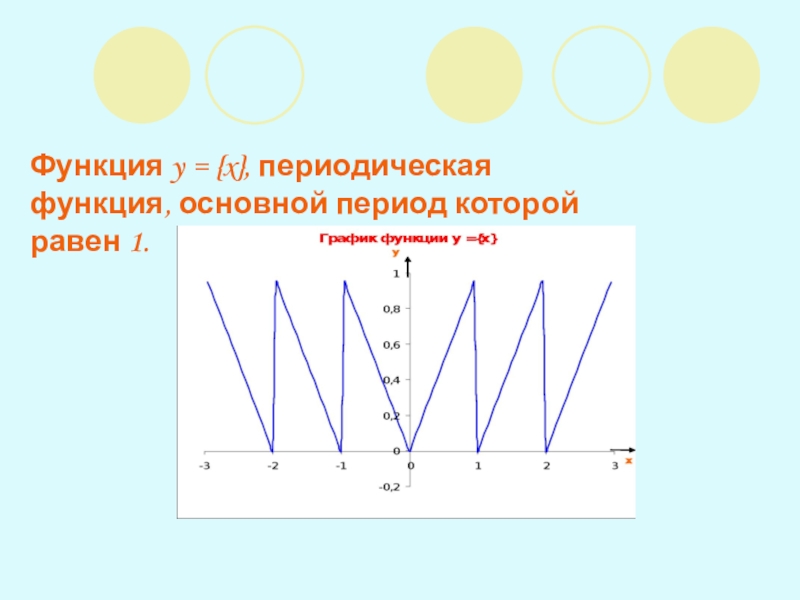
- 12. Функция y = {x}, периодическая функция, основной период которой равен 1.
- 13. Функции cos t и sin t –
- 14. Равенства (1), (2) доказывают, что -
Слайд 2Математика – одна из древнейших наук. За долгую историю своего существования
Чрезвычайно расширились связи математики с другими науками. Теперь она с успехом используется и в таких областях научного знания, о которых ещё недавно думали, что они не допускают внедрения математических методов. Такое мнение существовало о биологии, медицине, языкознании и некоторых отраслях общественных наук.
Возможности использовать математику для решения практических задач промышленности, сельского хозяйства и транспорта ныне представляются неограниченными.
Слайд 3Они внесли особый вклад в развитие математики!
Л.В. Канторович
Выдающийся советский математик, ныне
А.Н. Колмогоров
Герой Социалистического Труда, академик. Создал новую область математики -теорию информации.
А.Н. Крылов
Российский математик, академик Герой Социалистического Труда. Впервые в истории науки сформулировал один из принципов вычислительной культуры.
Слайд 4Периодические процессы
В природе и технике часто встречаются процессы, которые периодически повторяются
Например, если маятник делает одно полное колебание за Т секунд, то его отклонение от положения равновесия в моменты времени t, t+T, t+2T и т.д. будет одним и тем же.
Периодически с периодом в 1 год меняется расстояние Земли от Солнца.
С периодом в 1 лунный месяц меняются фазы Луны.
Периодически изменяющиеся величины описывают с помощью периодических функций.
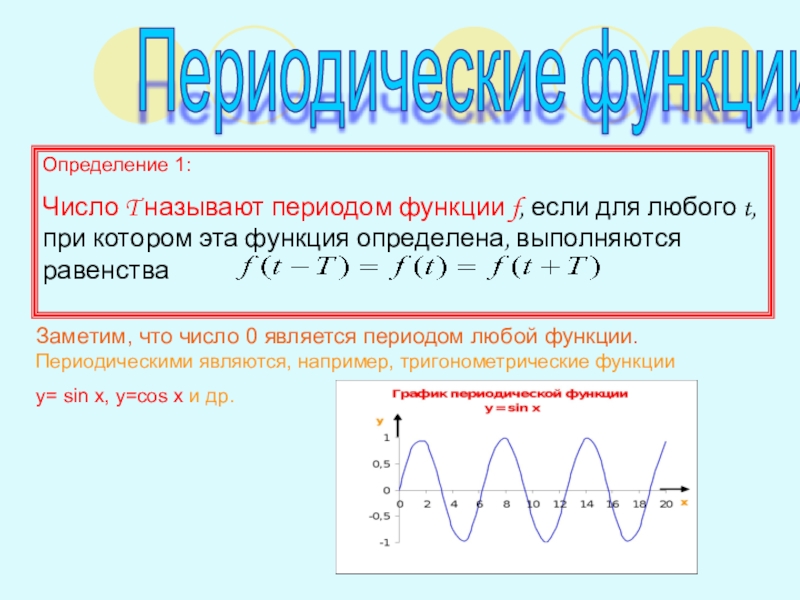
Слайд 5Периодические функции
Определение 1:
Число T называют периодом функции f, если для
Заметим, что число 0 является периодом любой функции. Периодическими являются, например, тригонометрические функции
y= sin x, y=cos x и др.
Слайд 6Теорема 1.
Если T- период функции f, то –T тоже является периодом
Доказательство.
Первое утверждение вытекает из того, что равенство
числа T и –Т входят равноправно. Второе же утверждение следует из того, что
и аналогично
Слайд 7Следствие.
Если Т-период функции f, то при любом целом значении n число
Доказательство.
Пусть n –натуральное число.
При n=1 истинность следствия вытекает из того, что T – период функции f.
Если kT –период этой функции, то по второму утверждению той же теоремы и kT+T=(k+1)T является ее периодом.
С помощью математической индукции убеждаемся в справедливости следствия для всех натуральных, а следовательно, и для всех целых значений n.
Слайд 8Определение 2:
Функцию f называют периодической, если она имеет хотя бы один
Если Т – положительный период функции f и известен график этой функции на каком-либо промежутке [a;a+T), то можно получить ее график на всей числовой оси с помощью параллельных переносов вдоль оси абсцисс на kT, где k Z. Обычно выбирают a=0 или
Если функция f постоянна, то любое число является ее периодом. Можно доказать, что если функция f отлична от постоянной, непрерывна и периодична, то среди ее положительных периодов есть наименьший.
Слайд 9Определение 3:
Наименьший положительный период функции называется основным периодом этой функции.
Пример 1.
Докажем,
Решение. От прибавления к x целого числа дробная часть x не меняется. Поэтому любое отличное от нуля целое число является периодом функции y={x}. Наименьшим из положительных целых чисел является 1.
Докажем, что число 1 – основной период функции {x}. Для этого достаточно показать, что ни одно положительное число T меньшее, чем 1, не может быть периодом функции y={x}. Но при x=0 имеем {x}=0, а {x+T} = {T} = T 0 (поскольку 0 Значит, равенство {x}={x+T} не выполняется при x=0, и поэтому T не является периодом функции {x}. Это и означает, что основной период функции y={x} равен 1.
Слайд 10Теорема 2:
Если Т- основной период функции f, то все остальные периоды
Доказательство. В силу теоремы 1 достаточно провести доказательство для положительных периодов функции f. Если Т1 – такой период, то он не может быть меньше Т, так как Т-наименьший из положительных периодов функции f. Но если Т1 Т, то найдется такое натуральное число n, что nT T1<(n+1)T. Из теоремы 1 и ее следствия вытекает, что –nT, а потому и Т1-nT – период функции f. Но 0 Т1 – nT<Т, а из сказанного выше следует, что период Т1-nT не может быть положительным и меньшим, чем Т. Значит, Т1 – nT = 0, т.е. Т1=nT.
Слайд 11Примеры периодических функций
Функция y= [x]=x- {x}, где каждому числу x ставится
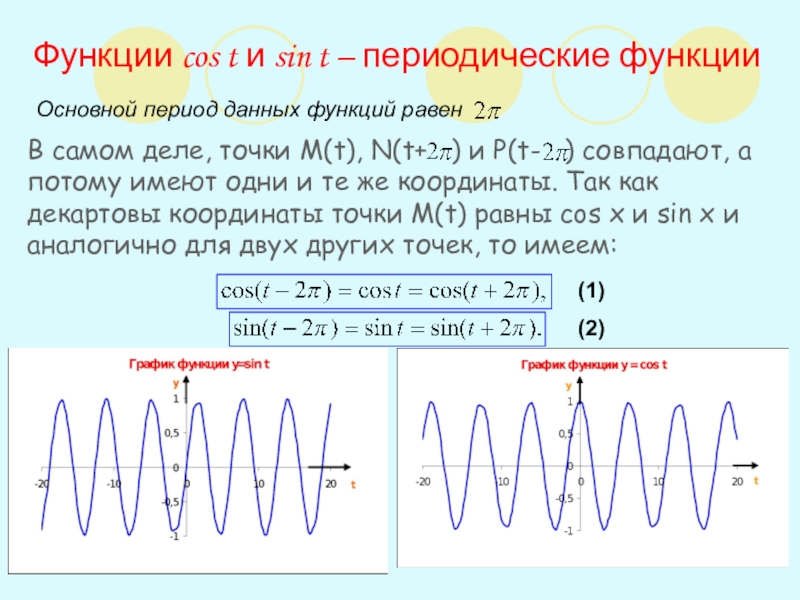
Слайд 13Функции cos t и sin t – периодические функции
Основной период данных
В самом деле, точки М(t), N(t+ ) и P(t- ) совпадают, а потому имеют одни и те же координаты. Так как декартовы координаты точки M(t) равны cos x и sin x и аналогично для двух других точек, то имеем:
(1)
(2)
Слайд 14Равенства (1), (2) доказывают, что - один из положительных периодов
В самом деле, если бы Т, где 0









![Презентация по алгебре и началам анализа для 10-11 классов. Примеры периодических функцийФункция y= [x]=x- {x}, где каждому числу x ставится в соответствие целая часть. Примеры периодических функцийФункция y= [x]=x- {x}, где каждому числу x ставится в соответствие целая часть.](/img/thumbs/9028ada0644e37d5f1e57bfb6d2a1bcb-800x.jpg)