Автор: Живаева Любовь Николаевна,
учитель математики МБОУООШ с.Колдаис
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре для 9 класса Решение неравенств второй степени с одной переменной
Содержание
- 1. Презентация по алгебре для 9 класса Решение неравенств второй степени с одной переменной
- 2. «Доводы, до которых человек додумывается сам, обычно
- 3. Цель урока. Сформировать знания о
- 4. Задачи урока:Образовательные: 1.Организовать деятельность учащихся:
- 5. ax2 + bx + c = 0
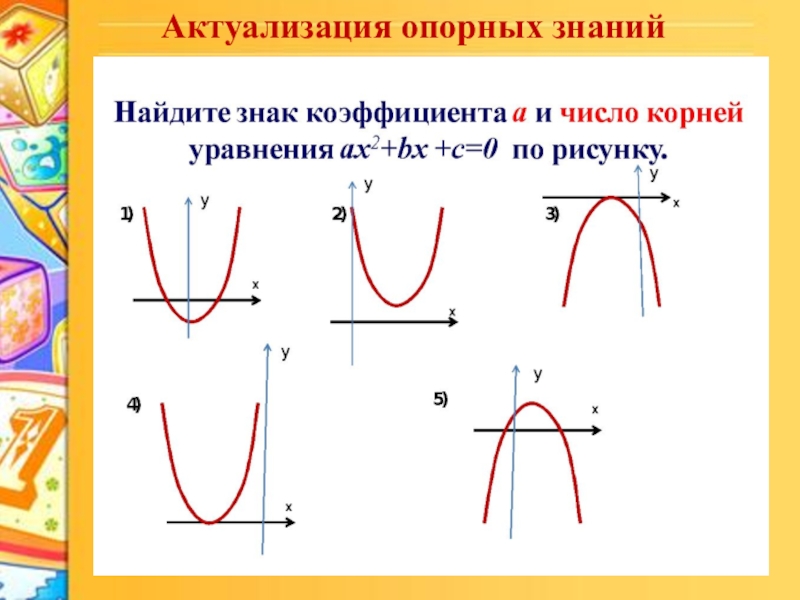
- 6. Актуализация опорных знаний
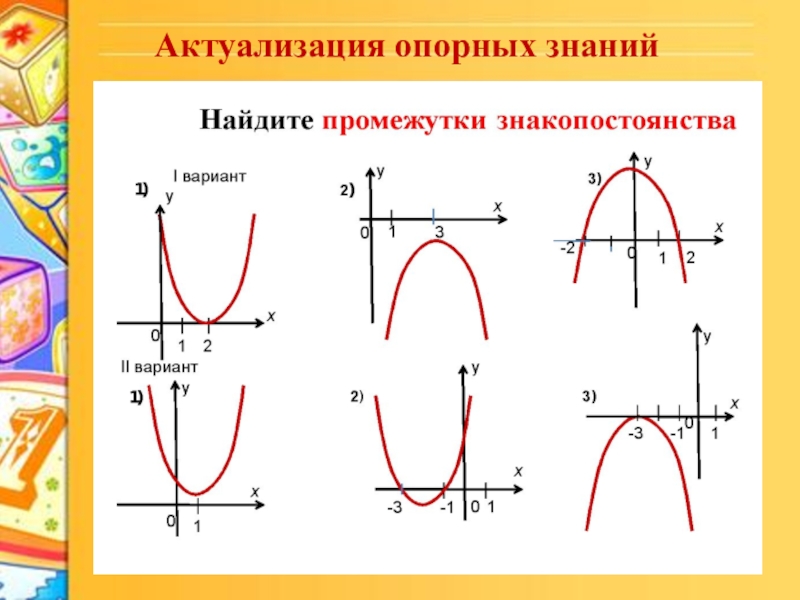
- 7. Актуализация опорных знаний
- 8. Проверь себя:у > 0, х € (-
- 9. Неравенства второй степени с одной переменнойax2 +
- 10. Определение неравенства второй степени с одной переменнойНеравенства
- 11. Решение неравенств второй степени с одной переменнойРешение
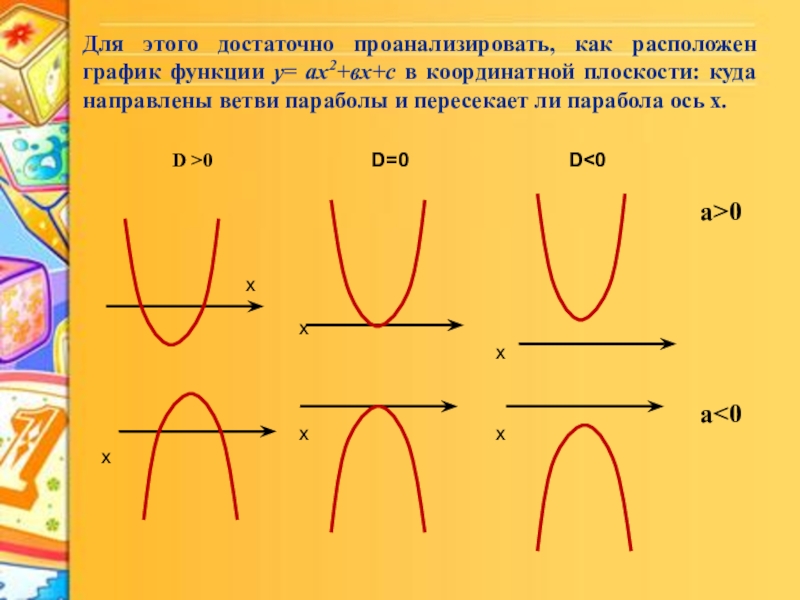
- 12. Для этого достаточно проанализировать, как расположен график
- 13. ххххххх2хх
- 14. Решить неравенство 5x2+9x-2>0Введем функцию у =5x2+9x-2
- 15. Решить неравенство -5x2+9x+2>0Введем функцию у
- 16. Алгоритм решения неравенств второй степени с одной
- 17. Работа в парах
- 18. -33353.....Проверь себя:
- 19. Блез Паскаль (19 июня 1623—19 августа 1662) французский математик, физик, литератор и философ.
- 20. Итог урока.Какие новые знания получили на уроке?Сформулируйте
- 21. Рефлексия урока: На уроке я был:
- 22. Домашнее задание.п.14. Выучить определение и алгоритм
Слайд 1Муниципальное бюджетное общеобразовательное учреждение
Основная общеобразовательная школа с.Колдаис
Тема урока:
«Решение неравенств
Слайд 2«Доводы, до которых человек додумывается сам,
обычно убеждают его больше, нежели
которые пришли в голову другим» .
Блез Паскаль
Слайд 3Цель урока.
Сформировать знания о неравенствах второй степени
Слайд 4Задачи урока:
Образовательные:
1.Организовать деятельность учащихся:
- по формированию понятия неравенства второй степени с одной переменной;
- по выведению алгоритма решения неравенств второй степени с одной переменной на основе свойств квадратичной функции.
2. Обеспечить закрепление понятия неравенства второй степени с одной переменной, умений решать неравенства второй степени по алгоритму с помощью схематического графика квадратичной функции.
Развивающие:
- развивать умение выделять главное, анализировать, обобщать;
- развивать логическое мышление, навыки самопроверки, самоконтроля; - развивать культуру речи учащихся: умение вести диалог, грамотно использовать математические термины, аргументированно высказывать точку зрения.
Воспитательные:
- воспитывать прилежание, трудолюбие, познавательный интерес к предмету;
- формировать навыки общения, умения работать в коллективе, уважительное отношение к мнению каждого.
Слайд 5ax2 + bx + c = 0
ax2 + bx +
у = ax2 + bx + c
где х – переменная, а, b и с – некоторые числа,
причем а = 0
Актуализация опорных знаний
Слайд 8Проверь себя:
у > 0, х € (- ∞; + ∞);
2) у > 0, х € (- ∞; - 3) U (- 1; + ∞);
у < 0, х € (- 3; -1);
3) у < 0, х € (- ∞; - 3) U (- 3; + ∞).
Слайд 9Неравенства второй степени с одной переменной
ax2 + bx + c >
ax2 + bx + c < 0
ax2 + bx + c ≥ 0
ax2 + bx + c ≤ 0
Изучение нового материала
Слайд 10Определение неравенства второй степени с одной переменной
Неравенства вида
ax2
(ax2 + bx + c ≥ 0; ax2 + bx + c ≤ 0)
где x – переменная, a, b и c – некоторые числа и a ≠ 0, называют неравенствами второй степени с одной переменной.
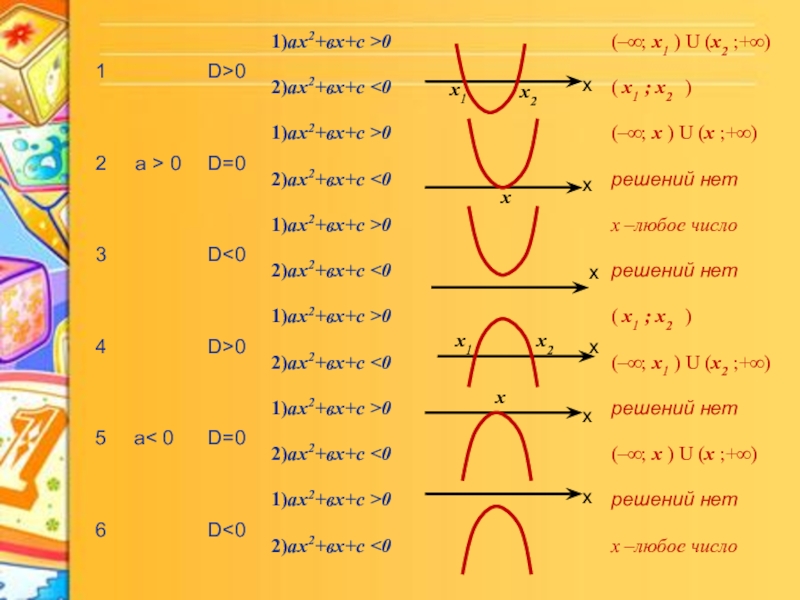
Слайд 11Решение неравенств второй степени с одной переменной
Решение неравенства
ax2 + bx
(ax2 + bx + c ≥ 0 или ax2 + bx + c ≤ 0)
можно рассматривать как нахождение промежутков знакопостоянства (промежутков в которых функция y = ax2 + bx + c принимает положительные или отрицательные значения).
Слайд 12Для этого достаточно проанализировать, как расположен график функции y= аx2+вx+с в
х
Слайд 14Решить неравенство
5x2+9x-2>0
Введем функцию
у =5x2+9x-2
а>0, ветви параболы
направлены
Найдем нули функции (у=0) у =5x2+9x-2
х1 = 1/5;х 2 = -2
Отметим точки
х1 = 1/5;х 2 = -2 на оси Ох
-2
1/5
Изобразим схематически график функции
y= 5x2+9x-2
y= 5x2+9x-2
Найдем промежутки, в которых у>0 (имеет знак +)
Заштрихуем эти промежутки
у>0 на промежутках (–∞;-2) U (1/5;+∞)
Ответ: (–∞;-2) U (1/5;+∞)
5x2+9x-2≥0
Ответ: (–∞;-2] U [1/5;+∞)
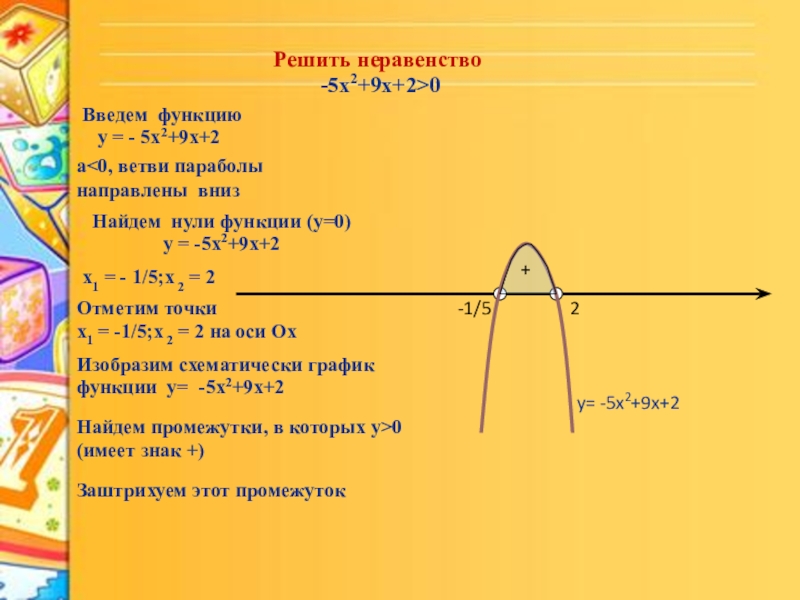
Слайд 15 Решить неравенство
-5x2+9x+2>0
Введем функцию
у = - 5x2+9x+2
а<0, ветви параболы
направлены вниз
Найдем нули функции (у=0)
у = -5x2+9x+2
х1 = - 1/5;х 2 = 2
Отметим точки
х1 = -1/5;х 2 = 2 на оси Ох
-1/5
2
Изобразим схематически график функции y= -5x2+9x+2
y= -5x2+9x+2
Найдем промежутки, в которых у>0 (имеет знак +)
+
Заштрихуем этот промежуток
у>0 на промежутке (–1/5;-2)
Ответ: (–1/5;2)
-5x2+9x+2≥0
Ответ: [–1/5;2]
Слайд 16Алгоритм
решения неравенств второй степени с одной переменной
Ввести квадратичную функцию.
Определить
Найти нули функции, если они есть ( значение D и корни уравнения, если они есть).
Изобразить эскиз графика соответствующей квадратичной функции, используя полученные нули функции (если они есть), с учетом направления ветвей.
Выбрать промежутки, в которых функция принимает значения, соответствующие данному квадратному неравенству. Записать ответ.
Слайд 19Блез Паскаль
(19 июня 1623—19 августа 1662)
французский математик, физик,
литератор и философ.
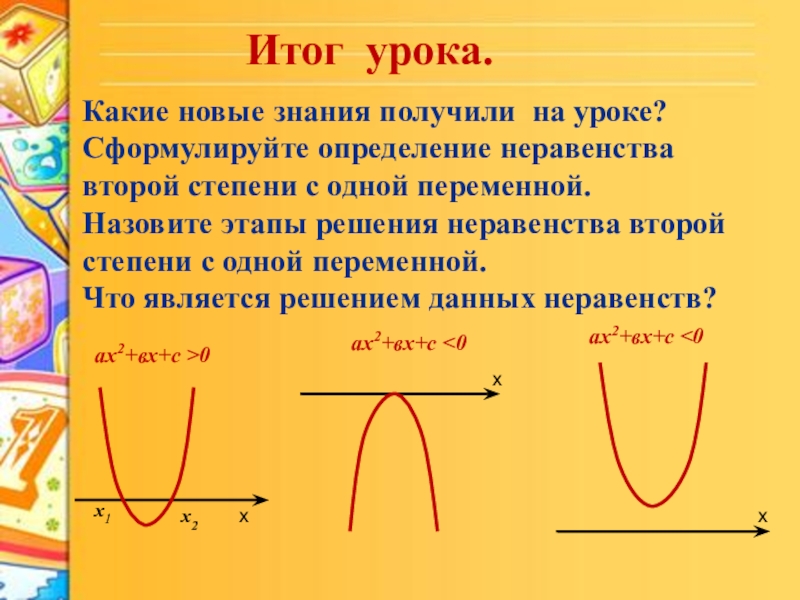
Слайд 20Итог урока.
Какие новые знания получили на уроке?
Сформулируйте определение неравенства второй степени
Назовите этапы решения неравенства второй степени с одной переменной.
Что является решением данных неравенств?
х
х
х
аx2+вx+с >0
аx2+вx+с <0
аx2+вx+с <0
х1
х2
Слайд 21Рефлексия урока:
На уроке я был: активен / пассивен.
За урок я: не устал / устал.
Новый материал: понял полностью / понял частично / не понял.
Самооценка знаний _____.
Слайд 22 Домашнее задание.
п.14. Выучить определение и алгоритм решения неравенств второй степени
1 уровень – N3059;
2 уровень – N 312 a,б,в.
Подготовить по одному устному заданию по теме урока.