- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре для 7-го класса на тему Вынесение общего множителя за скобки
Содержание
- 1. Презентация по алгебре для 7-го класса на тему Вынесение общего множителя за скобки
- 2. Среди ученых известна шутка: «Неважно,
- 3. Проверьте, правильно ли выполнено задание Сегодня нам
- 4. Что? Под разложением многочлена на
- 5. Зачем? О пользе разложения на
- 6. Зачем? Разложение на множители часто упрощает
- 7. Как? Как разлагать многочлен на множители?
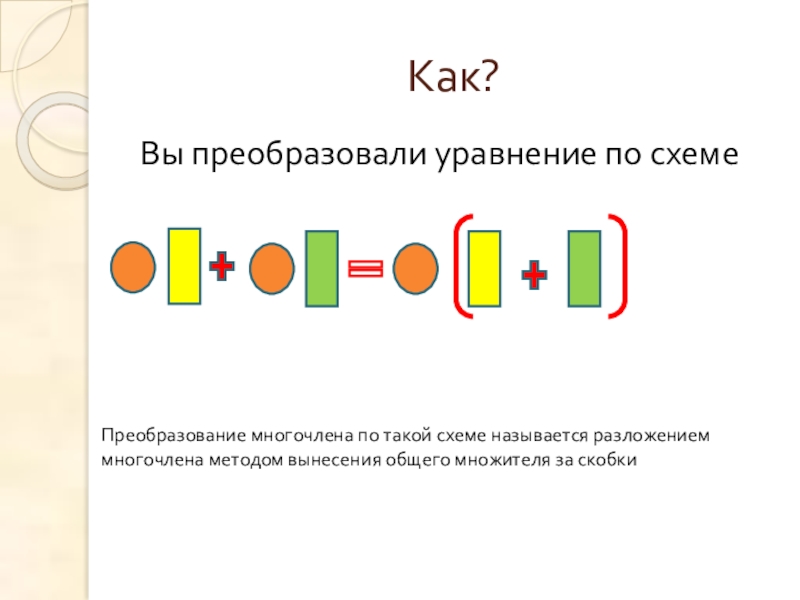
- 8. Как?Вы преобразовали уравнение по схемеПреобразование многочлена по
- 9. Метод группировки слагаемыхВычислите рациональным путем:121*13+12*121+13*179+12*179
- 10. Упражнение 1. Разложите многочлены на множители,
- 11. Упражнение 2. 12+18у 4а2-4вс -3ав+16в
- 12. Ответьте на вопросыКакая арифметическая операция используется, когда
- 13. Упражнение 3.Закончите разложение на множители и объясните
- 14. Упражнение 4.Разложите многочлены на множители двумя способами:nх
- 15. Метод группировкиВсе слагаемые многочлена объединяем в группы:
- 16. Задание 1. 1) Заполните пропуски в разложении
- 17. Задание 2. Вычислите рациональным способом: 48,8*3,8 -48,8*2,89,2*34 +9,2*16(0,823)*2+0,823*5,43 – 5,253*0,823(1,67+0,33)*1,67
- 18. Задание 3. Заполните пропуски:3а2в-6ав2=ав(… - …)=3ав( …
- 19. Задание 4. В выражении 9х+3в – 6а
- 20. Задание 5. Вынесите за скобки все возможные
- 21. Задание 6. Разложите на множители методом вынесения
- 22. Задание 7Вставьте пропущенные выраженияm(x +y) – x
- 23. Задание 8. Проверьте равенство 54,4*43,2 – 25,6*18,2 -54,4*18,2 +25,6*43,2= =2000
- 24. Задание 9. Вычислите рациональным способом: 93*52 –
- 25. Задание 10. Разложите на множители методом группировки:
- 26. Задание 11. Впишите пропущенные одночлены: 6а3 –
- 27. Задание 12. Решите уравнения:а) 6у+5 -2(6у+5)=0
- 28. Задание 13. При разложении многочленов на множители
Среди ученых известна шутка: «Неважно, что происходит, а важно, как на это посмотреть» Полезно иногда посмотреть на старые вещи по-новому. Это-то я и предлагаю вам сделать вместе со мной.
Слайд 2 Среди ученых известна шутка: «Неважно, что происходит, а важно,
как на это посмотреть»
Полезно иногда посмотреть на старые вещи по-новому. Это-то я и предлагаю вам сделать вместе со мной.
Полезно иногда посмотреть на старые вещи по-новому. Это-то я и предлагаю вам сделать вместе со мной.
Слайд 3Проверьте, правильно ли выполнено задание
Сегодня нам предстоит решать обратную задачу
с(2с-3)=2с2
– 3с
(х-2)(х+3)= х2 +х - 6
(а+в)(х+у)= ах+ау+вх+ву
(а-в)(а+в)=а2 – в2
(х-2)(х+3)= х2 +х - 6
(а+в)(х+у)= ах+ау+вх+ву
(а-в)(а+в)=а2 – в2
Слайд 4Что?
Под разложением многочлена на множители будем понимать представление многочлена
в виде произведения многочленов, каждый из которых зависит хотя бы от одной переменной.
Слайд 5Зачем?
О пользе разложения на множители вы знаете уже давно.
Убедитесь в этом еще раз – вычислите значение выражения рациональным способом:
19*83+17*19
26-11*26
ав+ас-аd, при а= 47, в= 54, с= 36, d = 40
ху-хz, при х=17, у=29, z= 19
19*83+17*19
26-11*26
ав+ас-аd, при а= 47, в= 54, с= 36, d = 40
ху-хz, при х=17, у=29, z= 19
Слайд 6Зачем?
Разложение на множители часто упрощает работу. Стоит, например, разложить на
множители левую часть уравнения х2 – 2х – 24 =0 и решение уравнения будет легко найдено:
х2 – 2х – 24=(х-6)(х+4)
Уравнение (х-6)(х+4)=0 решается так:
х – 6 =0 или х+4 = 0
Закончите решение…
х2 – 2х – 24=(х-6)(х+4)
Уравнение (х-6)(х+4)=0 решается так:
х – 6 =0 или х+4 = 0
Закончите решение…
Слайд 7Как?
Как разлагать многочлен на множители? Именно этому мы и будем
учиться
Задание 1.
Решите уравнение, разлагая многочлен на множители:
7х2 – 2х=0
Задание 1.
Решите уравнение, разлагая многочлен на множители:
7х2 – 2х=0
Слайд 8Как?
Вы преобразовали уравнение по схеме
Преобразование многочлена по такой схеме называется разложением
многочлена методом вынесения общего множителя за скобки
Слайд 10Упражнение 1.
Разложите многочлены на множители, если это возможно, и
сделайте проверку.
0,5+0,5в
0,7х2-0,2х2у
6,3*0,4 -3,4*6,3
(а+в)х+(а+в)у
а2-2в
0,5+0,5в
0,7х2-0,2х2у
6,3*0,4 -3,4*6,3
(а+в)х+(а+в)у
а2-2в
1,2а2-1,2а3в2=1,2а2*1-1,2а2*ав2=1,2а2(1-ав2)
5х(а-2в)+2(2в-а)=5х(а-2в)-2(а-2в)=(а-2в)(5х-2)
Подсказка:
Слайд 11Упражнение 2.
12+18у
4а2-4вс
-3ав+16в
10ав -20ав
х4 +2х2
2*33+35
ас+с+с2
6х2(х-р)2-(х-р)2
3х+6х2
-8у3-24у2
27*33 – 9*35
9а2к6 - 18 а4к4+24а6к2
а(х-у)+в(х-у)
(а-в) + 2х(в-а)
а2(х -2) +в(2 – х)
х(у – 3)+2(3-у)
Вынесите общий множитель за скобку и сделайте проверку:
Слайд 12Ответьте на вопросы
Какая арифметическая операция используется, когда находится общий числовой множитель?
Какая
алгебраическая операция используется, когда находится общий множитель, являющийся переменной или степенью переменной?
Слайд 13Упражнение 3.
Закончите разложение на множители и объясните каждый шаг:
ас +вс +
ап+вп =ас + вс + ап + вп =
=(ас + вс) + (ап +вп) = с(а + в) + п(а +в) =
=(с +п)(а+в)
ас + вс + ап +вп = ас+вс +ап + вп= (…) + (…)=…
=(ас + вс) + (ап +вп) = с(а + в) + п(а +в) =
=(с +п)(а+в)
ас + вс + ап +вп = ас+вс +ап + вп= (…) + (…)=…
Слайд 14Упражнение 4.
Разложите многочлены на множители двумя способами:
nх +nу + bх +bу
а3+2а2+2а+4
Опишите последовательность действий при разложении многочлена на множители методом группировки.
Слайд 15Метод группировки
Все слагаемые многочлена объединяем в группы: каждая группа должна содержать
свой общий множитель.
Вынося его за скобки, преобразуем группу в произведение.
При подходящем выборе групп все полученные произведения будут иметь общий множитель.
Вынося его за скобки, получаем разложение многочлена на множители
Вынося его за скобки, преобразуем группу в произведение.
При подходящем выборе групп все полученные произведения будут иметь общий множитель.
Вынося его за скобки, получаем разложение многочлена на множители
Слайд 16Задание 1.
1) Заполните пропуски в разложении одночлена на множители:
72
авх2=8а*…=12вх*…=3*…
2) Представьте выражения в виде возможно большего числа множителей:
а) 40ав2
б)121а2вху
в) 180 р2q2
2) Представьте выражения в виде возможно большего числа множителей:
а) 40ав2
б)121а2вху
в) 180 р2q2
Слайд 17Задание 2.
Вычислите рациональным способом:
48,8*3,8 -48,8*2,8
9,2*34 +9,2*16
(0,823)*2+0,823*5,43 – 5,253*0,823
(1,67+0,33)*1,67
Слайд 19Задание 4.
В выражении 9х+3в – 6а вынесите за скобки 3
В
выражении 11а – 3 – 9 б вынесите за скобки 3
В выражении 0,5 у + 0,25 а – 0,75 вынесите за скобки 0,25
В выражении 0,5 у + 0,25 а – 0,75 вынесите за скобки 0,25
Слайд 20Задание 5.
Вынесите за скобки все возможные множители:
7а2в2+14а3в – 28 ав3
х3
+ 3 х2 + х
3ах(5х2 – 15 у2)-6ау(6у2 – 2х2)
3ах(5х2 – 15 у2)-6ау(6у2 – 2х2)
Слайд 21Задание 6.
Разложите на множители методом вынесения за скобки общего множителя
а)
8а + 8в б) 3х – 3 в) ах + ау г) х2 – х д) 12а – 18 в е ) 18а2 – 9 а3 + 3а4
а) 48х2у – 36 ху б) 85 ав – 170а в) mx – nx + px г) 8авх – 6 асу – 10 ак д) 0,3с5р3 + 0,7 с4р4 е) 15 а2у4 +9ау2 + 27 ау
а) а(х+у) +в(х + у) б) а(х-у) – в(х-у) в) t(2x – 3y) – 5(-2x +3y) г)2x(3p-q) – (3p – q)
а) 48х2у – 36 ху б) 85 ав – 170а в) mx – nx + px г) 8авх – 6 асу – 10 ак д) 0,3с5р3 + 0,7 с4р4 е) 15 а2у4 +9ау2 + 27 ау
а) а(х+у) +в(х + у) б) а(х-у) – в(х-у) в) t(2x – 3y) – 5(-2x +3y) г)2x(3p-q) – (3p – q)
Слайд 22Задание 7
Вставьте пропущенные выражения
m(x +y) – x – y = m(x
+y) – (… + ….)= =(x + y)(… - 1)
ab – a – b +1 = (ab – a) – (b – 1) =
=a(… -…) – (b-1) =…
40 x2 – 2 p +5 x – 16 px = (40 x2 – 16 px) + +(5x – 2p)= …(5x -2p)+(5x – 2p) =
=(…) (… +1)
21 a2-35b – 6 a2x3+10bx3=…(2x3-7) –
- …(….) = (2x3 -7)(…)
ab – a – b +1 = (ab – a) – (b – 1) =
=a(… -…) – (b-1) =…
40 x2 – 2 p +5 x – 16 px = (40 x2 – 16 px) + +(5x – 2p)= …(5x -2p)+(5x – 2p) =
=(…) (… +1)
21 a2-35b – 6 a2x3+10bx3=…(2x3-7) –
- …(….) = (2x3 -7)(…)
Слайд 24Задание 9.
Вычислите рациональным способом:
93*52 – 38*43 + 93*38 –
43*52
12,7*3,4 +8,2*1,4 – 1,4*12,7 – 3,4*8,2
(78,5)2+21,5*93,4 – 21,5*14,9
12,7*3,4 +8,2*1,4 – 1,4*12,7 – 3,4*8,2
(78,5)2+21,5*93,4 – 21,5*14,9
Слайд 25Задание 10.
Разложите на множители методом группировки:
а) ах + ау
+ 10х + 10у
б) а2 – ав – 8а +8в
в) а2n – anx + x2 – ax
г)5a3c + 10a2 - 6bc – 3abc2
а) аn2 + cn2 – ap + ap2 – cp + cp2
б) 3a3 + 5abc + 6ab2 – a3c – 15a2b – 2b2c
в) х5 – х4 +х3-х2+х – 1
б) а2 – ав – 8а +8в
в) а2n – anx + x2 – ax
г)5a3c + 10a2 - 6bc – 3abc2
а) аn2 + cn2 – ap + ap2 – cp + cp2
б) 3a3 + 5abc + 6ab2 – a3c – 15a2b – 2b2c
в) х5 – х4 +х3-х2+х – 1
Слайд 26Задание 11.
Впишите пропущенные одночлены:
6а3 – 15а2b -14 ab +
…=
=(2a – 5b)(… - ….)
12x3 - … + 42 x2y – 35 y3=
=(… - ….)(6x2 – 5 y2)
24 a4 – 18 a3 – 4 ab + … =
=(…. - ….)(… - ….)
=(2a – 5b)(… - ….)
12x3 - … + 42 x2y – 35 y3=
=(… - ….)(6x2 – 5 y2)
24 a4 – 18 a3 – 4 ab + … =
=(…. - ….)(… - ….)
Слайд 27Задание 12.
Решите уравнения:
а) 6у+5 -2(6у+5)=0
б) х(х-2) +7(2-х)=0
в) (3х-2)(х+4)-3(х+5)(х-1)=0
г) у2 + 8у – 4у – 32=0
Слайд 28Задание 13.
При разложении многочленов на множители получены следующие результаты:
n(3n
-4)2+(3n-4)3=4(3n-4)2(n-1)
14a2c + 25 b2d - 10abd – 35 abc=
=(2a -5b)(7ac – 5bd)
Проверьте правильность разложений двумя способами
14a2c + 25 b2d - 10abd – 35 abc=
=(2a -5b)(7ac – 5bd)
Проверьте правильность разложений двумя способами