- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Арифметическая и геометрическая прогрессии
Содержание
- 1. Презентация по алгебре Арифметическая и геометрическая прогрессии
- 2. Цель урока: обобщение тем «Арифметическая прогрессия» и
- 3. Эпиграф:
- 4. Историческая справка.В XVIII в в английских и
- 5. Эпизод из жизни Карла Гаусса.
- 6. Легенда о создании шахмат. Индийский царь Шерам
- 7. Слайд 7
- 8. 1) 2; 5; 8; 11;14; 17;… 2)
- 9. 3) Дано: (а n ) арифметическая
- 10. 4) Дано: (b n ) геометрическая прогрессия
- 11. 1)Дано: (а n ), а1 = –
- 12. Ответы: 1)
- 13. Выполните задания. В восточных странах Китае, Корее,
- 14. Ответ: ХАСИ
- 15. Фигуры составлены из квадратов,
- 16. 3.Вычислите сумму: 502 – 492 + 482
- 17. Слайд 17
- 18. Слайд 18
- 19. Задания из сборника предназначенного для подготовки к
- 20. Ответы:6.1 (20,4) 6.2. (является), 6.5. (6;8,2;10’4;12’6;14’8;17.), 6.8. (b1=34 или b1= –34).
- 21. Итог урока.Сегодня на уроке мы повторили определения
- 22. Литература:1.Глейзер Г.И.История математики в школе.-М.,Просвещение,1992г.2.МакарычевЮ.Н .и др.Алгебра
Слайд 1Тема урока:
Арифметическая и геометрическая прогрессии
Подготовила :учитель
математики и информатики,
Калымова
Слайд 2Цель урока: обобщение тем «Арифметическая прогрессия» и «Геометрическая прогрессия».
Задачи урока:
--
-- проконтролировать и развивать умения и навыки;
-- развивать познавательный интерес учащихся, учить их видеть связь между математикой и окружающей жизнью.
Слайд 3 Эпиграф:
« Что значит владение
Это есть умение решать задачи,
причем не только стандартного вида, но и
требующие известной независимости мышления,
здравого смысла, оригинальности,
изобретательности.
Д. Пойа.
Слайд 4
Историческая справка.
В XVIII в в английских и французских .учебниках появились обозначения
Некоторые формулы, относящиеся к прогрессиям , были известны китайским и индийским ученым. Например Ариабхатта (Vв.) знал формулы для общего члена и суммы арифметической прогрессии.
Слово прогрессия ( лат.progressio) означает «движение вперед»( как и слово «прогресс»), встречается впервые у римского автора Боэция.
В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания как их решать.
В древнеегипетском папирусе Ахмеса ( около 2000 лет до н.э) приводится такая задача:
«Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя ,полученного каждым человеком и его соседом , равнялось 1/8 меры»
А в одном из древнегреческих папирусов приводится следующая задача:
«Имеется 7 домов, в каждом доме по 7 кошек, каждая кошка съедает по 7 мышей , каждая мышь съедает 7 колосьев, каждый из которых, если посеять зерно, дает 7 мер зерна. Нужно посчитать сумму мер зерна».
Слайд 5Эпизод из жизни Карла Гаусса.
Однажды на уроке,
пока он будет заниматься с учениками третьего класса,
учитель велел сложить все числа от 1 до 100, надеясь,
что это займет много времени.
Но маленький Гаусс сразу сообразил,
что 1+100=101, 2+99=101 и т.д.
И таких чисел будет 50. Осталось 101 умножить на 50.
это мальчик сделал в уме.
Едва учитель закончил чтение условия,
он предъявил ответ, записанный на грифельной доске.
Изумленный учитель понял, что это самый способный ученик в его практике. В дальнейшем Гаусс сделал много замечательных открытий. Его даже назвали «царем математики».
Слайд 6
Легенда о создании шахмат. Индийский царь Шерам позвал к себе изобретателя
«Чтобы разместить это зерно в амбаре, то его размеры будут: высота 4 м, ширина 10 м,
длина будет 30 000 000 км – вдвое больше, чем расстояние от Земли до Солнца. А чтобы его получить,
то надо засеять пшеницей площадь всей Земли, считая моря, океаны, горы, пустыни, Арктику с Антарктикой,
то лет за пять царь смог бы рассчитаться с просителем»
Слайд 7 Опрос теоретического материала
Что называется последовательностью?
Какие виды последовательностей вы знаете?
Какая последовательность называется арифметической прогрессией?
Назовите формулу п +1 –го члена арифметической прогрессии.
(аn+1 = an + d )
5.Назовите формулу n –го члена арифметической прогрессии.
(an = a1 + d* (n – 1)
6.Какая прогрессия называется геометрической?
7.Назовите формулу п +1 –го члена геометрической прогрессии.
(bn+1 = bп *g)
8. Назовите формулу n –го члена геометрической прогрессии.
( bп = b 1 * g n-1 )
9.Назовите формулу суммы n –первых членов арифметической прогрессии
10. Назовите формулу суммы n –первых членов геометрической прогрессии
11. Назовите формулу суммы n –первых членов геометрической прогрессии
Слайд 81) 2; 5; 8; 11;14; 17;…
2) 3; 9; 27; 81;
3) 1; 6; 11; 20; 25;…
4) –4; –8; –16; –32; …
5) 5; 25; 35; 45; 55;…
6) –2; –4; – 6; – 8; …
арифметическая прогрессия d = 3
арифметическая прогрессия d = – 2
геометрическая прогрессия q = 3
последовательность чисел
геометрическая прогрессия q = 2
последовательность чисел
Слайд 93) Дано: (а n ) арифметическая прогрессия
а4 =
Найти: а1 .
Решение: используя формулу а n= а 1+ ( n – 1) d
а4 = а1 +3 d ; а1= а4 – 3 d =11 – 3 . 2 = 5
Ответ: 5.
Устный счет
Слайд 104) Дано: (b n ) геометрическая прогрессия
b4= 40 q
Найти: b1.
Решение: используя формулу b n = b1 q n-1
b4 =b1q3 ; b1 = b4 : q3 =40:23 =40 :8=5
Ответ: 5.
Слайд 11
1)Дано: (а n ), а1 = – 3, а2 = 4.
2)Дано: (b n ) , b 12 = – 32, b 13 = – 16.Найти: q – ?
3)Дано: (а n ), а21 = – 44, а22 = – 42. Найти: d - ?
4)Дано: (а n ), а1 = 28, а21 = 4. Найти: d - ?
5) Дано: (b n ) , , q = 2. Найти: b5 – ?
Работа в парах
Слайд 13
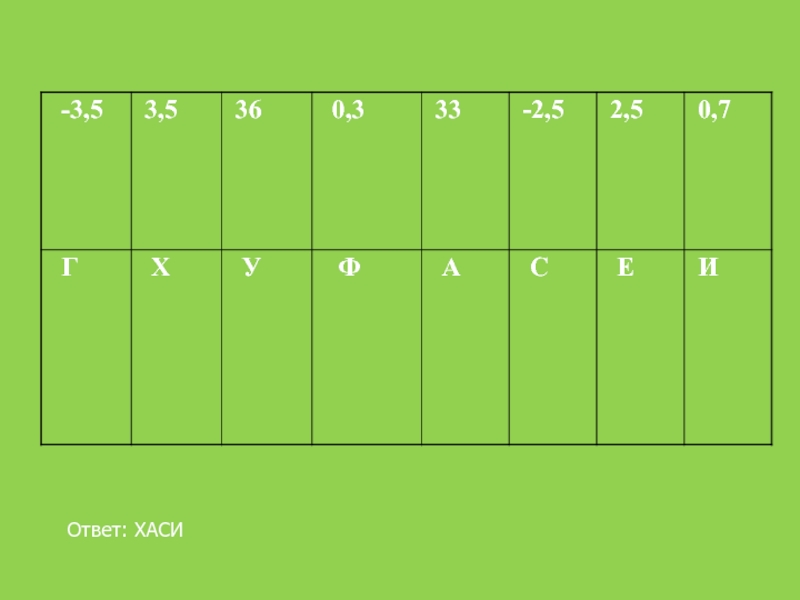
Выполните задания.
В восточных странах Китае, Корее, Японии и других,
люди едят
Часто их делают из бамбука, древесины,
слоновой кости и металла.
В Китае такие палочки называют «Куайцзы». Узнайте как палочки для еды называют в Японии.
Для этого выполните задания , учитывая.
Что (ап)- арифметическая прогрессии.
Зачеркните в таблице буквы,
соответствующие найденным ответам. 1) а1 =20; d =4. Найдите а5 ;
2) а1 =1,7 ; в =- 0,2 ; Найдите а8. 3) -8 ; -6,5; … Найдите а4 ;
4) а8 = -14; а10 = -9,5. Найдите d.
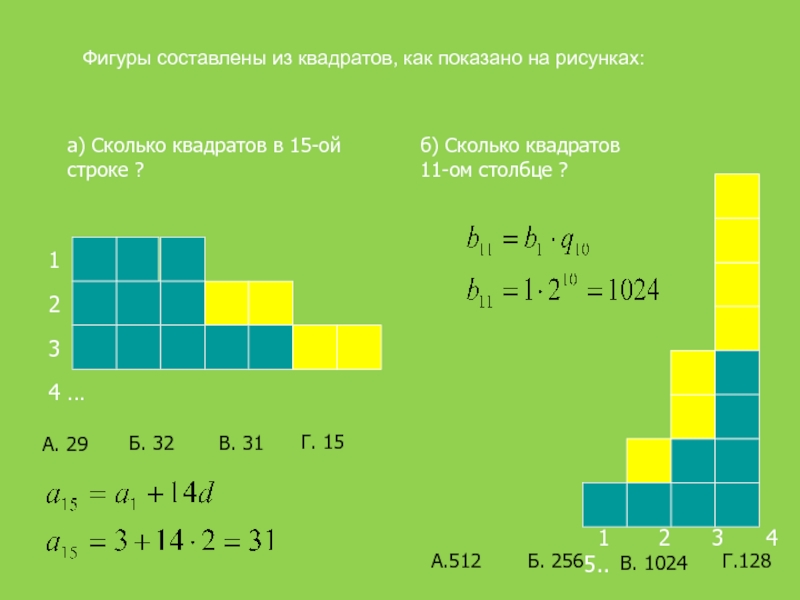
Слайд 15 Фигуры составлены из квадратов, как показано на рисунках:
а)
1
2
3
4 …
б) Сколько квадратов
11-ом столбце ?
1 2 3 4 5..
А. 29
А.512
Б. 32
В. 31
Г. 15
Б. 256
В. 1024
Г.128
Слайд 163.Вычислите сумму:
502 – 492 + 482 – 472 + 462
… + 42 – 32 +22 – 12;
1) Воспользуйтесь формулой разности квадратов:
(50-49)(50+49) + (48-47)(48+47) + (46-45)(46+45) +…
…+ (4-3)(4+3) + (2-1)(2+1);
2) Выполните действия в скобках:
99 + 95 + 91 + 87 +… + 7 + 3; эти числа образуют убывающую арифметическую прогрессию a1=99, an=3, n=25.
Ответ: сумма равна 1275.
Слайд 17
В старинной арифметике Магницкого есть следующая забавная задача.
Некто продал лошадь за 156 руб. Но покупатель, приобретя лошадь, раздумал её покупать и возвратил продавцу говоря:
-Нет мне расчёта покупать за эту цену лошадь, которая таких денег не стоит.
Тогда продавец предложил другие условия:
-Если по-твоему цена лошади высока, то купи только её подковные гвозди, лошадь же получишь тогда в придачу бесплатно.
Гвоздей в каждой подкове 6 шт. За первый гвоздь дай мне всего 1/4 коп., за второй 1/2 коп., за третий – 1 коп. и т.д.
Покупатель принял условия продавца, рассчитывая, что за гвозди придётся уплатить не более 10 руб.
На сколько покупатель проторговался?
Слайд 18
за 24 подковных гвоздя пришлось уплатить копеек.
Эти числа составляют геометрическую
прогрессию b1= , q=2, n=24. Найдите сумму
первых 24-х членов этой прогрессии:
То есть 41943 рубля. За такую цену и лошадь продать не жалко!
Слайд 19Задания из сборника предназначенного для подготовки к итоговой аттестации в новой
1) Пятый член арифметической прогрессии равен 8,4, а ее десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.
1) Число –3,8 является восьмым членом арифметической прогрессии (ап), а число –11 является ее двенадцатым членом. Является ли членом этой прогрессии число –30,8?
1) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.
1) В геометрической прогрессии b12 = З15 и b14 = З17. Найдите b1.
Слайд 20Ответы:
6.1 (20,4)
6.2. (является),
6.5. (6;8,2;10’4;12’6;14’8;17.),
6.8. (b1=34 или b1=
Слайд 21
Итог урока.
Сегодня на уроке мы повторили определения арифметической и геометрической прогрессий,
Наряду с простейшими задачами разобрали нестандартные задачи, поговорили о связи математики с жизнью. Чтобы преуспеть в бизнесе, нужно хорошо знать математику. Эти знания помогут избежать невыгодных сделок.
Рефлексия(На столе у учителя лежат смайлики, ученики оценивают себя и комментируют свой выбор)
Я готов!
Мне есть над чем поработать!
Я ничего не знаю!
Слайд 22Литература:
1.Глейзер Г.И.История математики в школе.-М.,Просвещение,1992г.
2.МакарычевЮ.Н .и др.Алгебра 9. – М., Просвещение
3.Коваленко В.Г. Дидактические игры на уроках математики .-
М., Просвещение ,1990г.
4.Газета «Математика» , Журнал «Математика в школе»
5.Учебный комплект “Алгебра 9” Часть 1.Учебник.,
Часть 2.Задачник. А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.
М.: “Мнемозина”.
6. “Алгебра. Сборник заданий для подготовки к итоговой
аттестации в 9 классе”
Л.В. Кузнецова. М.: “Просвещение”.
7. Ресурсы Интернет:
- festival.1september.ru;
- v-sp.ru›festival-pedagogicheskih…matematika.html;
- zavuch.info;
nsportal.ru.
И.т.д.