- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре 11 класс , решение задач ЕГЭ Геометрический смысл производной
Содержание
- 1. Презентация по алгебре 11 класс , решение задач ЕГЭ Геометрический смысл производной
- 2. Материальная точка движется прямолинейно по закону
- 3. Материальная точка движется прямолинейно по закону
- 4. Материальная точка M начинает движение из точки
- 5. Геометрический смысл производной, касательная
- 6. На рисунке изображен график функции y =
- 7. На рисунке изображен график функции y =
- 8. На рисунке изображен график производной функции f(x),
- 9. На рисунке изображен график производной функции f(x), определенной
- 10. На рисунке изображён график функции y=f(x) и
- 11. На рисунке изображён график функции y=f(x) и касательная к
Слайд 2Материальная точка движется прямолинейно по закону
Ответ: 60
Слайд 3Материальная точка движется прямолинейно по закону
Ответ: 20
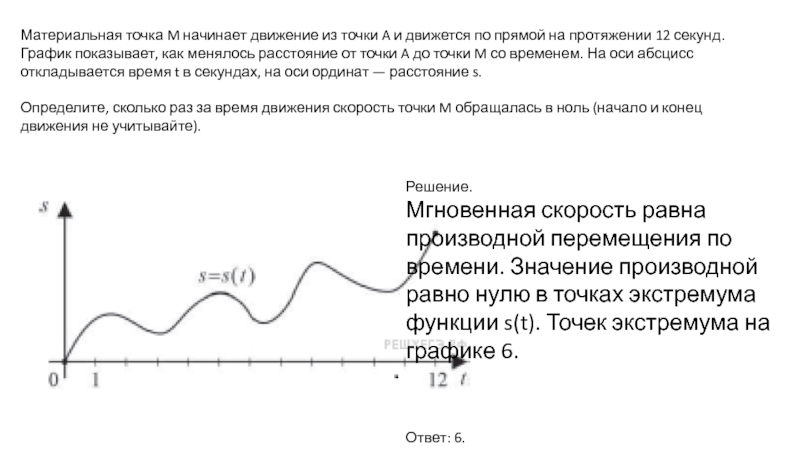
Слайд 4Материальная точка M начинает движение из точки A и движется по
Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
Решение.
Мгновенная скорость равна производной перемещения по времени. Значение производной равно нулю в точках экстремума функции s(t). Точек экстремума на графике 6.
Ответ: 6.
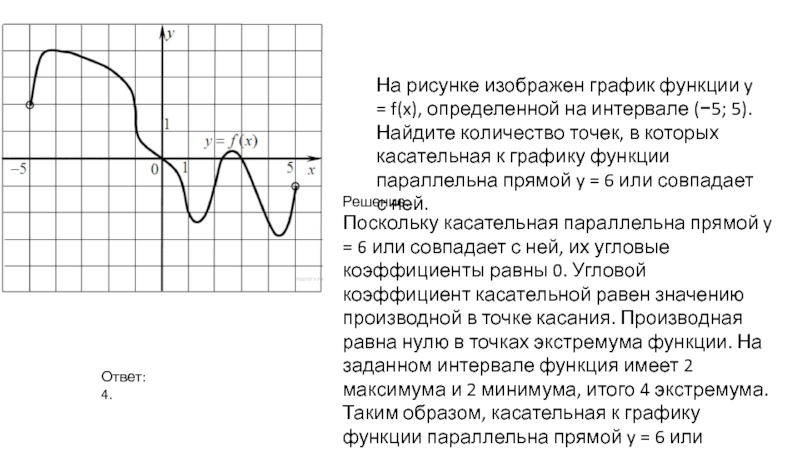
Слайд 6На рисунке изображен график функции y = f(x), определенной на интервале
Решение.
Поскольку касательная параллельна прямой y = 6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. Производная равна нулю в точках экстремума функции. На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Таким образом, касательная к графику функции параллельна прямой y = 6 или совпадает с ней в 4 точках.
Ответ: 4.
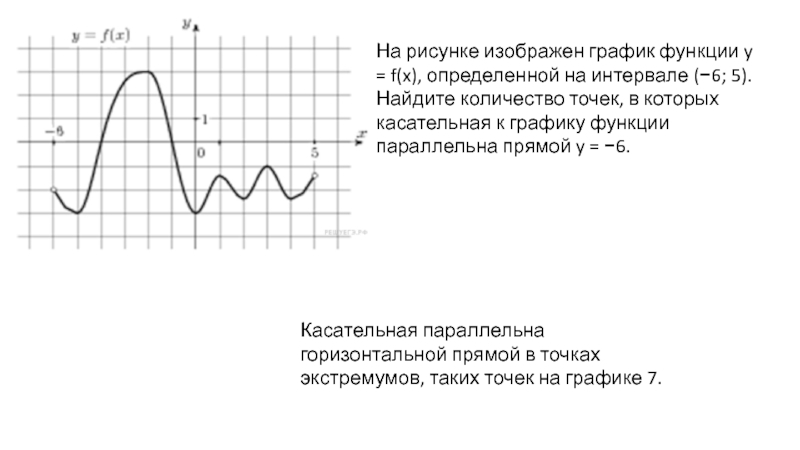
Слайд 7На рисунке изображен график функции y = f(x), определенной на интервале
Касательная параллельна горизонтальной прямой в точках экстремумов, таких точек на графике 7.
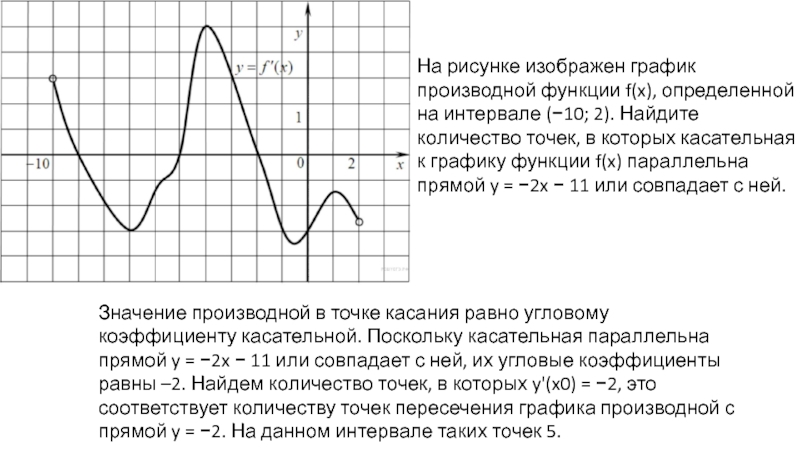
Слайд 8На рисунке изображен график производной функции f(x), определенной на интервале (−10;
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = −2x − 11 или совпадает с ней, их угловые коэффициенты равны –2. Найдем количество точек, в которых y'(x0) = −2, это соответствует количеству точек пересечения графика производной с прямой y = −2. На данном интервале таких точек 5.
Слайд 9На рисунке изображен график производной функции f(x), определенной на интервале (−9; 2).
Решение.Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = −x − 12 или совпадает с ней, их угловые коэффициенты равны –1. Найдем количество точек, в которых y'(x0) = −1, это соответствует количеству точек пересечения графика производной с прямой y = −1. На данном интервале таких точек 3.
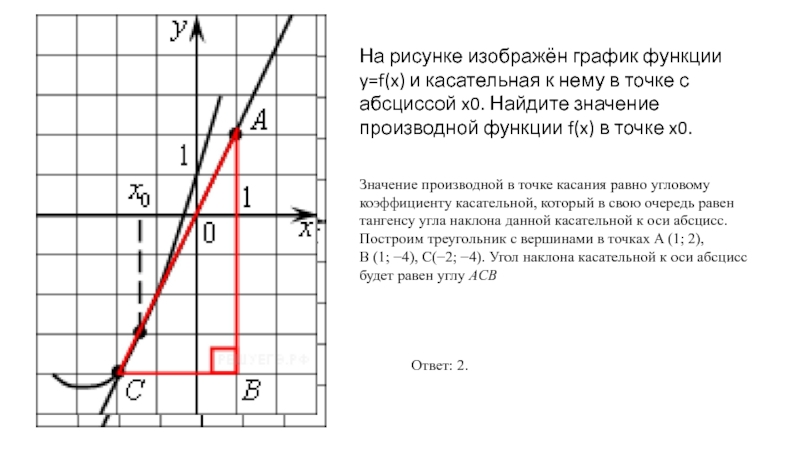
Слайд 10На рисунке изображён график функции y=f(x) и касательная к нему в
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен углу ACB
Ответ: 2.
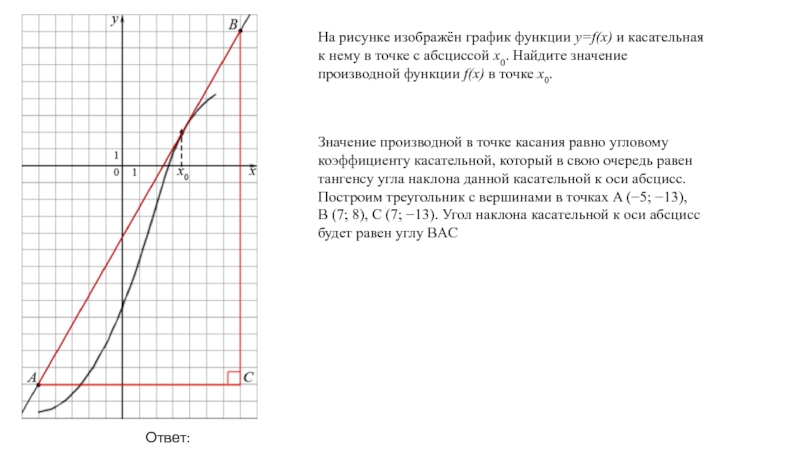
Слайд 11На рисунке изображён график функции y=f(x) и касательная к нему в точке с
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−5; −13), B (7; 8), C (7; −13). Угол наклона касательной к оси абсцисс будет равен углу BAC
Ответ: 1,75.