Презентация, доклад по алгебре 11 класс на тему Понятие корня н-й степени из действительного числа

Содержание

1. Презентация по алгебре 11 класс на тему Понятие корня н-й степени из действительного числа
2. Какая кривая является графиком функции y =
3. Рассмотрим уравнение x⁵ = 1.Построим графики
4. Определение 1 :Корнем n – й степени
5. Операция извлечение корня является обратной по отношению
6. Пример 1:Вычислить: а) √ 49; б) √
7. ИтакВывод:Корень чётной степени имеет смысл (т.е. определён)
8. Возведём обе части уравнения в куб:а)б)Возведём обе
9. Домашнее задание:§ 6, № 33.5-33.12Удачи!!!!!

Какая кривая является графиком функции y = x²?Какая кривая является графиком функции y = x⁴ ?Рассмотрим уравнение x⁴ = 1.Построим графики функций y = x⁴ и y = 1.Ответ: x = 1, x = -1.Аналогично:x⁴

Главная
Алгебра
Презентация по алгебре 11 класс на тему Понятие корня н-й степени из действительного числа

Слайд 1Понятие корня n – й степени
из действительного числа.

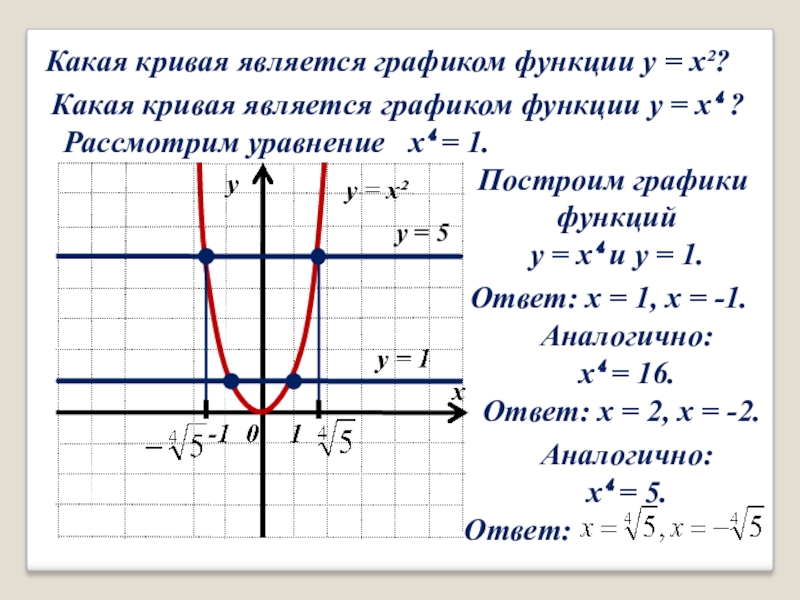
Слайд 2Какая кривая является графиком функции y = x²?
Какая кривая является графиком

функции y = x⁴ ?

Рассмотрим уравнение x⁴ = 1.

Построим графики
функций
y = x⁴ и y = 1.

Ответ: x = 1, x = -1.

Аналогично:
x⁴ = 16.

Ответ: x = 2, x = -2.

Аналогично:
x⁴ = 5.

y = 5

Ответ:

Какая кривая является графиком функции y = x²?Какая кривая является графиком функции y = x⁴ ?Рассмотрим уравнение

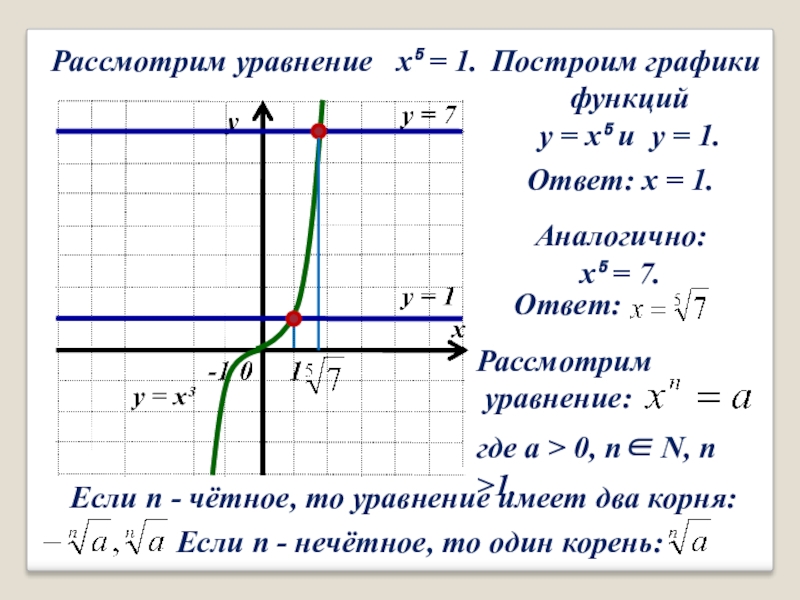
Слайд 3Рассмотрим уравнение x⁵ = 1.
Построим графики
функций
y = x⁵

и y = 1.

Аналогично:
x⁵ = 7.

Ответ: x = 1.

Ответ:

Рассмотрим
уравнение:

где a > 0, n∈ N, n >1.

Если n - чётное, то уравнение имеет два корня:

Если n - нечётное, то один корень:

Рассмотрим уравнение x⁵ = 1.Построим графики функций y = x⁵ и y = 1.Аналогично:x⁵ = 7.Ответ:

Слайд 4Определение 1 :
Корнем n – й степени из неотрицательного числа a

(n = 2,3,4,5,…) называют такое неотрицательное
число, которое при возведении в степень n даёт
в результате число a.

Это число обозначают:

- подкоренное выражение

-показатель корня

Операцию нахождения корня из неотрицательного
числа называют извлечением корня.

Определение 1 :Корнем n – й степени из неотрицательного числа a (n = 2,3,4,5,…) называют такое неотрицательное

Слайд 5Операция извлечение корня является обратной
по отношению к возведению в соответствующую

степень.

5² = 25

10³ = 1000

0,3⁴ = 0,0081

Слайд 6Пример 1:
Вычислить: а) √ 49; б) √ 0,125; в) √ 0

; г) √ 17

Решение:

а) √ 49 = 7, так как 7 > 0 и 7² = 49;

б) √ 0,125 = 0,5, так как 0,5 > 0 и 0,5³ = 0,125;

в) √ 0 ;

г) √ 17 ≈ 2,03

Определение 2 :

Корнем нечётной степени n из отрицательного
числа a (n = 3,5,…) называют такое
отрицательное число, которое при возведении
в степень n даёт в результате число a.

Пример 1:Вычислить: а) √ 49; б) √ 0,125; в) √ 0 ; г) √ 17374Решение:а) √ 49

Слайд 7Итак
Вывод:
Корень чётной степени имеет смысл
(т.е. определён) только для неотрицательного
подкоренного

выражения; корень нечётной степени
имеет смысл для любого подкоренного выражения.

Пример 2:

Решите уравнения:

ИтакВывод:Корень чётной степени имеет смысл (т.е. определён) только для неотрицательного подкоренного выражения; корень нечётной степени имеет смысл

Слайд 8Возведём обе части уравнения в куб:
а)
б)
Возведём обе части уравнения в четвёртую

степень:

в)

Решений нет. Почему?

г)

Возведём обе части уравнения в шестую степень:

Возведём обе части уравнения в куб:а)б)Возведём обе части уравнения в четвёртую степень:в)Решений нет. Почему?г)Возведём обе части уравнения

Слайд 9Домашнее задание:
§ 6, № 33.5-33.12
Удачи!!!!!

Скачать презентацию

Презентация, доклад по алгебре 11 класс на тему Понятие корня н-й степени из действительного числа

Содержание

Слайд 1Понятие корня n – й степени
из действительного числа.

Слайд 2Какая кривая является графиком функции y = x²?
Какая кривая является графиком

Слайд 3Рассмотрим уравнение x⁵ = 1.
Построим графики
функций
y = x⁵

Слайд 4Определение 1 :
Корнем n – й степени из неотрицательного числа a

Слайд 5Операция извлечение корня является обратной
по отношению к возведению в соответствующую

Слайд 6Пример 1:
Вычислить: а) √ 49; б) √ 0,125; в) √ 0

Слайд 7Итак
Вывод:
Корень чётной степени имеет смысл
(т.е. определён) только для неотрицательного
подкоренного

Слайд 8Возведём обе части уравнения в куб:
а)
б)
Возведём обе части уравнения в четвёртую

Слайд 9Домашнее задание:
§ 6, № 33.5-33.12
Удачи!!!!!

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по алгебре 11 класс на тему Понятие корня н-й степени из действительного числа

Содержание

Слайд 1Понятие корня n – й степени из действительного числа.

Слайд 2Какая кривая является графиком функции y = x²?Какая кривая является графиком

Слайд 3Рассмотрим уравнение x⁵ = 1.Построим графики функций y = x⁵

Слайд 4Определение 1 :Корнем n – й степени из неотрицательного числа a

Слайд 5Операция извлечение корня является обратной по отношению к возведению в соответствующую

Слайд 6Пример 1:Вычислить: а) √ 49; б) √ 0,125; в) √ 0

Слайд 7ИтакВывод:Корень чётной степени имеет смысл (т.е. определён) только для неотрицательного подкоренного

Слайд 8Возведём обе части уравнения в куб:а)б)Возведём обе части уравнения в четвёртую

Слайд 9Домашнее задание:§ 6, № 33.5-33.12Удачи!!!!!

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Понятие корня n – й степени
из действительного числа.

Слайд 2Какая кривая является графиком функции y = x²?
Какая кривая является графиком

Слайд 3Рассмотрим уравнение x⁵ = 1.
Построим графики
функций
y = x⁵

Слайд 4Определение 1 :
Корнем n – й степени из неотрицательного числа a

Слайд 5Операция извлечение корня является обратной
по отношению к возведению в соответствующую

Слайд 6Пример 1:
Вычислить: а) √ 49; б) √ 0,125; в) √ 0

Слайд 7Итак
Вывод:
Корень чётной степени имеет смысл
(т.е. определён) только для неотрицательного
подкоренного

Слайд 8Возведём обе части уравнения в куб:
а)
б)
Возведём обе части уравнения в четвёртую

Слайд 9Домашнее задание:
§ 6, № 33.5-33.12
Удачи!!!!!