- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре 10 класс Степенная функция
Содержание
- 1. Презентация по алгебре 10 класс Степенная функция
- 2. Степенная функция
- 3. Цель урока:Повторить , систематизировать и расширить знания по теме «Степенная функция»
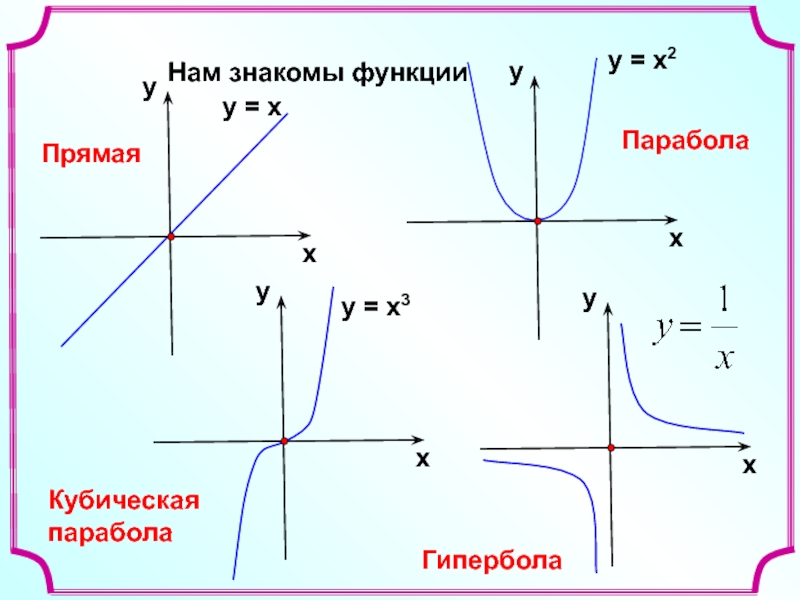
- 4. Нам знакомы функцииПрямаяПараболаКубическая параболаГипербола
- 5. Все эти функции являются частными случаями степенной
- 6. Показатель р = 2n – четное натуральное
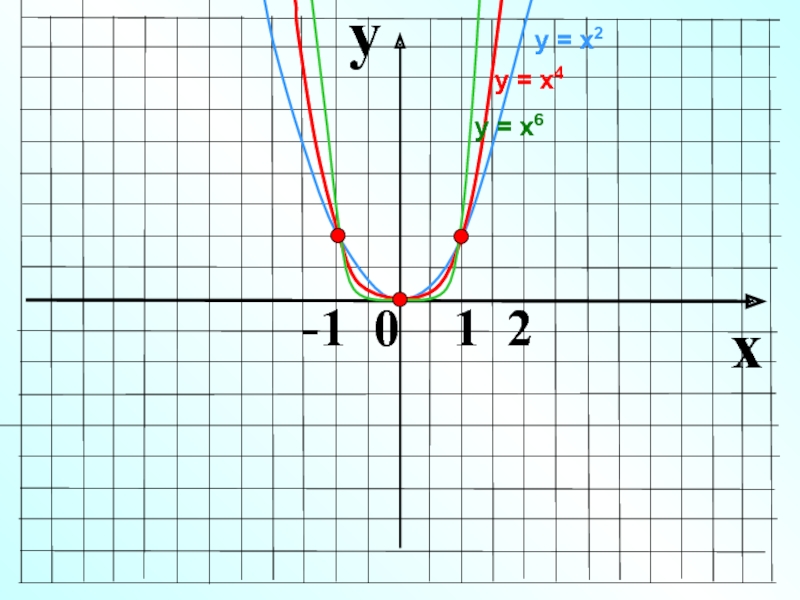
- 7. yx -1 0 1 2у = х2 у = х6у = х4
- 8. Показатель р = 2n-1 – нечетное
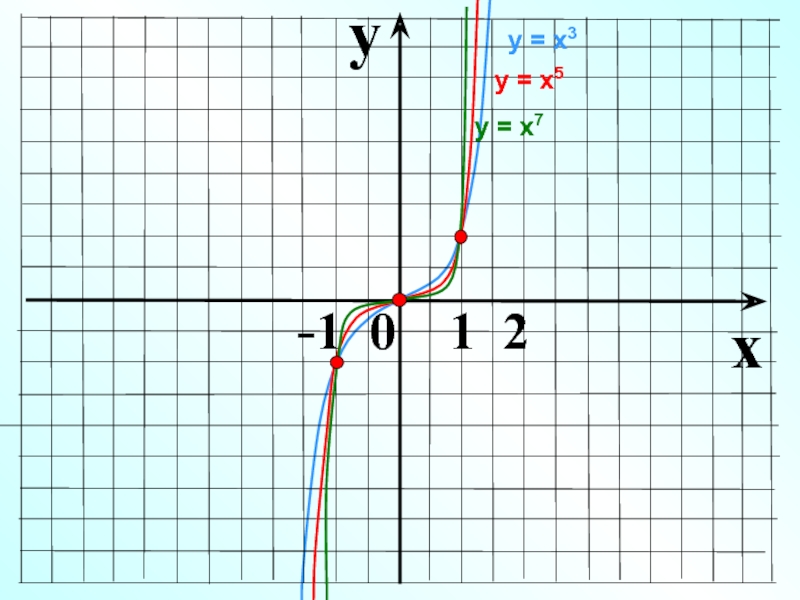
- 9. yx -1 0 1 2у = х3 у = х7у = х5
- 10. Показатель р = – 2n, где n
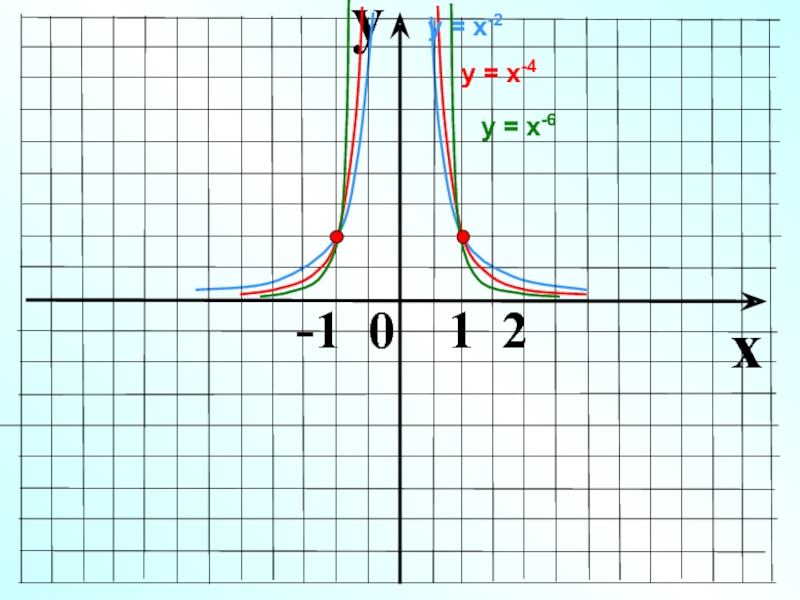
- 11. yx -1 0 1 2у = х-4у = х-2у = х-6
- 12. Показатель р = – (2n-1), где n
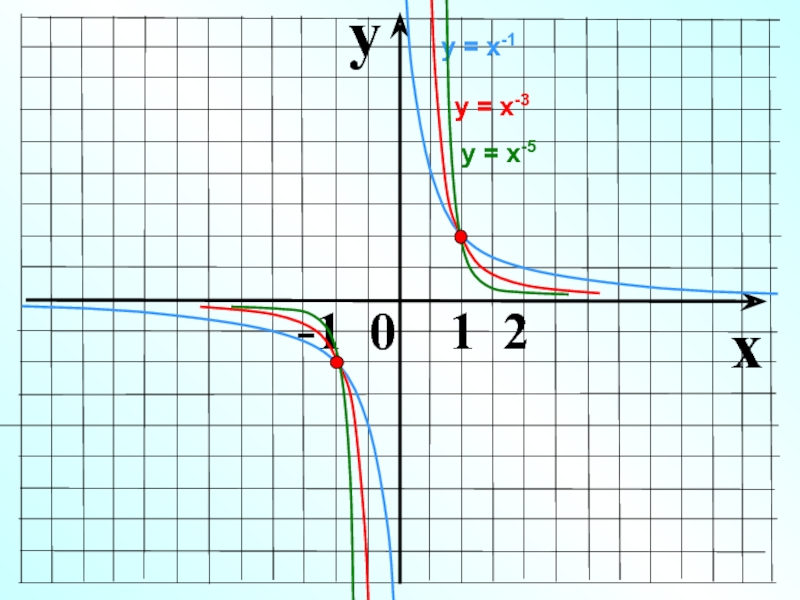
- 13. yx -1 0 1 2у = х-1у = х-3у = х-5
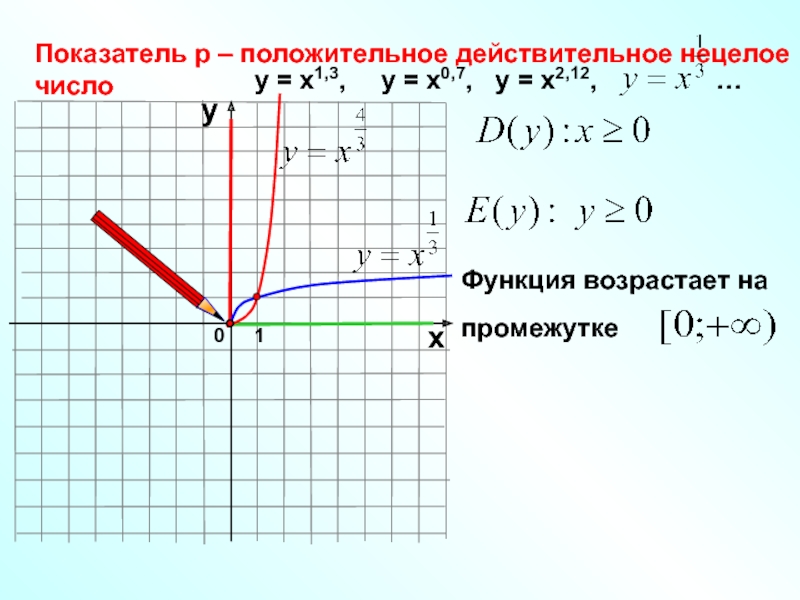
- 14. 0Показатель р – положительное действительное нецелое число1хуу
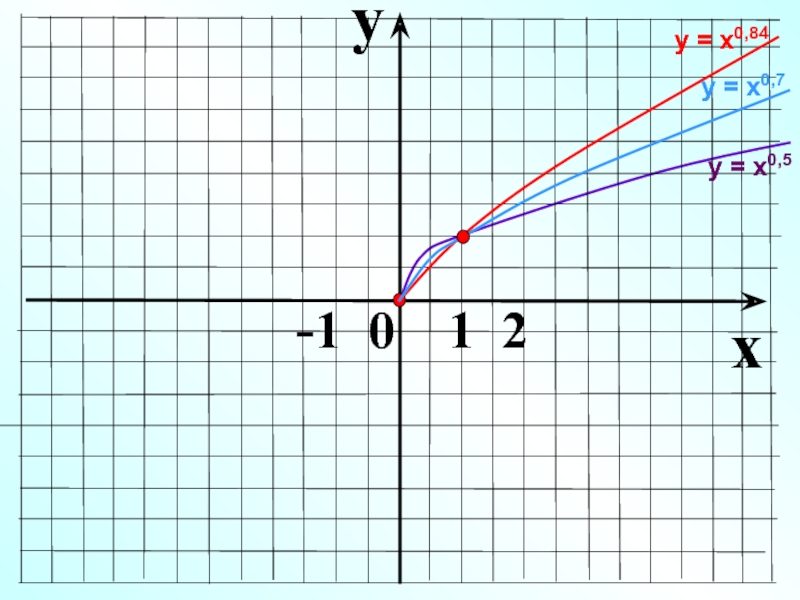
- 15. yx -1 0 1 2у = х0,5
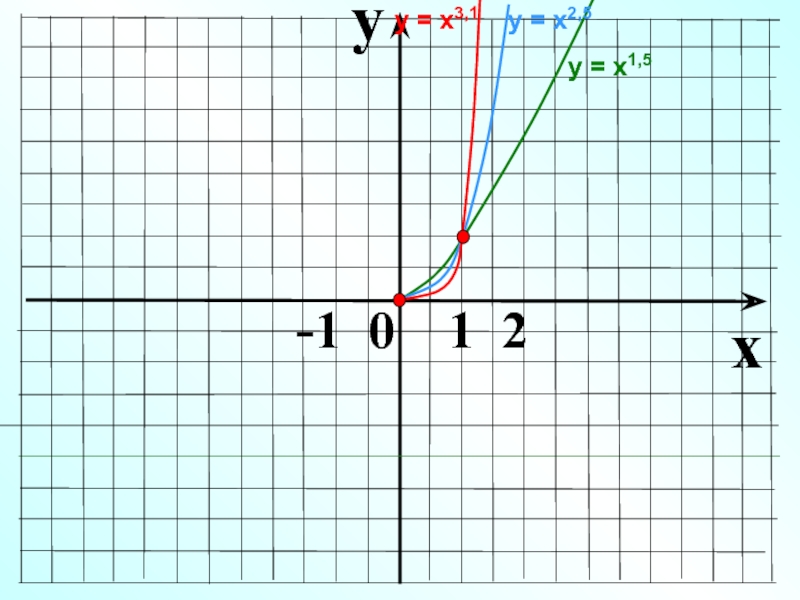
- 16. yx -1 0 1 2
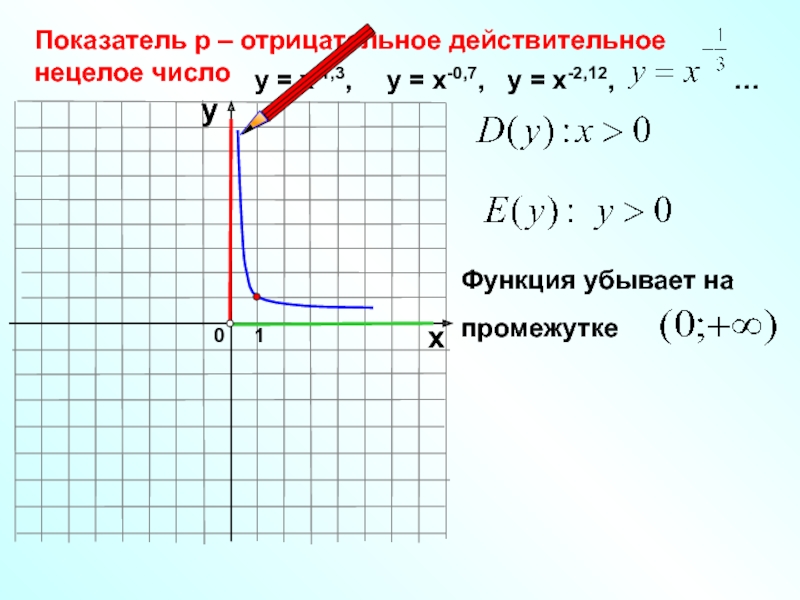
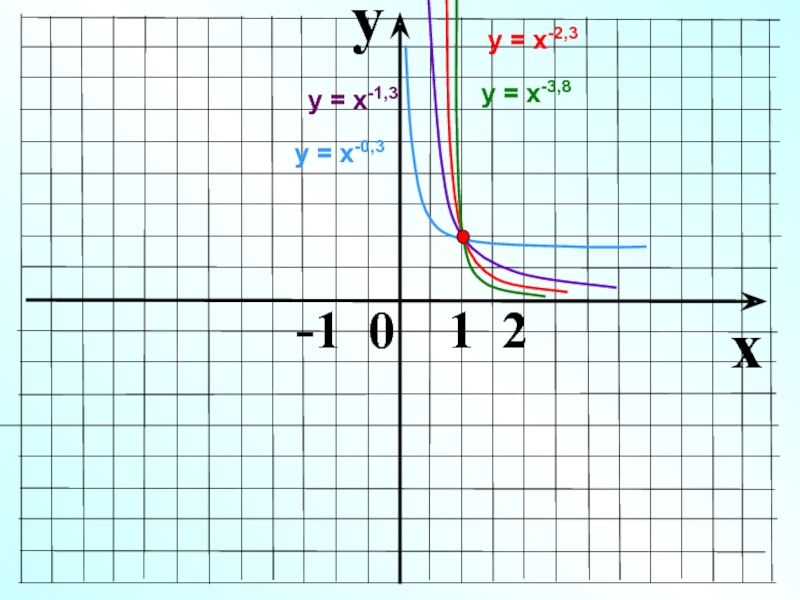
- 17. 0Показатель р – отрицательное действительное нецелое число1хуу
- 18. yx -1 0 1 2
- 19. Историческая справка
- 20. Физ.минутка
- 21. Стимуляция деятельности головного мозгаНос — важнейшая рефлексогенная
- 22. Сгибают кончик носа влево.
- 23. Графическое лото(Работаем на доске)
- 24. Задача ЕГЭ На учебном полигоне произведён выстрел
- 25. Слайд 25
- 26. Домашнее задание:Выучить опорный конспект.№3.17,3.18Дополнительно № 3.19, подобрать
- 27. Общий вид степенной функции:Если показатель р
- 28. Самостоятельная работа
- 29. Дружить наукам можно вечно, Вселенная ведь бесконечна.
Слайд 5Все эти функции являются частными случаями степенной функции
у
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень хр.
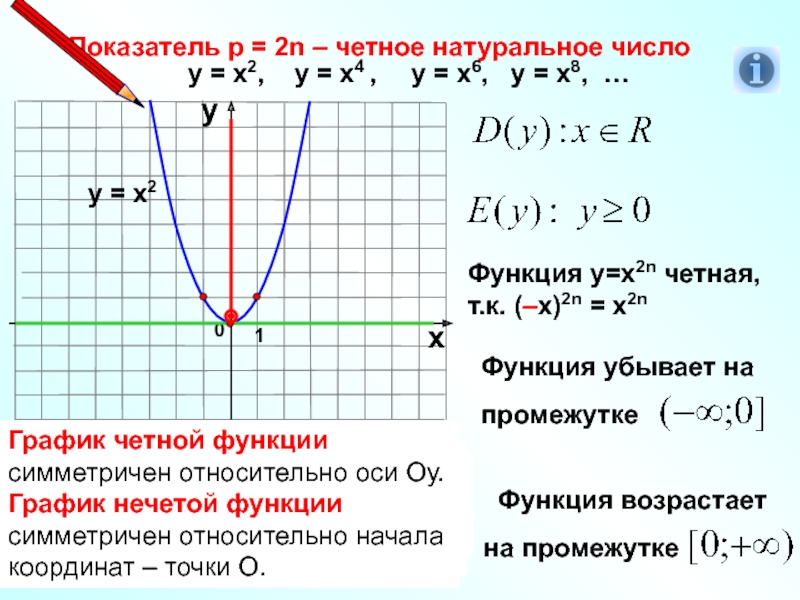
Слайд 6Показатель р = 2n – четное натуральное число
1
0
х
у
у = х2,
у = х2
Функция у=х2n четная,
т.к. (–х)2n = х2n
Область определения функции –
значения, которые может принимать переменная х
Область значений функции –
множество значений,
которые может принимать
переменная у
График четной функции симметричен относительно оси Оу.
График нечетой функции симметричен относительно начала координат – точки О.
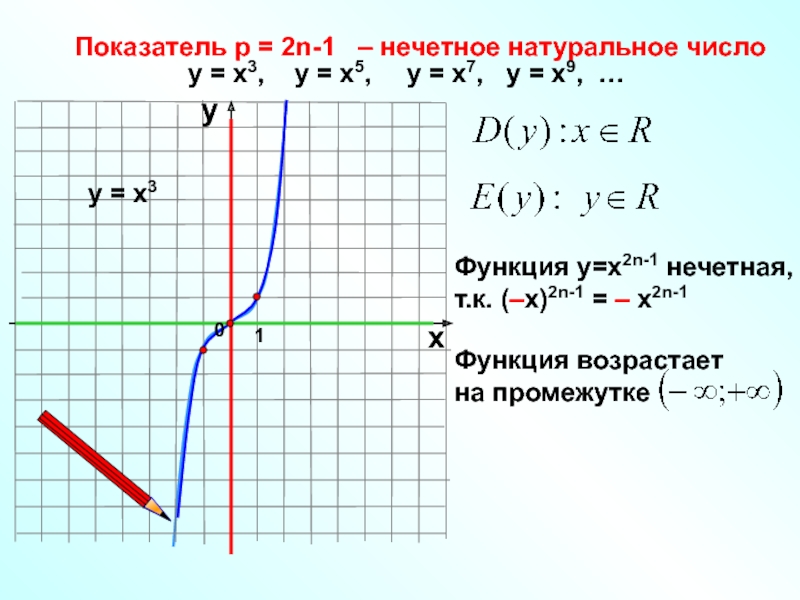
Слайд 8Показатель р = 2n-1 – нечетное натуральное число
1
х
у
у = х3,
у = х3
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
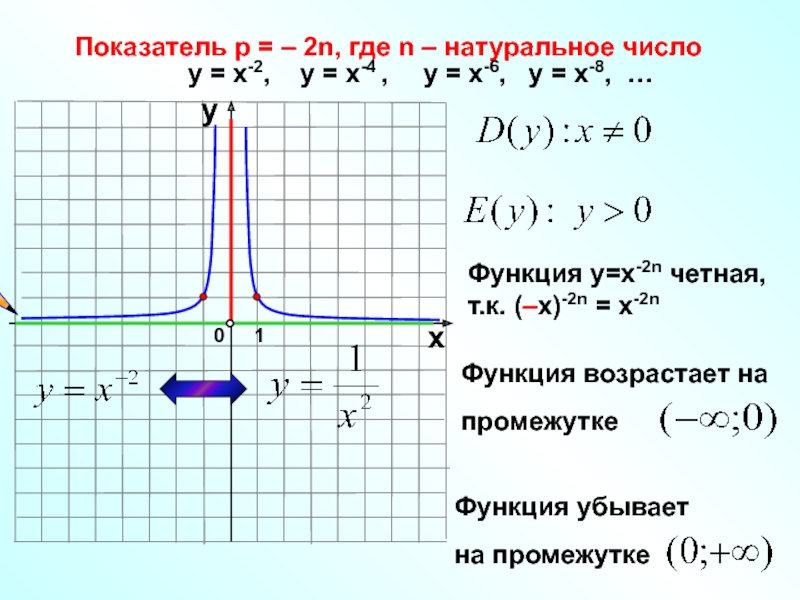
Слайд 10Показатель р = – 2n, где n – натуральное число
1
0
х
у
у =
Функция у=х-2n четная,
т.к. (–х)-2n = х-2n
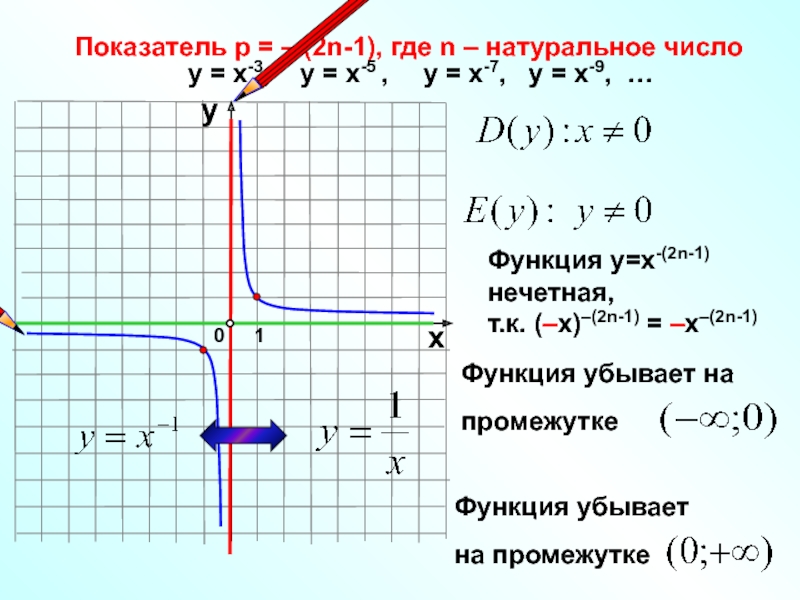
Слайд 12Показатель р = – (2n-1), где n – натуральное число
1
0
х
у
у =
Функция у=х-(2n-1) нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Слайд 140
Показатель р – положительное действительное нецелое число
1
х
у
у = х1,3,
Слайд 170
Показатель р – отрицательное действительное
нецелое число
1
х
у
у = х-1,3,
Слайд 21Стимуляция деятельности головного мозга
Нос — важнейшая рефлексогенная зона лица. Он связан
УУУУ
Указательным и средним пальцами сгибают кончик носа вправо
Указательным или средним пальцем нажимают на кончик носа
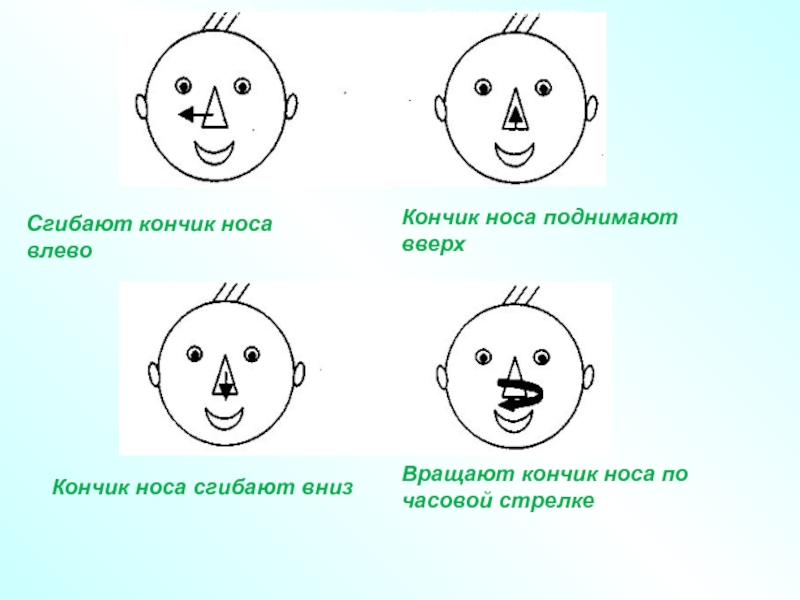
Слайд 22Сгибают кончик носа влево. Кончик носа поднимают вверх.
Сгибают
Сгибают кончик носа влево
Кончик носа поднимают вверх
Кончик носа сгибают вниз
Вращают кончик носа по
часовой стрелке
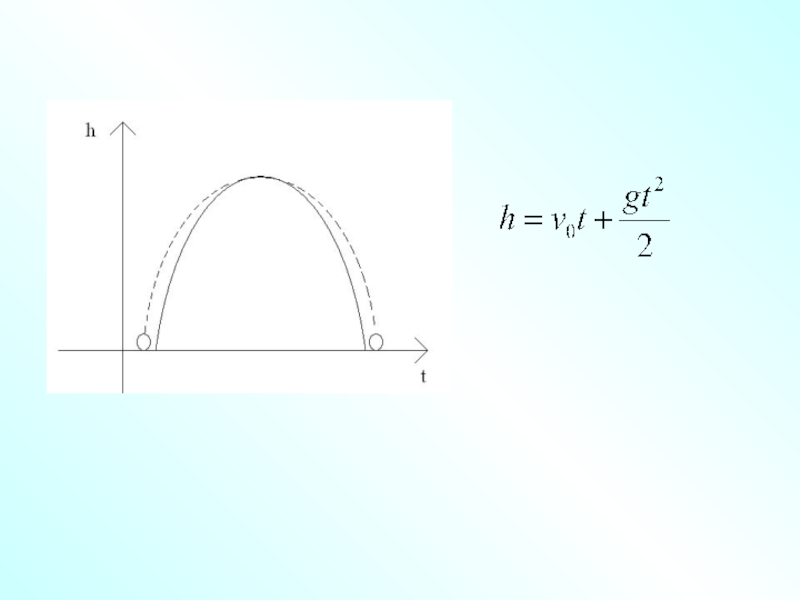
Слайд 24Задача ЕГЭ
На учебном полигоне произведён выстрел из зенитного орудия в
Слайд 26Домашнее задание:
Выучить опорный конспект.
№3.17,3.18
Дополнительно № 3.19, подобрать задачи из жизни и
Слайд 27
Общий вид степенной функции:
Если показатель р –чётное число
Если показатель р
Если показатель р – дробное число
у = хр, где р – заданное действительное число
График – парабола
График – кубическая парабола
График – ветка гиперболы
Подведём итог:
Слайд 29Дружить наукам можно вечно, Вселенная ведь бесконечна. Спасибо всем вам за урок, А главное,