- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре 10 класс
Содержание
- 1. Презентация по алгебре 10 класс
- 2. Построение графика степенной функции
- 3. Цель урока:продолжить формирование наглядных представлений о графиках
- 4.
- 5. Степенными функциями называются функции вида у = хp, где p – заданное рациональное число
- 6. yx -1 0 1 2у
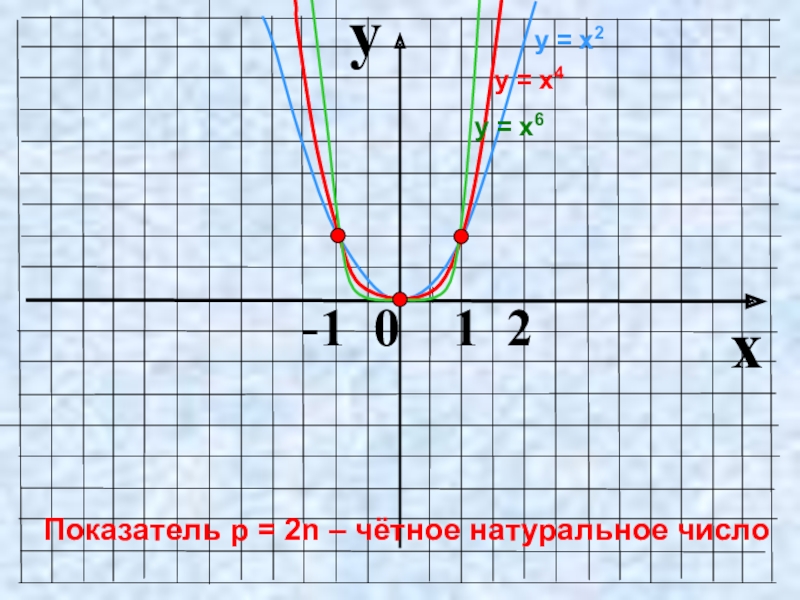
- 7. Показатель p = 2n – чётное натуральное
- 8. yx -1 0 1 2у
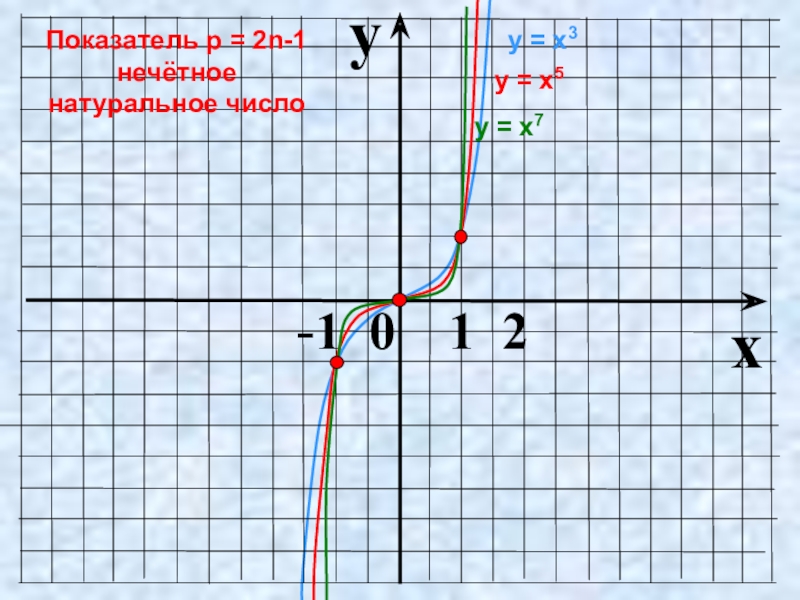
- 9. Показатель p = 2n-1 – нечётное
- 10. yx -1 0 1 2у
- 11. Показатель p = – (2n-1), где n
- 12. yx -1 0 1 2у
- 13. Показатель p = – 2n, где n
- 14. yx -1 0 1 2у
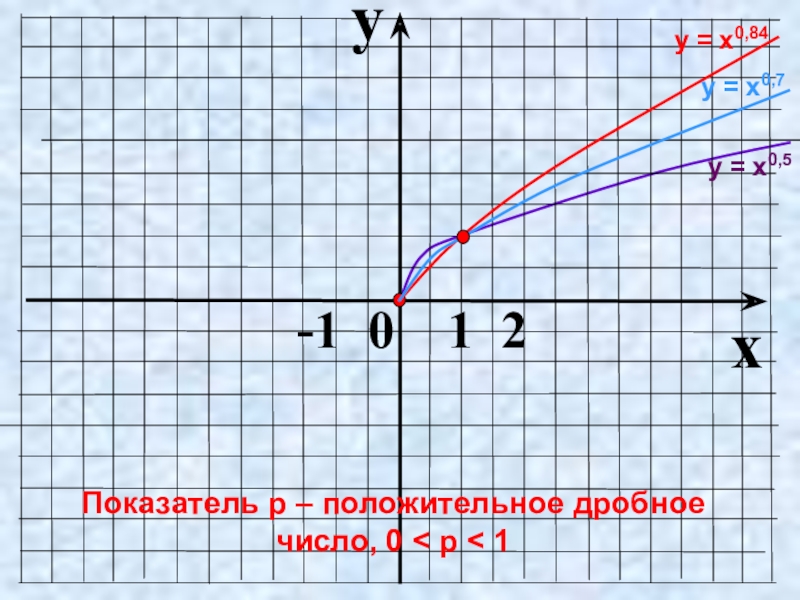
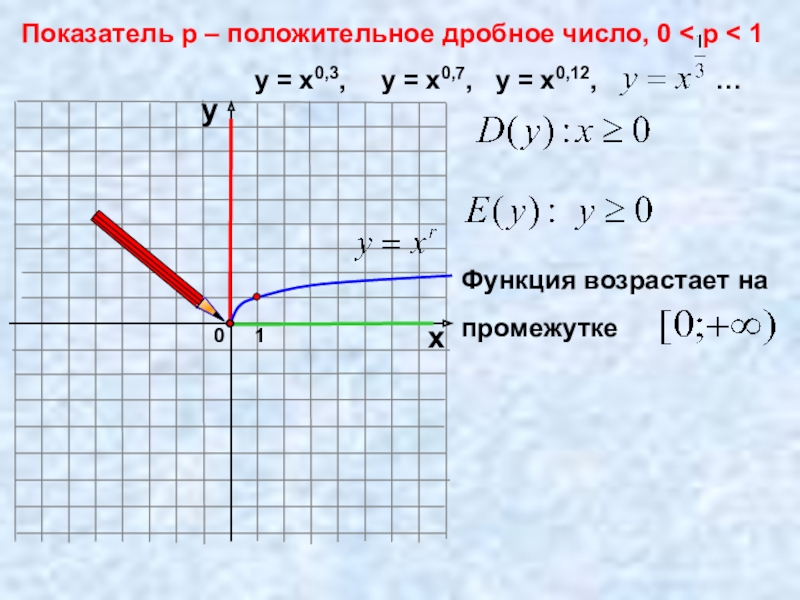
- 15. 0Показатель p – положительное дробное число, 0
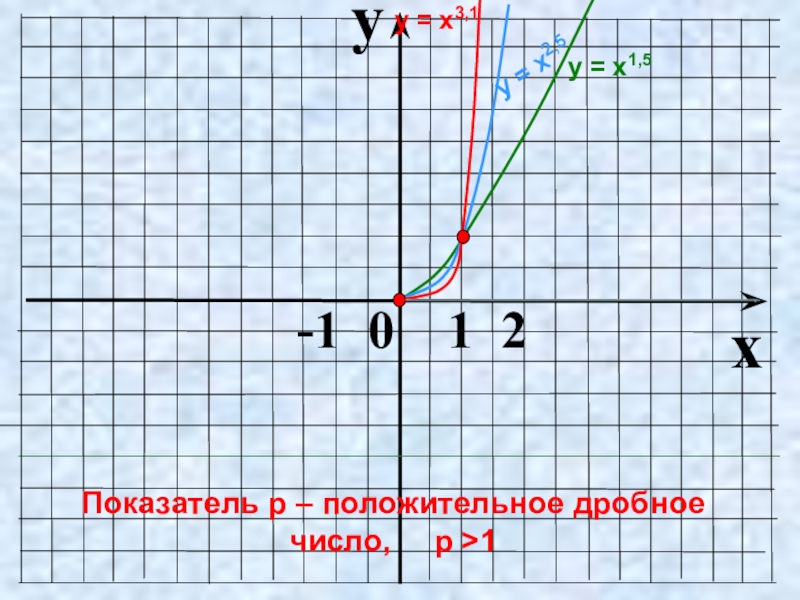
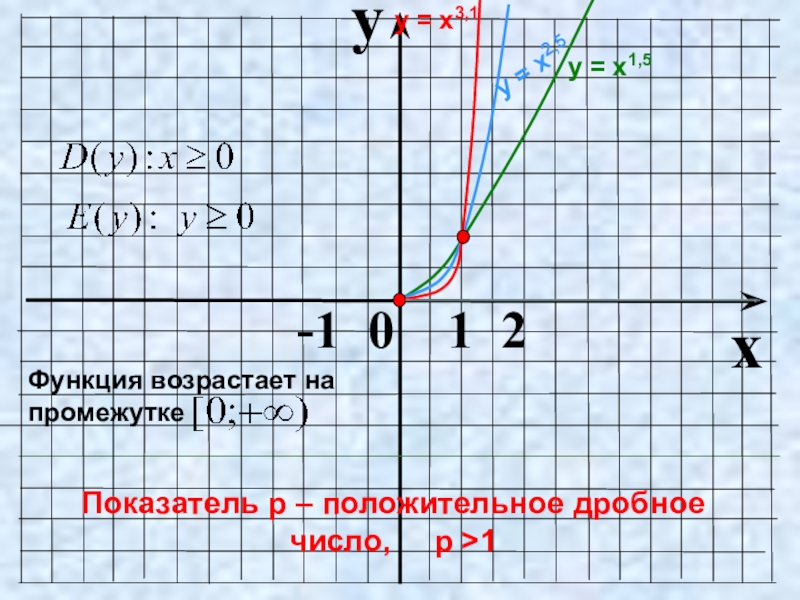
- 16. yx -1 0 1 2Показатель p – положительное дробное число, p >1
- 17. yx -1 0 1 2Показатель
- 18. yx -1 0 1 2Показатель
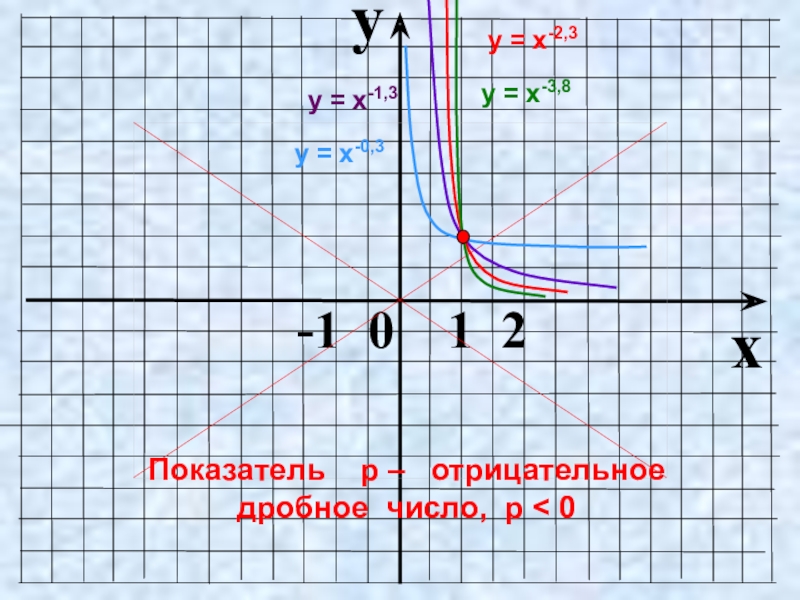
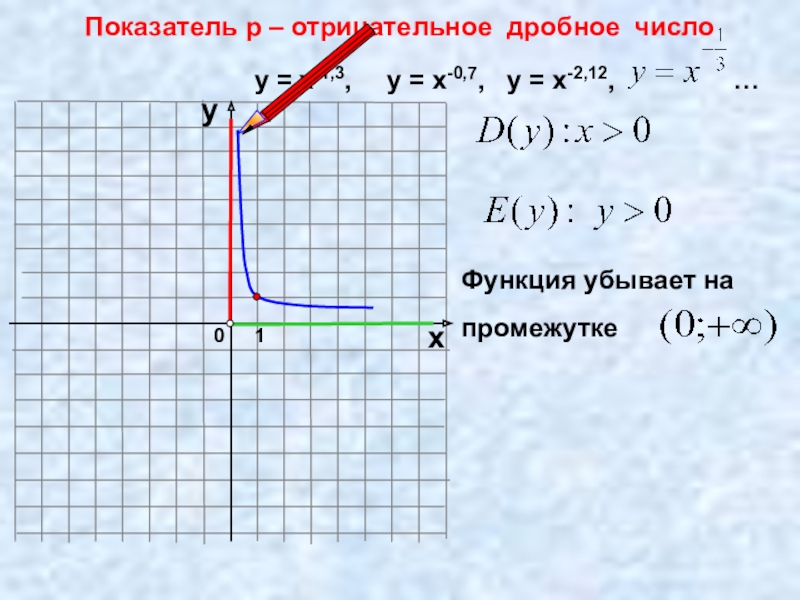
- 19. 0Показатель p – отрицательное дробное число1хуу =
- 20. Слайд 20
- 21. ПРАВИЛЬНЫЙ ОТВЕТ: 796 514 283
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. ПРАВИЛЬНЫЙ ОТВЕТ: 1567
- 27. Преобразования графиков степенных функций
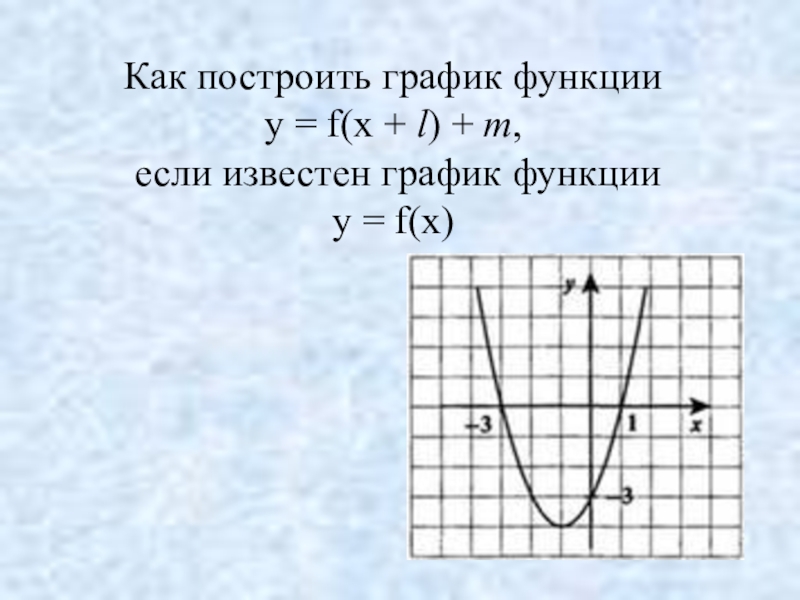
- 28. Как построить график функции y = f(x + l), если известен график функции y = f(x)
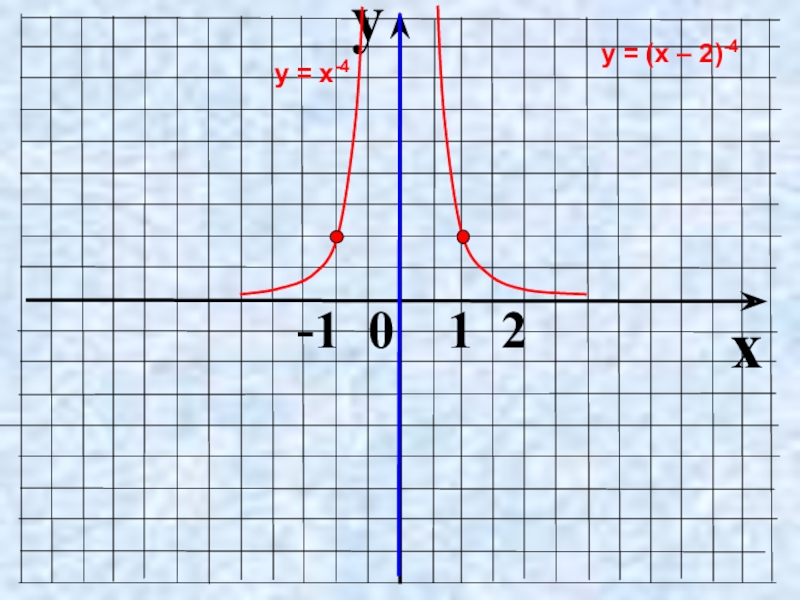
- 29. yx -1 0 1 2у = х-4у = (х – 2)-4
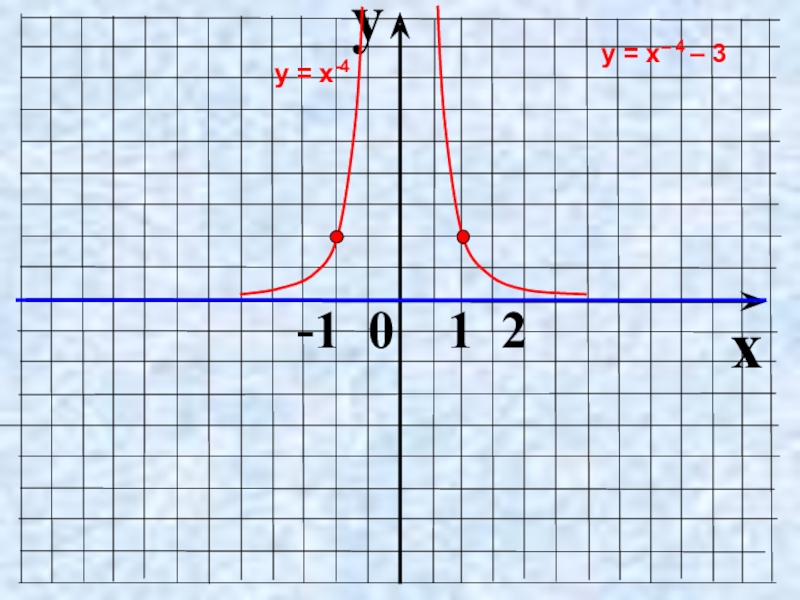
- 30. Как построить график функции y = f(x) + m, если известен график функции y = f(x)
- 31. yx -1 0 1 2у = х-4у = х– 4 – 3
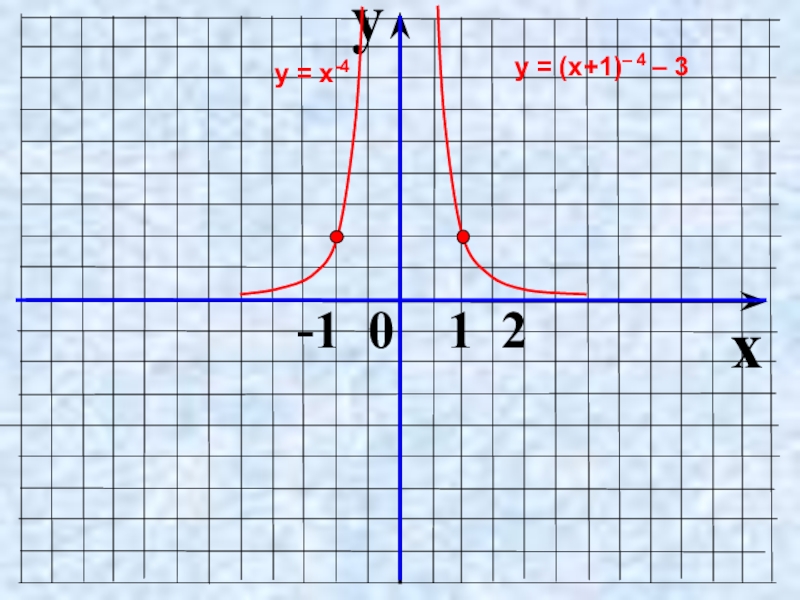
- 32. Как построить график функции y = f(x
- 33. yx -1 0 1 2у = х-4у = (х+1)– 4 – 3
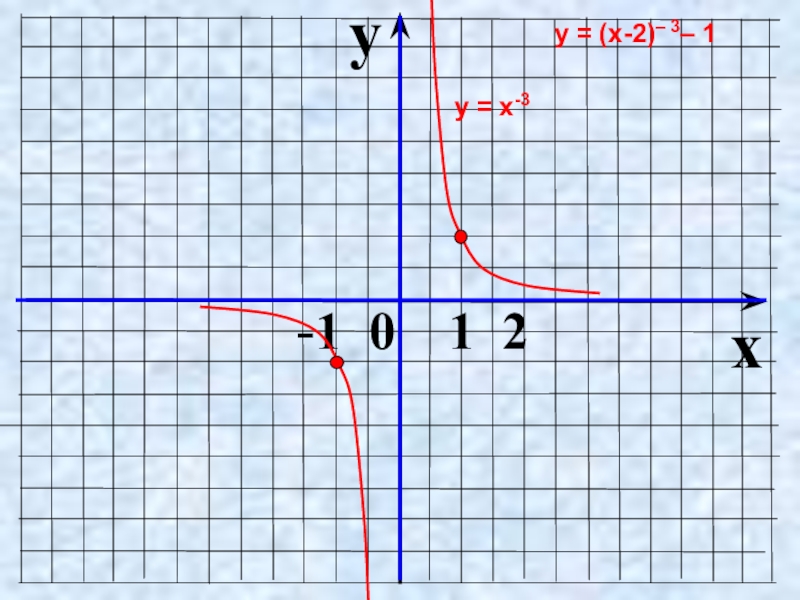
- 34. yx -1 0 1 2у = х-3у = (х-2)– 3– 1
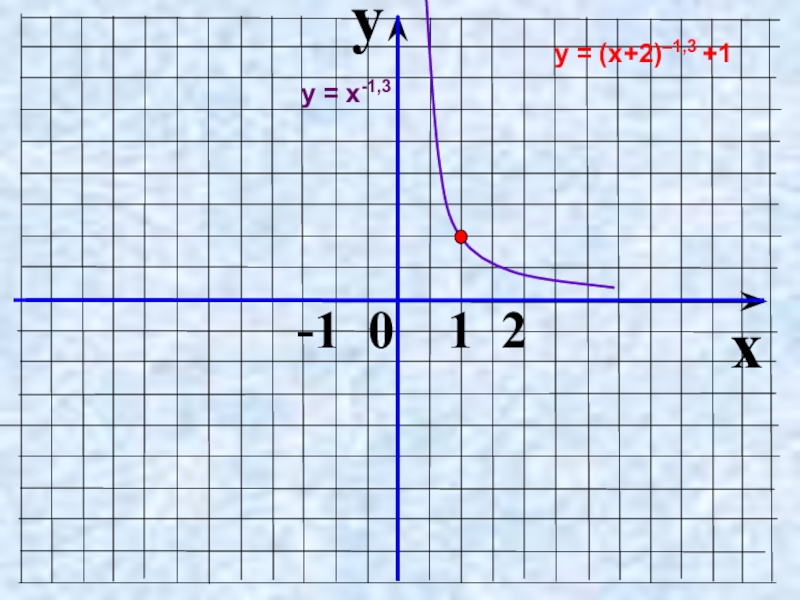
- 35. yx -1 0 1 2у = (х+2)–1,3 +1у = х-1,3
- 36. -Для того, чтобы построить график данной функции,
- 37. -Для того, чтобы построить график данной функции,
- 38. -Для того, чтобы построить график данной функции,
- 39. -Для того, чтобы построить график данной функции,
- 40. -Для того, чтобы построить график данной функции,
- 41. -Для того, чтобы построить график данной функции,
- 42. -Для того, чтобы построить график данной функции,
- 43. -Для того, чтобы построить график данной функции,
- 44. -Для того, чтобы построить график данной функции,
- 45. Слайд 45
- 46. Слайд 46
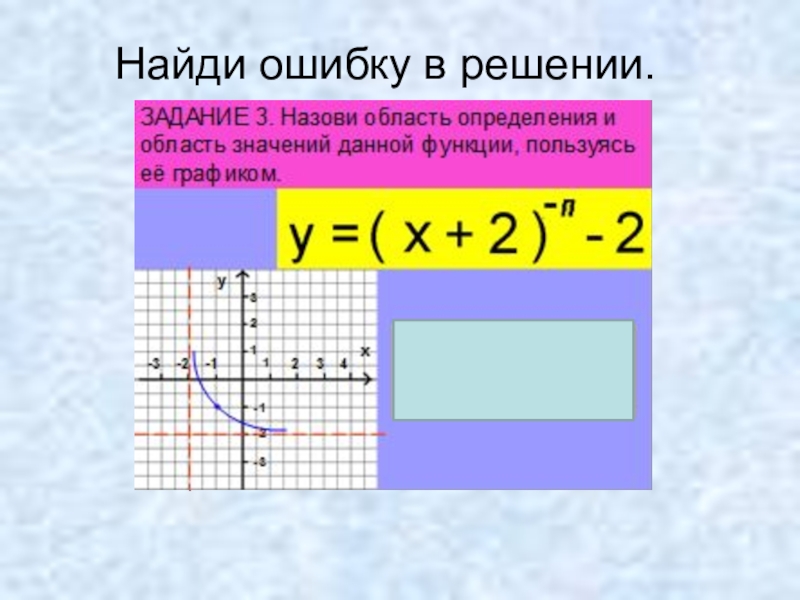
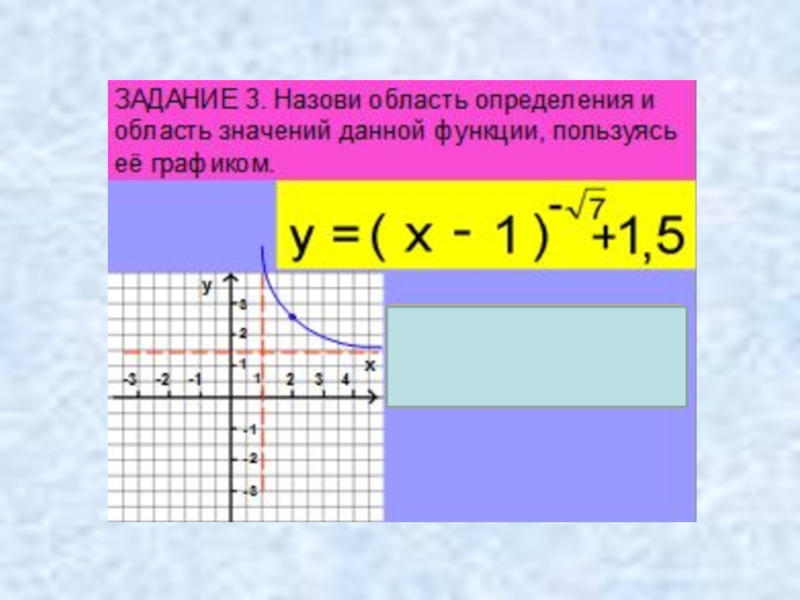
- 47. Найди ошибку в решении.
- 48. Слайд 48
- 49. Слайд 49
- 50. Решение задач по учебнику на стр. 183-184№557 (1, 2)№567 ( 1, 3)
- 51. Проверим свои знания: Математический диктант с последующей
- 52. О т в е т .
- 53. РЕФЛЕКСИЯ Что вы ожидали от работы на
- 54. Оцените свою работу на урокеНапишите свою фамилию
- 55. Домашнее задание
- 56. Слайд 56
Построение графика степенной функции
Слайд 3Цель урока:
продолжить формирование наглядных представлений о графиках степенной функции, способах построения
графиков с помощью движений графика исходной функции;
развить умение
строить график степенной функции,
определять по нему область определения и множество значений функции;
способствовать формированию объективной самооценки.
развить умение
строить график степенной функции,
определять по нему область определения и множество значений функции;
способствовать формированию объективной самооценки.
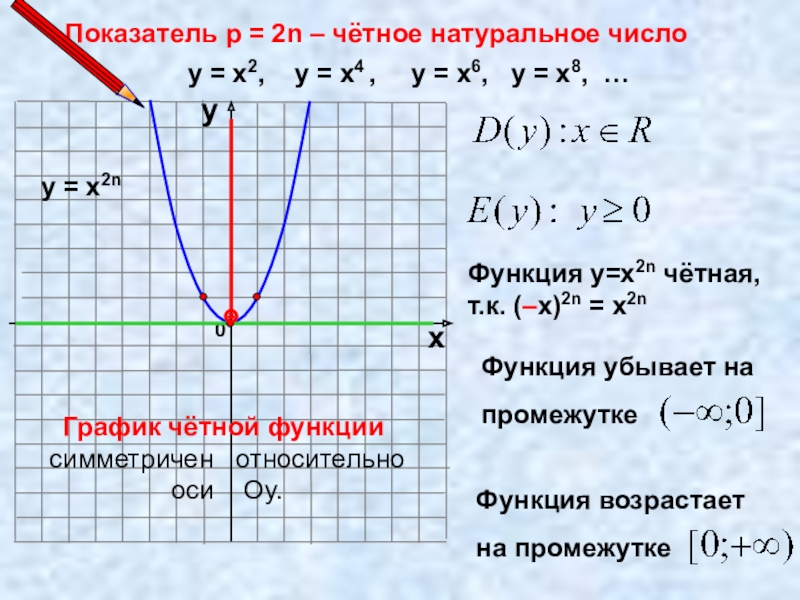
Слайд 7Показатель p = 2n – чётное натуральное число
0
х
у
у = х2,
у = х4 , у = х6, у = х8, …
у = х2n
Функция у=х2n чётная,
т.к. (–х)2n = х2n
График чётной функции
симметричен относительно
оси Оу.
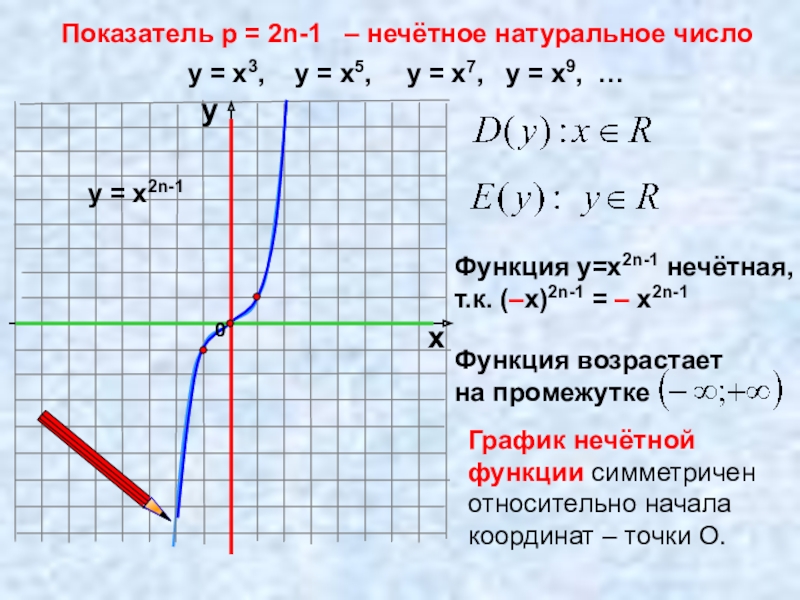
Слайд 9Показатель p = 2n-1 – нечётное натуральное число
х
у
у = х3,
у = х5, у = х7, у = х9, …
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
График нечётной функции симметричен относительно начала координат – точки О.
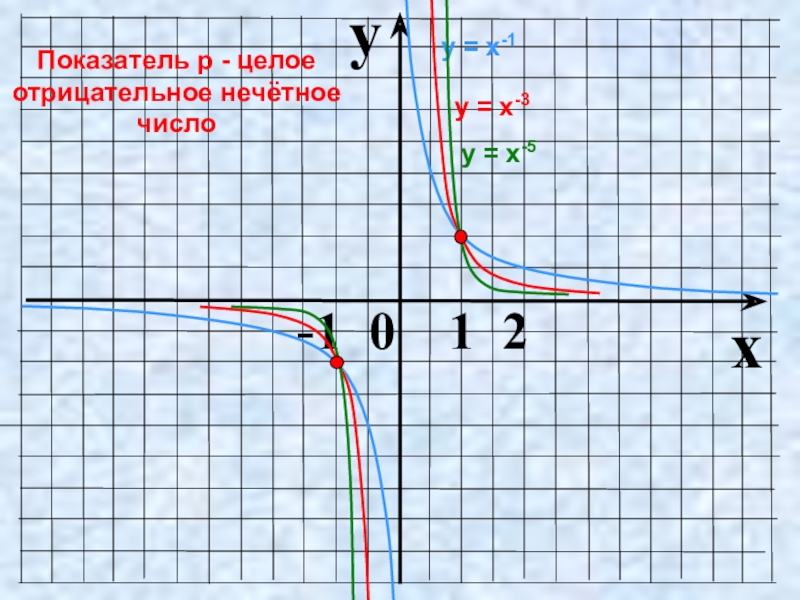
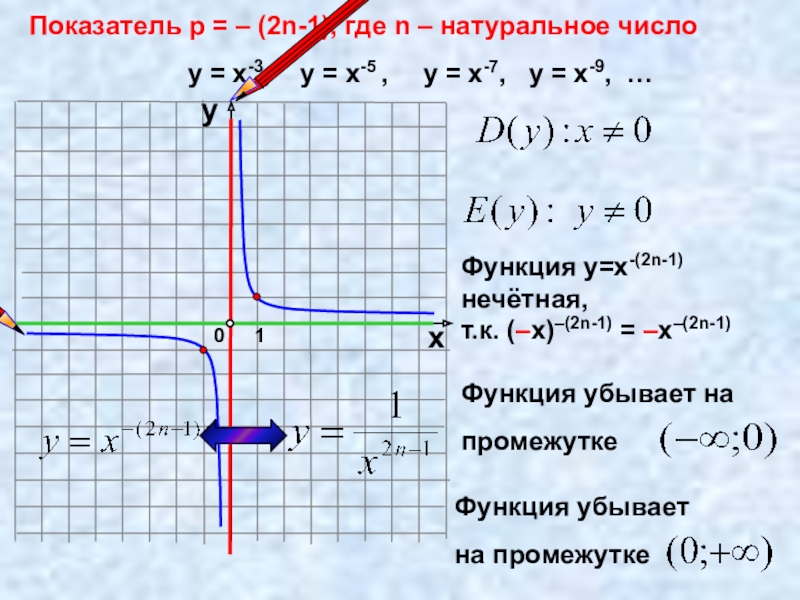
Слайд 11Показатель p = – (2n-1), где n – натуральное число
1
0
х
у
у =
х-3, у = х-5 , у = х-7, у = х-9, …
Функция у=х-(2n-1) нечётная,
т.к. (–х)–(2n-1) = –х–(2n-1)
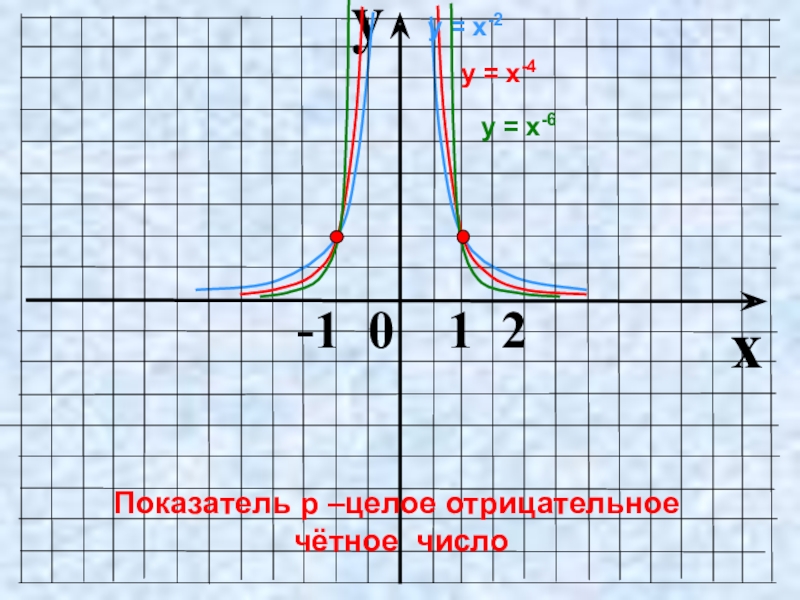
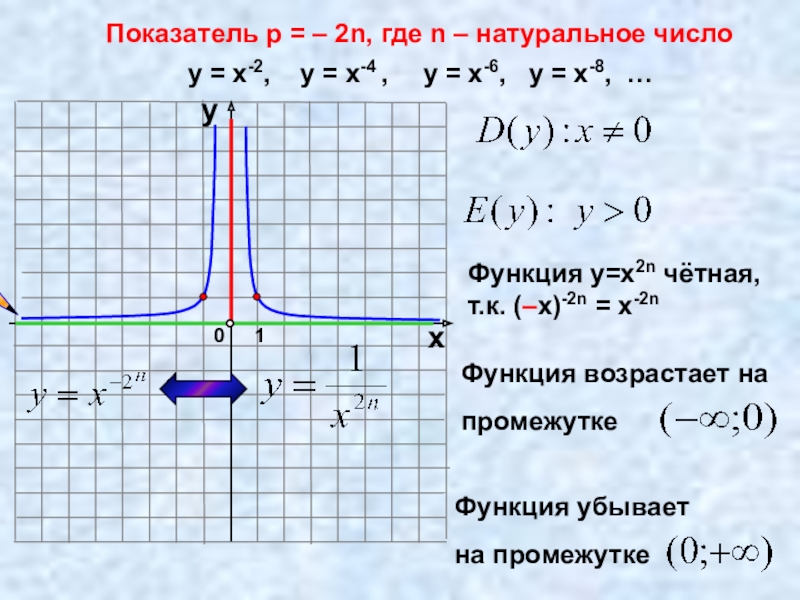
Слайд 13Показатель p = – 2n, где n – натуральное число
1
0
х
у
у =
х-2, у = х-4 , у = х-6, у = х-8, …
Функция у=х2n чётная,
т.к. (–х)-2n = х-2n
Слайд 20
Графическое лото (Работа в парах).
8
7
9
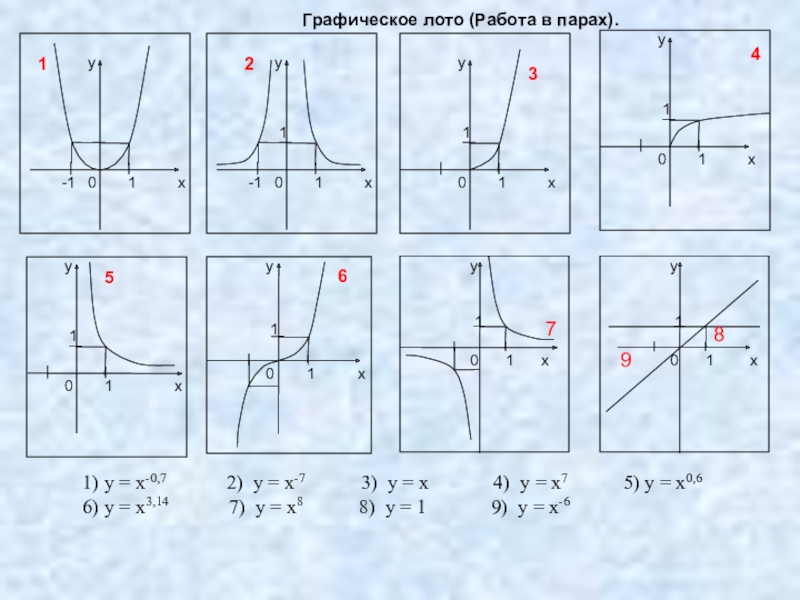
1) у = х-0,7 2) у = х-7 3) у = х 4) у = х7 5) у = х0,6
6) у = х3,14 7) у = х8 8) у = 1 9) у = х-6
Слайд 36-Для того, чтобы построить график данной функции, график исходной функции №
1 надо передвинуть вправо на 1 ед.отрезок, а затем вниз на 2 ед.отрезка.
Слайд 37
-Для того, чтобы построить график данной функции, график исходной функции №
4 надо передвинуть влево на 0.5 ед.отрезка, а затем вверх на 2 ед.отрезка.
Слайд 38-Для того, чтобы построить график данной функции, график исходной функции №
2 надо передвинуть вправо на 3 ед.отрезка, а затем вверх на 1,5 ед.отрезка.
Слайд 39-Для того, чтобы построить график данной функции, график исходной функции №
6 надо передвинуть вправо на 2 ед.отрезка, а затем вниз на 1 ед.отрезок.
Слайд 40-Для того, чтобы построить график данной функции, график исходной функции №
7 надо передвинуть влево на 2 ед.отрезка, а затем вниз на 2 ед.отрезка.
Слайд 41-Для того, чтобы построить график данной функции, график исходной функции №
7 надо передвинуть влево на 1 ед.отрезок, а затем вверх на 1,5 ед.отрезка.
Слайд 42-Для того, чтобы построить график данной функции, график исходной функции №
5 надо передвинуть влево на 1,5 ед.отрезка, а затем вниз на 1 ед.отрезок.
Слайд 43-Для того, чтобы построить график данной функции, график исходной функции №
3 надо передвинуть влево на 2 ед.отрезка, а затем вниз на 2 ед.отрезка.
Слайд 44-Для того, чтобы построить график данной функции, график исходной функции №
3 надо передвинуть влево на 1 ед.отрезок, а затем вверх на 1 ед.отрезок.
Слайд 51
Проверим свои знания:
Математический диктант с последующей взаимопроверкой.
Укажите область определения функции
у = х4
[ у = х 7 ].
2. Укажите область значений функции у = х 5
[ у = х 6].
3. Является ли функция у = х -3
[ у = х - 0,3 ] возрастающей ?
4. Изобразите схематически график функции у = х 2,3
[у = х 0,7].
5. Найдите область определения функции
у = ( х – 1 ) – 1 /2 [ у = (х + 2 ) – 1/3].
6. В одной системе координат постройте графики функций у = х 1/ 5 и у = х 7/5 [у = х ¼ и у = х 7/4 ].
[ у = х 7 ].
2. Укажите область значений функции у = х 5
[ у = х 6].
3. Является ли функция у = х -3
[ у = х - 0,3 ] возрастающей ?
4. Изобразите схематически график функции у = х 2,3
[у = х 0,7].
5. Найдите область определения функции
у = ( х – 1 ) – 1 /2 [ у = (х + 2 ) – 1/3].
6. В одной системе координат постройте графики функций у = х 1/ 5 и у = х 7/5 [у = х ¼ и у = х 7/4 ].
Слайд 53РЕФЛЕКСИЯ
Что вы ожидали от работы на данном уроке?
Сравните свои
предварительные цели и реально
достигнутые результаты.
Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным?
Что вам более всего удалось, какие моменты были выполнены наиболее успешно?
Перечислите в порядке убывания основные трудности, которые вы испытывали во время учебы. Как вы их преодолевали?
достигнутые результаты.
Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным?
Что вам более всего удалось, какие моменты были выполнены наиболее успешно?
Перечислите в порядке убывания основные трудности, которые вы испытывали во время учебы. Как вы их преодолевали?
Слайд 54Оцените свою работу на уроке
Напишите свою фамилию в тот столбик, на
какую оценку, по Вашему мнению, Вы работали.
