- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад па алгебре и началам математического анализа на тему: Логарифмические уравнения
Содержание
- 1. Презентация па алгебре и началам математического анализа на тему: Логарифмические уравнения
- 2. Цели урока: образовательная: обобщение знаний по теме
- 3. Что такое логарифмическое уравнение?Уравнение, содержащее неизвестное под
- 4. Основное логарифмическое тождество: Основное логарифмическое тождество —
- 5. Логарифм произведения положительных сомножителей равен сумме логарифмов
- 6. Упражнения Вычислить: log6 2 + log6 3 log124 + log12 36 log2 3 + log2 4/3
- 7. Решите уравнения
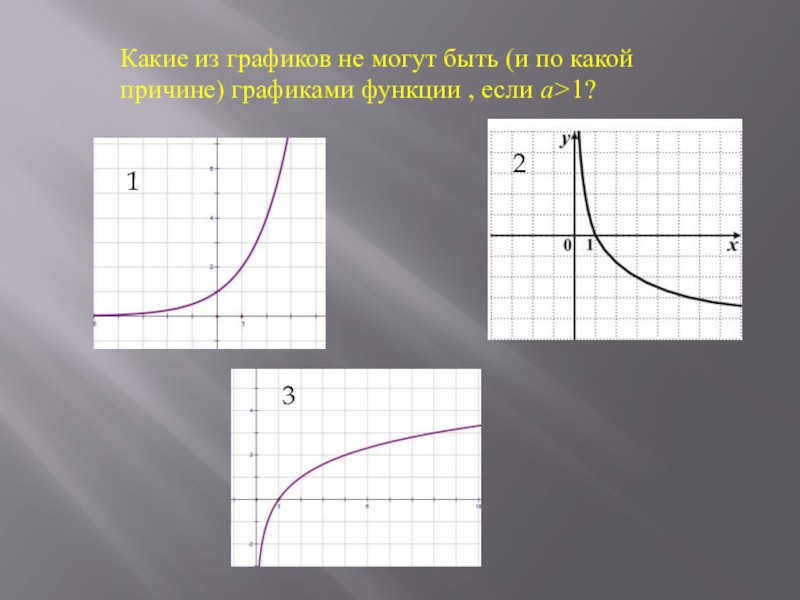
- 8. Какие из графиков не могут быть (и по какой причине) графиками функции , если a>1?123
- 9. Какие из функций возрастают, а какие убывают?
Слайд 2Цели урока:
образовательная: обобщение знаний по теме «Решение логарифмических уравнений»;
воспитательная:
развивающая: развитие самостоятельности, дифференцированного подхода к заданиям, умения принимать решения при выборе заданий.
Слайд 3Что такое логарифмическое уравнение?
Уравнение, содержащее неизвестное под знаком логарифма или (и)
Простейшим логарифмическим уравнением является уравнение вида:
loga x = b
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab.
Пример 1. Решить уравнения:
a) log2 x = 3, b) log3 x = -1
Слайд 4Основное логарифмическое тождество:
Основное логарифмическое тождество — это равенство
где
Например
Многие логарифмические выражения можно
Слайд 5Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:
loga N1·N2 = loga N1 + loga N2
Если N1·N2 > 0, тогда свойство примет вид
loga N1·N2 = loga |N1| + loga |N2| (a > 0, a ≠ 1, N1·N2 > 0)
Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:
loga N k = k loga N (a > 0, a ≠ 1, N > 0)
Если k - четное число (k = 2s), то
loga N 2s = 2s loga |N| (a > 0, a ≠ 1, N ≠ 0).
Иногда оказывается полезным от логарифмов по одному основанию (например, а) перейти к логарифмам по другому основанию (например, с). В этом случае пользуются следующей формулой:
Слайд 6Упражнения
Вычислить:
log6 2 + log6 3 log124 + log12 36
log2 3 + log2 4/3 log5 100 — log5 4
log3 7
log10 40 + log10 25 log6 1/18 + log6 1/12
log10 0,18 — log10 180 log0,1 50 — log0,1 0,5