- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке
Содержание
- 1. Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке
- 2. Функция у = f(х) определена на отрезке
- 3. Функция у = f(х) определена на отрезке
- 4. Функция у = f(х) определена на отрезке
- 5. 1. Найти наибольшее значение функции по её
- 6. 2. Найти наименьшее значение функции по её
- 7. Найти наибольшее и наименьшее значения функции по её графику
- 8. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
- 9. ° ВЫВЕСТИ АЛГОРИТМ НАХОЖДЕНИЯ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО
- 10. Если функция f(x) возрастает (убывает) на [a;b],
- 11. Если функция у = f(х) на
- 12. Наибольшего (наименьшего) значения непрерывная на [а; b]
- 13. Проанализируйте все рассмотренные случаи. В каких точках функция достигает наибольшего (наименьшего) значений?
- 14. Выводы 1.Если
- 15. Алгоритм нахождения наибольшего и наименьшего значений непрерывной
- 16. Найдите наименьшее значение функции y = x3
- 17. Найдите наименьшее значение функции y = x3
- 18. Найдем критические точки, которые принадлежат заданному отрезку.Выбрать
- 19. Найдите наибольшее значение функции на отрезке [
- 20. Найдите наибольшее значение
- 21. Функция на всей области определения убывает. Нетрудно
- 22. Найдите наибольшее значение
- 23. Нахождение наибольшего и наименьшего значений функции
- 24. Рекламный щит имеет форму прямоугольника S=9 м2. Изготовьте щит в виде прямоугольника с наименьшим периметром
- 25. Из всех прямоугольников с площадью 9м2,найти прямоугольник,
- 26. Найдем наименьшее значение по известному алгоритмуОтвет: шит имеет форму квадрата со стороной 3м
- 27. Задача 2. Кусок проволоки 48 метров сгибают
- 28. Решение: Пусть длина- а см. ширина –в
- 29. Рефлексия. 1.Каковы ваши главные результаты, что вы
- 30. Домашнее заданиеУровень «А»: № 938 , № 940Уровень «В»: № 944Уровень «С»: № 947
- 31. СПАСИБО ЗА УРОК
Слайд 1« В мире не происходит ничего,
в чем бы ни был
какого-нибудь максимума или минимума!»
Леонард Эйлер
Слайд 2
Функция у = f(х) определена на отрезке [-6;3]. График её производной
Слайд 3
Функция у = f(х) определена на отрезке [-5;4]. График её производной
Слайд 4
Функция у = f(х) определена на отрезке [-5;4]. График её производной
Слайд 51. Найти наибольшее значение функции по её графику
5
4
2
-5
у наиб. = 4
[-5; 6]
у наиб. = 5
[-7; 6]
1
1
Слайд 62. Найти наименьшее значение функции по её графику
у наим. =- 3
[-7; 4]
у наим. = -4
[-7; 6]
-3
-2
4
-4
Слайд 9° ВЫВЕСТИ АЛГОРИТМ НАХОЖДЕНИЯ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ. °
Цели урока:
Слайд 10
Если функция f(x) возрастает (убывает) на [a;b], то наибольшего или наименьшего
Слайд 11
Если функция у = f(х) на отрезке [а; b] имеет
fmax = fнаиб. fmin = fнаим.
Слайд 12
Наибольшего (наименьшего) значения непрерывная на [а; b] функция достигает либо на
Слайд 13
Проанализируйте все рассмотренные случаи. В каких точках функция достигает наибольшего (наименьшего)
Слайд 14
Выводы
1.Если функция непрерывна на отрезке, то она достигает на нем и
2.Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3.Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в критической точке.
Слайд 15Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x)
1. Найти производную f´(х)
2. Найти критические точки функции, лежащие внутри oтрезка [a;b]
3. Вычислить значение функции у= f(x) в точках,
отобранных на втором шаге, и в точках a и b.
Выбрать среди этих значений наименьшее
( это будет унаим )и наибольшее (это будет унаиб )
Слайд 16Найдите наименьшее значение функции
y = x3 – 27x на отрезке
1) y / = 3x2 – 27
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3) y(0) = 0
Выполнение этапов решения можно изменить, как вам удобно.
Слайд 17Найдите наименьшее значение функции
y = x3 – 27x на отрезке
1) y / = 3x2 – 27
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3)
Другой способ решения
min
Наименьшее значение функция будет принимать в точке минимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в концах отрезка будет сложным.
Слайд 18Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из полученных значений.
1) y(0) = 4
2) y / = 3x2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
2.
Слайд 19Найдите наибольшее значение функции
на отрезке [ 3; 10 ]
3.
Найдем критические
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
1). Первое число меньше 1, т.к. знаменатель e4 > 5.
2). Второе число – отрицательноe.
3). Значит, наибольшее число 1.
1
Слайд 20 Найдите наибольшее значение функции
4.
max
Наибольшее значение функция будет принимать в точке максимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
y = 5ln(x+5) – 5x
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках
и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее или наибольшее.
0
Можно рассуждать иначе
Запишем функцию в удобном для дифференцирования виде
Слайд 21Функция на всей области определения убывает. Нетрудно догадаться, что у /
Тогда наименьшее значение функция будет иметь в правом конце отрезка, т.е. в точке х=0.
Найдите наименьшее значение функции
y = 5cosx – 6x + 4 на отрезке
5.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
1
0
Если вы не догадались, то вычислите значения функции в каждом конце отрезка и выберите наименьшее.
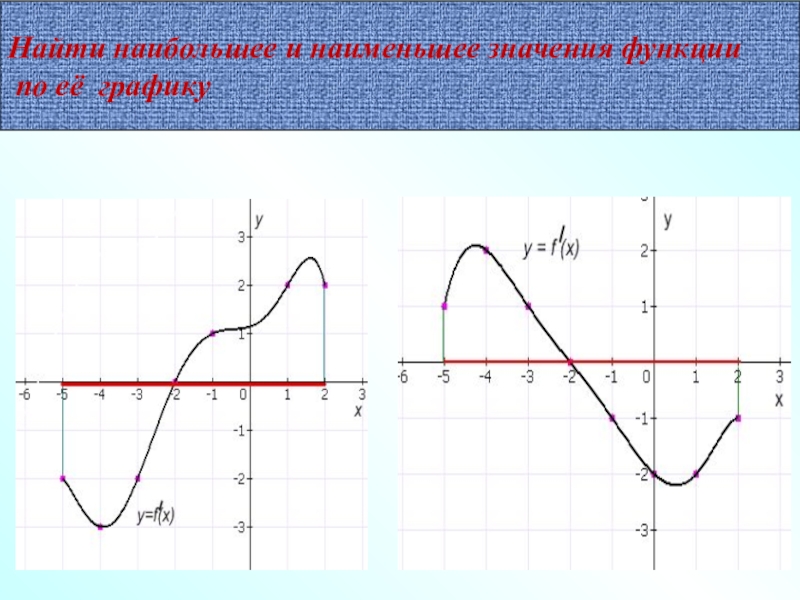
Слайд 22 Найдите наибольшее значение функции
6.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
-1
0
Слайд 23 Нахождение наибольшего и наименьшего значений функции широко применяется при решении
ПРИМЕР. Рекламный щит имеет форму прямоугольника S=9 м2. Изготовьте щит в виде прямоугольника с наименьшим периметром
Слайд 24Рекламный щит имеет форму прямоугольника S=9 м2. Изготовьте щит в виде
Слайд 25Из всех прямоугольников с площадью 9м2,найти прямоугольник, периметр которого наименьший.
1.S= a*b
х - ширина прямоугольника
9./х – длина прямоугольника
Р= ( х+9/х) * 2
2.
3. Рассмотрим функцию у=( х+9/х) * 2
х>0
Слайд 26Найдем наименьшее значение по известному алгоритму
Ответ: шит имеет форму квадрата со
Слайд 27Задача 2
. Кусок проволоки 48 метров сгибают так, чтобы получился прямоугольник.
Слайд 28Решение: Пусть длина- а см. ширина –в см. Тогда периметр 2(а+в)
Находим значения функции при х=0 х=12 и х=48 ( на концах промежутка 0,48) f(0)=0 f(12)=144 f(48)= -1152: площадь будет наибольшей , если стороны равны по 12 см данный прямоугольник -квадрат.
Слайд 29Рефлексия.
1.Каковы ваши главные результаты, что вы поняли, чему научились?
2.Способы,
3.Какие чувства испытывали во время урока?
4.Пережили ли вы чувство радости, успеха?
5.С каким настроением вы уходите с урока?

![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Функция у = f(х) определена на отрезке [-6;3]. График её производной Функция у = f(х) определена на отрезке [-6;3]. График её производной изображен на рисунке. Определите промежутки возрастания](/img/thumbs/5f46bb1f22956638c8b11f4e57aaac5a-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Функция у = f(х) определена на отрезке [-5;4]. График её производной Функция у = f(х) определена на отрезке [-5;4]. График её производной изображен на рисунке. Определите точки максимума](/img/thumbs/328f27b139c6a800668616f938439093-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Функция у = f(х) определена на отрезке [-5;4]. График её производной Функция у = f(х) определена на отрезке [-5;4]. График её производной изображен на рисунке. Определите сколько существует](/img/thumbs/a779029cf4fbc3dce4ebd371e76dc6dc-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке 1. Найти наибольшее значение функции по её графику 1. Найти наибольшее значение функции по её графику на [ -5;6]](/img/thumbs/3d0d5c9e2a3c2d697d302c9bb735412b-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке 2. Найти наименьшее значение функции по её графику на 2. Найти наименьшее значение функции по её графику на [ -7;4] и](/img/thumbs/bc7216a691677f34fa69b8b51618b9c0-800x.jpg)


![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Если функция f(x) возрастает (убывает) на [a;b], то наибольшего или наименьшего Если функция f(x) возрастает (убывает) на [a;b], то наибольшего или наименьшего значения она достигает на концах этого](/img/thumbs/5eeb29aff8cd1f374798165062f2a67a-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Если функция у = f(х) на отрезке [а; b] имеет Если функция у = f(х) на отрезке [а; b] имеет лишь одну критическую точку и она](/img/thumbs/e3af3cea5ad8e4821ebb31dd6a37ef20-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Наибольшего (наименьшего) значения непрерывная на [а; b] функция достигает либо на Наибольшего (наименьшего) значения непрерывная на [а; b] функция достигает либо на концах отрезка, либо в критических точках,](/img/thumbs/de28abee86b15b7cbb33bafebd511daa-800x.jpg)

![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) на отрезке [a;b]1. Найти производную](/img/thumbs/65c736d18a04492d54753e1ebfa8f7bb-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Найдите наименьшее значение функции y = x3 – 27x на отрезке Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]1) y / = 3x2](/img/thumbs/71662fbcca9feec51dd3e4264194217f-800x.jpg)
![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Найдите наименьшее значение функции y = x3 – 27x на отрезке Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]1) y / = 3x2](/img/thumbs/58d87af934103beb2b423a660daf9dfc-800x.jpg)

![Презентация открытого урока по алгебре и началам анализа на тему Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке Найдите наибольшее значение функции на отрезке [ 3; 10 ]3.Найдем критические Найдите наибольшее значение функции на отрезке [ 3; 10 ]3.Найдем критические точки, которые принадлежат заданному отрезку.Выбрать наибольшее](/img/thumbs/c6dffb69fde1cdf17ff726f4444834d6-800x.jpg)