- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Некоторые интересные приемы быстрого счета
Содержание
- 1. Презентация Некоторые интересные приемы быстрого счета
- 2. «Кто с детских лет занимается математикой,
- 3. АктуальностьБыстрый счет помогает людям в повседневной жизни,
- 4. СТАРИННЫЕ СПОСОБЫ УМНОЖЕНИЯ
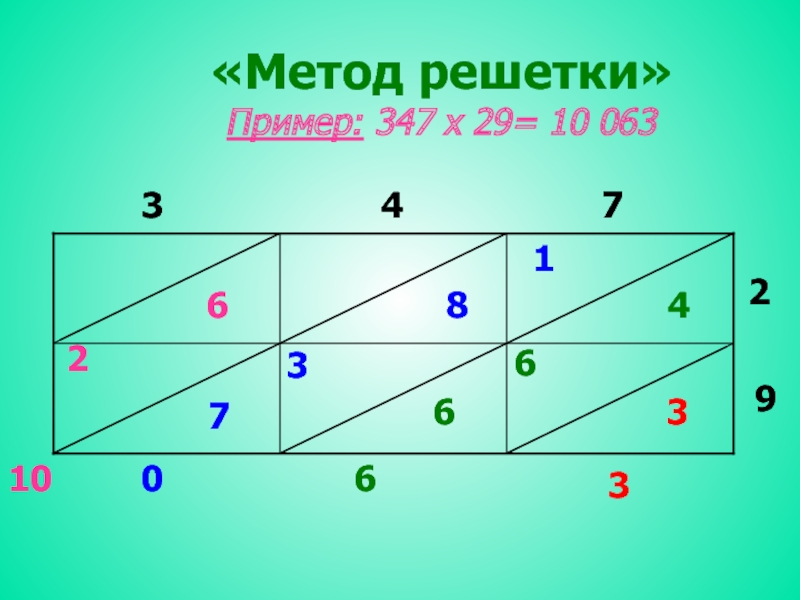
- 5. «Метод решетки» Пример: 347 х 29= 10 06334729681427366336010
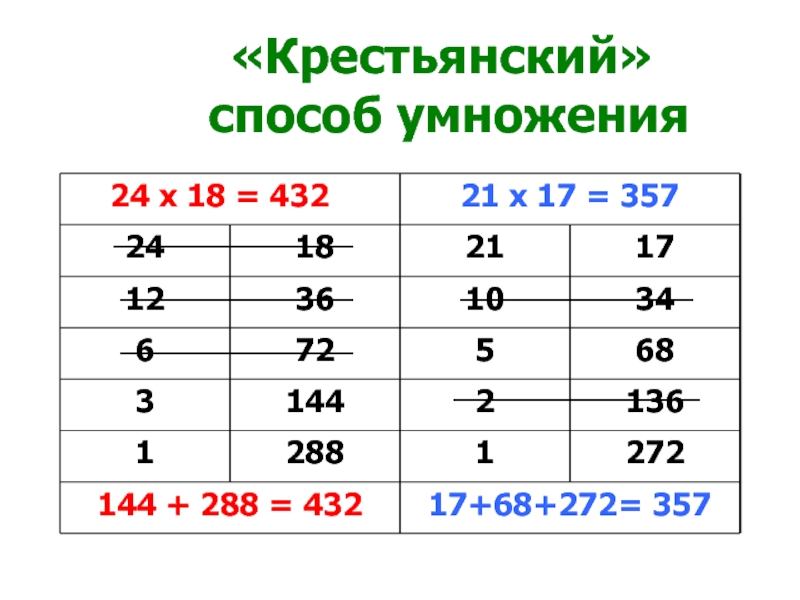
- 6. «Крестьянский» способ умножения
- 7. Признаки делимостиЭти признаки нам хорошо знакомы.Признак делимости
- 8. Признак делимости на 4 Число делится на
- 9. Признак делимости на 8 Число делится на
- 10. Признак делимости на 11 На 11 делятся только
- 11. Некоторые способы быстрых вычислений
- 12. Умножение чисел, у которых число десятков одинаково,
- 13. Умножение двузначных чисел, у которых сумма цифр
- 14. Умножение на 11 При умножении числа не 11
- 15. 58х11=638 а) пишем 8
- 16. Умножение двузначных чисел на 101, трехзначных –
- 17. Возведение в квадрат двузначных чисел, имеющих 5
- 18. Возведение в квадрат числа, оканчивающегося на "5"
- 19. Возведение в квадрат числа методом «Обратной пирамиды»67
- 20. Некоторые удивительные случаи действий над числами 12345679
- 21. 0 х 9+1= 11 х 9+2 =
- 22. 11 х 11=121111 х 111=123211111 х 1111=123432111111
- 23. Подводя итоги… Уверена, что
Слайд 2 «Кто с детских лет
занимается математикой,
тот развивает внимание,
тренирует
воспитывает настойчивость
и упорство в достижении цели».
А. Маркушевич
Слайд 3Актуальность
Быстрый счет помогает людям в повседневной жизни, а ученикам на «отлично»
Цель исследования:
Выявить и изучить методы и приемы устного счета для их практического применения при выполнении арифметических действий без использования счетных машин;
доказать необходимость умения быстро считать.
Слайд 7Признаки делимости
Эти
признаки нам
хорошо
знакомы.
Признак делимости на 2;
Признак делимости на
и на 9;
Признак делимости на 5;
Признак делимости
на 10,100 и 1000.
Слайд 8Признак делимости на 4
Число делится на 4, если две последние
его цифры
делящееся на 4. В остальных случаях
число на 4 не делится.
31700 делится на 4, так как оканчивается двумя нулями;
215634 не делится на 4, так как последние две цифры
дают число 34, не делящееся на 4;
16628 делится на 4, так как две последние цифры
дают число 28, делящееся на 4.
Слайд 9Признак делимости на 8
Число делится на 8, если три последних цифры
120000 делится на 8 (три нуля в конце);
170004 не делится на 8 (три последние цифры дают число 4, не делящееся на 8);
111072 делится на 8 (три последние цифры дают число 72, делящееся на 8).
Слайд 10Признак делимости на 11
На 11 делятся только те числа, у которых
Число 103785 делится на 11, так как сумма цифр, занимающих нечетные места, 1+3+8=12 равна сумме цифр, занимающих четные места 0+7+5=12.
Число 9163627 делится на 11, так как сумма цифр, занимающих нечетные места, есть 9+6+6+7=28,а сумма цифр, занимающих четные места, есть 1+3+2=6; разность между числами 28 и 6 есть 22, а это число делится на 11.
Слайд 12Умножение чисел, у которых число десятков одинаково,
а сумма единиц равна 10
При
13 х 17 = 221
а)1 х 2 =2, пишем 2
б)3 х 7 = 21
приписываем справа 21
38 Х 32 = 1216
а)3 х 4 = 12, пишем 12
б)8 х 2 = 16
приписываем справа 16
Слайд 13Умножение двузначных чисел, у которых сумма цифр десятков равна 10, а цифры
При умножении двузначных чисел, у которых
сумма цифр десятков равна 10, а цифры единиц
одинаковые, надо:
перемножить цифры десятков и прибавить к
результату цифру единиц,
к полученному результату приписать произведение
единиц так, чтобы получилось четырехзначное число.
Примеры:
72 × 32 = 2304; 7 × 3 + 2 = 23; 2 × 2 = 04
67 × 47 = 3149; 6 × 4 + 7 = 31; 7 × 7 = 49
Слайд 14Умножение на 11
При умножении числа не 11 необходимо записать последнюю цифру
Слайд 15 58х11=638
а) пишем 8
б) 5+8=13, пишем 3,1 помним
в) 5+1=6, пишем 6
3765х11=41415
а) пишем 5
б)5+6=11, пишем1, 1 помним
в)7+6+1=14, пишем 4, 1 помним
г)3+7+1=11, пишем1, 1 помним
д)3+1=4, пишем 4
Слайд 16Умножение двузначных чисел на 101,
трехзначных – на 1001
Чтобы двузначное число умножить
Примеры: 32 × 101 = 3232;
56 × 101 = 5656.
Чтобы трехзначное число умножить на 1001, надо к этому числу справа приписать это же число.
Примеры: 324 × 1001 = 324324;
Слайд 17Возведение в квадрат двузначных чисел, имеющих 5 десятков
Чтобы возвести в квадрат
Пример:
а) 25+1=26, пишем 26;
б) , приписываем 01;
Слайд 18Возведение в квадрат числа, оканчивающегося на "5"
Следует число, получаемое из данного
75 х 75 = 5625
(7 х 8 = 56, дописываем 25);
105 х 105 = 11025
(10 х 11=110, дописываем 25)
Слайд 19Возведение в квадрат числа методом «Обратной пирамиды»
67 * 67 = 4489
3 6 4 9
8 4
Результат: 4 4 8 9
Слайд 20Некоторые удивительные случаи действий над числами
12345679 х 9 =
12345679 х 18 = 222 222 222
12345679 х 27 = 333 333 333 12345679 х 36 = 444 444 444 12345679 х 45 = 555 555 555 12345679 х 54 = 666 666 666 12345679 х 63 = 777 777 777
12345679 х 72 = 888 888 888 12345679 х 81 = 999 999 999
Слайд 210 х 9+1= 1
1 х 9+2 = 11
12 х 9+3 =
123 х 9+4 = 1111
1234 х 9+5 = 11111
12345 х 9+6 = 111111
123456 х 9+7 = 1111111
1234567 х 9+8 = 11111111
12345678 х 9+9 = 111111111
123456789 х 9+10 = 1.111.111.111
Слайд 2211 х 11=121
111 х 111=12321
1111 х 1111=1234321
11111 х 11111=123454321
111111 х 111111=12345654321
1111111
11111111 х 11111111=123456787654321
111111111 х 111111111=12345678987654321