- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Наибольшее и наименьшее значения функции , 10 класс.
Содержание
- 1. Презентация: Наибольшее и наименьшее значения функции , 10 класс.
- 2. 1. Найти наибольшее значение функции по её
- 3. 2. Найти наименьшее значение функции по её
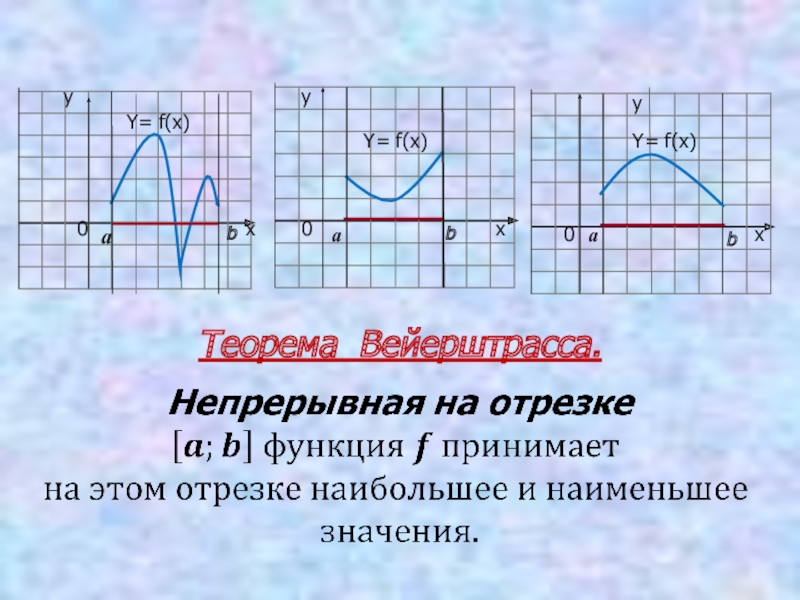
- 4. yyxx000аааbbbY= f(x)Y= f(x)Y= f(x)Теорема Вейерштрасса.
- 5. Алгоритм нахождения наибольшего и наименьшего значений непрерывной
- 6. Обозначение.
- 7. Найти наибольшее и наименьшее значение функции у
- 8. Найти наибольшее и наименьшее значение функции у
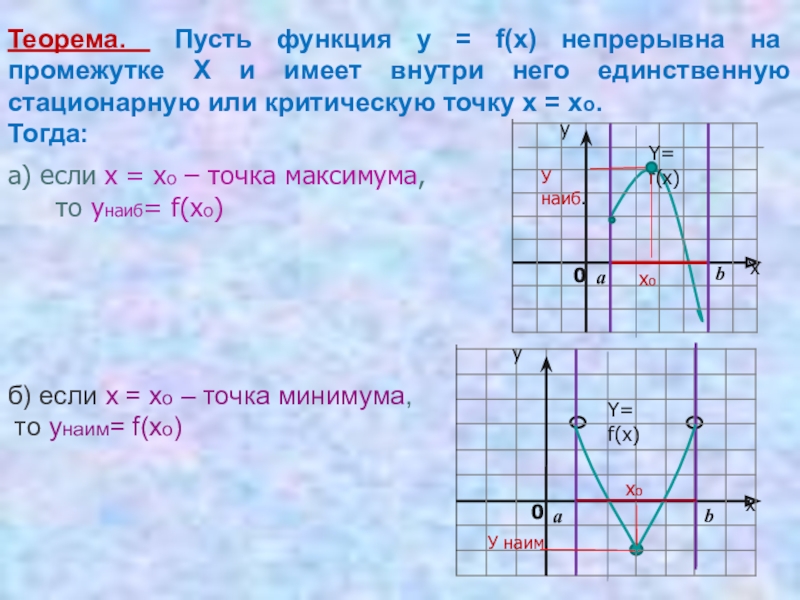
- 9. а) если х = хо – точка
Слайд 21. Найти наибольшее значение функции по её графику
5
4
2
-5
у наиб. = 4
[-5; 6]
у наиб. = 5
[-7; 6]
1
1
Слайд 32. Найти наименьшее значение функции по её графику
у наим. =- 3
[-7; 4]
у наим. = -4
[-7; 6]
-3
-2
4
-4
Слайд 5Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x)
1. Найти производную f´(х);
2. Найти точки, в которых f´(х)=0 или f´(х) не существует, и отобрать из них те, что лежат внутри oтрезка [a;b];
3. Вычислить значение функции на концах отрезка и в выбранных критических точках. Выбрать из полученных чисел наибольшее и наименьшее значения.
Слайд 7
Найти наибольшее и наименьшее значение функции у = х³ - 3х²
без построения графика.
Задание 1.
Слайд 8
Найти наибольшее и наименьшее значение функции у = х³ - 5х²
без построения графика.
Задание 2.
Ответ: : у наим = у (-1) = -13; у наиб = у(1) = 3
Слайд 9а) если х = хо – точка максимума,
то унаиб= f(xo)
Теорема.
Тогда:
б) если х = хо – точка минимума,
то унаим= f(xo)

![Презентация: Наибольшее и наименьшее значения функции , 10 класс. 1. Найти наибольшее значение функции по её графику 1. Найти наибольшее значение функции по её графику на [ -5;6]](/img/thumbs/6eb4031e607850f8b1646d6514930005-800x.jpg)
![Презентация: Наибольшее и наименьшее значения функции , 10 класс. 2. Найти наименьшее значение функции по её графику на 2. Найти наименьшее значение функции по её графику на [ -7;4] и](/img/thumbs/e4fb0bcac87dd426824e17dda4936387-800x.jpg)
![Презентация: Наибольшее и наименьшее значения функции , 10 класс. Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) на отрезке [a;b]1. Найти производную](/img/thumbs/e7f0380b89449003a32a03cd45723372-800x.jpg)


![Презентация: Наибольшее и наименьшее значения функции , 10 класс. Найти наибольшее и наименьшее значение функции у = х³ - 5х² Найти наибольшее и наименьшее значение функции у = х³ - 5х² + 7х на [-1; 2] без](/img/thumbs/41943d85baed01c69fd94020eea67a51-800x.jpg)