ctgt ≥a, ctgt
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Метод интервалов при решении тригонометрических неравенств (10 класс).
Содержание
- 1. Презентация. Метод интервалов при решении тригонометрических неравенств (10 класс).
- 2. Неравенство cost ≤ a0xy1. Отметить на оси
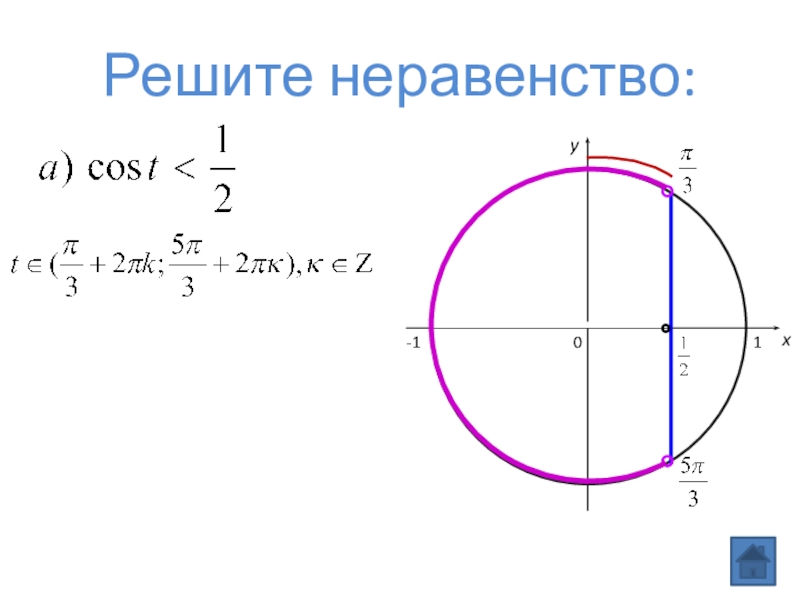
- 3. 0xy-11Решите неравенство:
- 4. Неравенство sint > a0xy1. Отметить на оси
- 5. Пример. Решите неравенство sin(2x–3)>–0,5.---
- 6. 0xyat1-11Неравенство tg t > a1. Отметить на
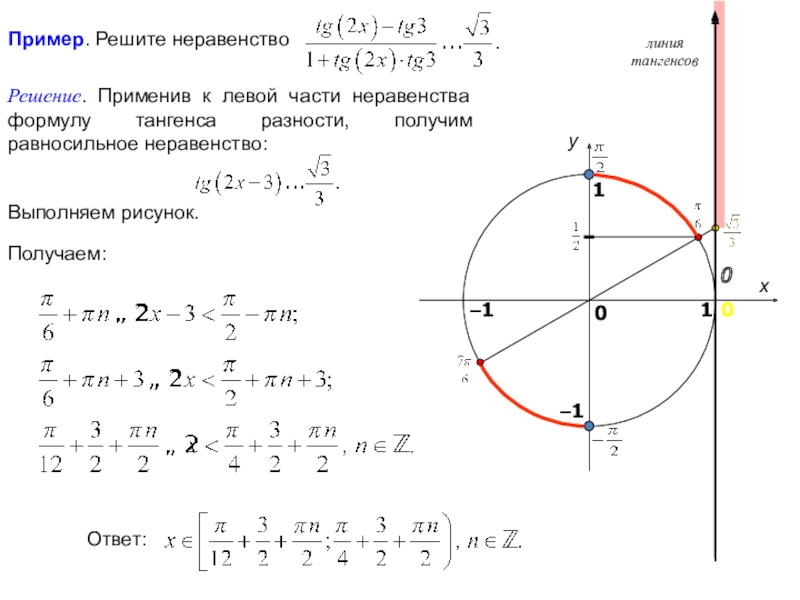
- 7. Пример. Решите неравенство xy101–10линия тангенсов–10Получаем:
- 8. Методы решений тригонометрических неравенств: метод введения новой переменной; метод интервалов.
- 9. Алгоритм решения тригонометрических неравенств методом интервалов.С помощью преобразований привести неравенство к виду f(t)>0 (f(t)
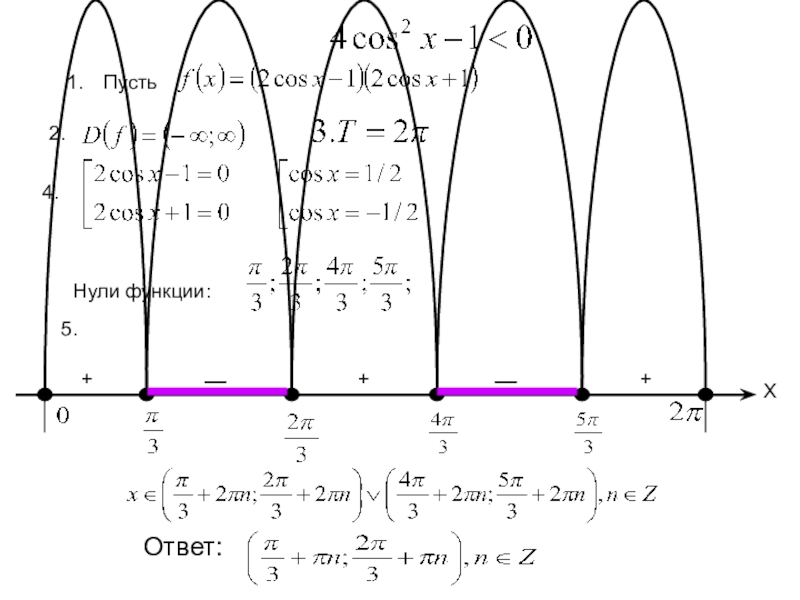
- 10. 2.5. Нули функции:Ответ:
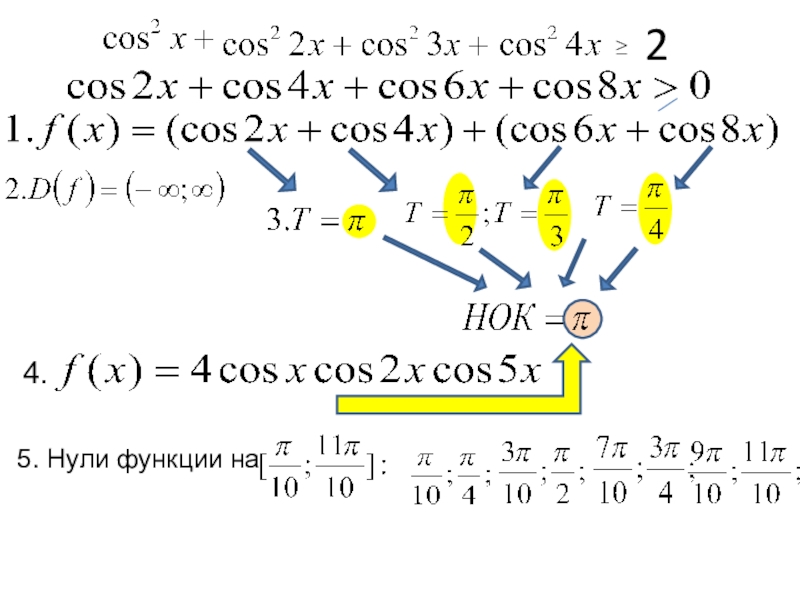
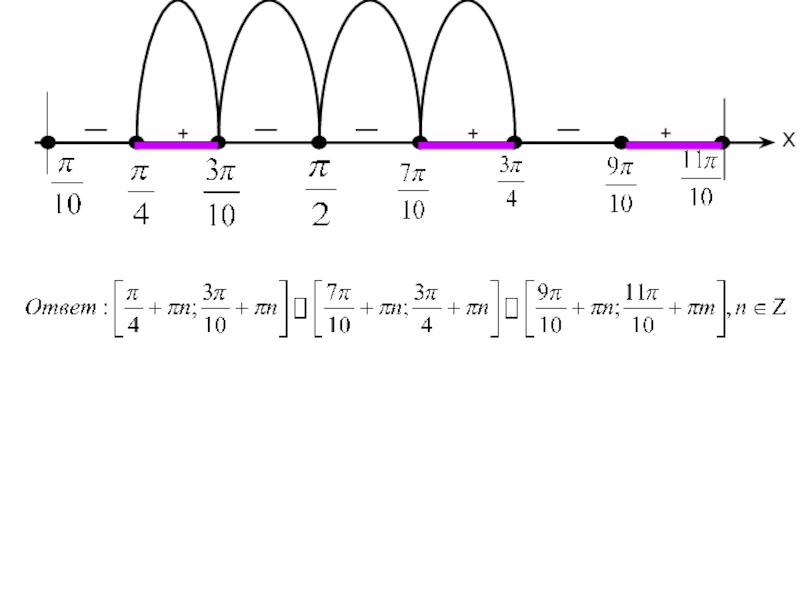
- 11. ≥25. Нули функции на 4.
- 12. Слайд 12
- 13. Спасибо за внимание!
Неравенство cost ≤ a0xy1. Отметить на оси абсцисс промежуток x ≤ a.2. Выделить дугу окружности, соответствующую промежутку. 3. Записать числовые значения граничных точек дуги.4. Записать общее решение неравенства.at12π-t1-11
Слайд 1Тригонометрические
неравенства
cost >a, cost ≤ a
sint >a, sint ≤ a
tgt
≤ a, tgt >a
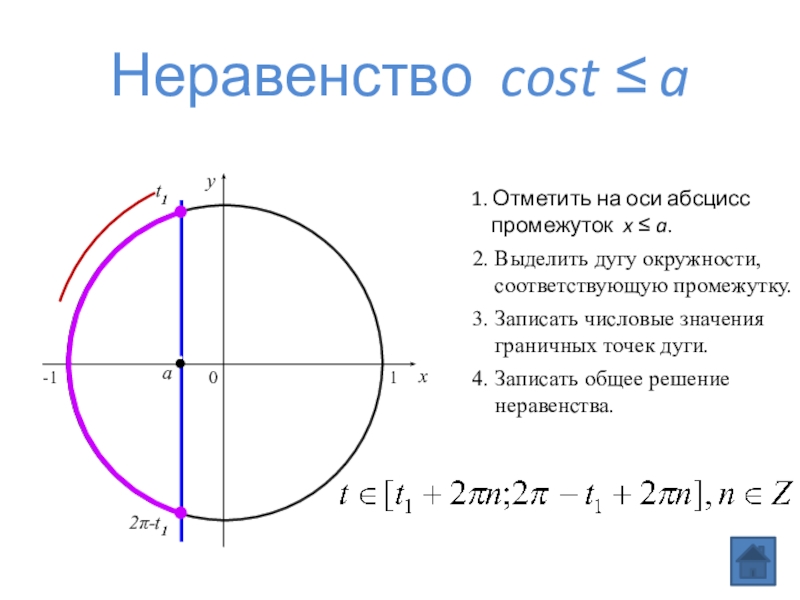
Слайд 2Неравенство cost ≤ a
0
x
y
1. Отметить на оси абсцисс
промежуток x
≤ a.
2. Выделить дугу окружности,
соответствующую промежутку.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
a
t1
2π-t1
-1
1
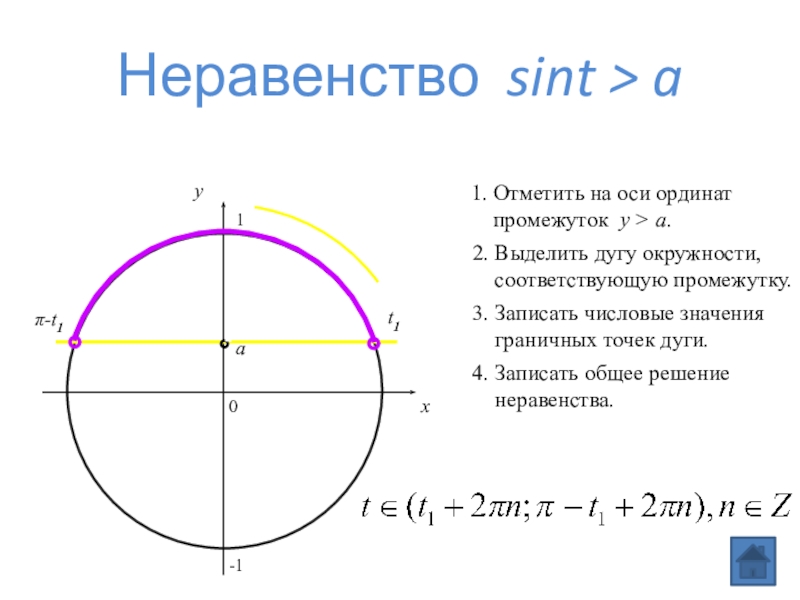
Слайд 4Неравенство sint > a
0
x
y
1. Отметить на оси ординат
промежуток y
> a.
2. Выделить дугу окружности,
соответствующую промежутку.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
a
t1
π-t1
-1
1
Слайд 6
0
x
y
a
t1
-1
1
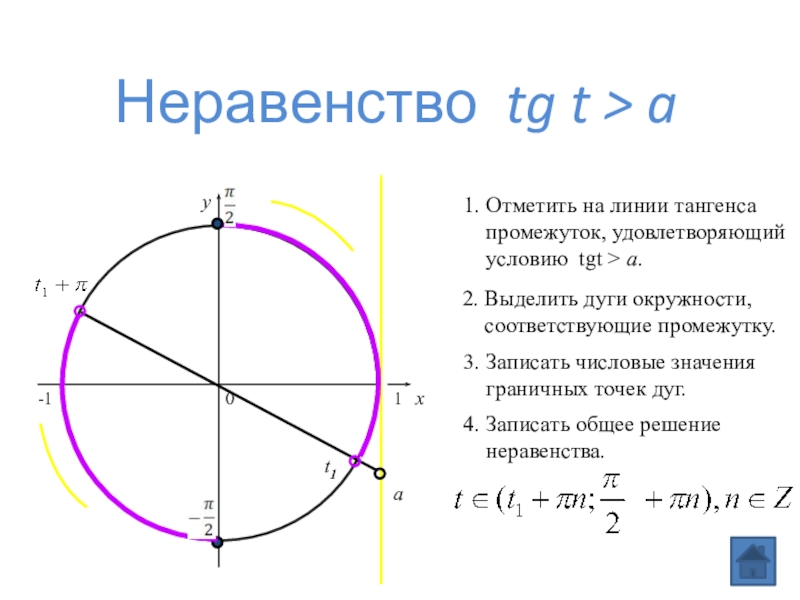
Неравенство tg t > a
1. Отметить на линии тангенса
промежуток,
удовлетворяющий
условию tgt > a.
условию tgt > a.
2. Выделить дуги окружности,
соответствующие промежутку.
3. Записать числовые значения
граничных точек дуг.
4. Записать общее решение
неравенства.
Слайд 8
Методы решений тригонометрических неравенств:
метод введения новой переменной;
метод интервалов.
Слайд 9Алгоритм решения тригонометрических неравенств методом интервалов.
С помощью преобразований привести неравенство к
виду f(t)>0 (f(t)<0) .
Найти основной период Т функции f (Т равен НОК периодов, входящих в неравенство тригонометрических функций).
Найти нули функции f(t) на промежутке , решив уравнение f(t)=0.
Найти точки разрыва функции f(t) на этом промежутке.
Найденными точками разделить отрезок на части, в каждой из которых функция f(t) имеет постоянный знак.
Определить знак функции в каждой части методом пробных точек (результат удобно оформить в виде таблицы).
Выбрать те части, в которых выполняется исходное неравенство.
Учитывая периодичность функции, записать решение исходного неравенства.
Найти основной период Т функции f (Т равен НОК периодов, входящих в неравенство тригонометрических функций).
Найти нули функции f(t) на промежутке , решив уравнение f(t)=0.
Найти точки разрыва функции f(t) на этом промежутке.
Найденными точками разделить отрезок на части, в каждой из которых функция f(t) имеет постоянный знак.
Определить знак функции в каждой части методом пробных точек (результат удобно оформить в виде таблицы).
Выбрать те части, в которых выполняется исходное неравенство.
Учитывая периодичность функции, записать решение исходного неравенства.
