- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад материала по теме: Методы решения рациональных неравенств
Содержание
- 1. Презентация материала по теме: Методы решения рациональных неравенств
- 2. Свойства равносильных неравенств.
- 3. Свойство 1. Если к обеим частям неравенства
- 4. Свойство 2. Если в неравенстве любое слагаемое,
- 5. Свойство 3. Если обе части неравенства умножить
- 6. Свойство 4. Если обе части неравенства умножить
- 7. Метод интервалов.
- 8. х4 + 3х3 – 4х > 0. Пример: Решить неравенство
- 9. Разложим на множители многочлен Р4(х), стоящий в
- 10. Рассмотрим функцию у= х(х-1)(х+2)2Область определения
- 11. Дробно – рациональные неравенства.
- 12. Пример: Решить неравенство (х+2) / (х2-х-2)< -1.
- 13. Решение: Прибавляя к обеим частям неравенства
- 14. Неравенства, содержащие неизвестное под знаком абсолютной величины.
- 15. Пример: Решить неравенство ⏐х2 - 2⏐
- 16. Предположим, что х2–2≥0,тогда неравенство принимает вид х2+х–2
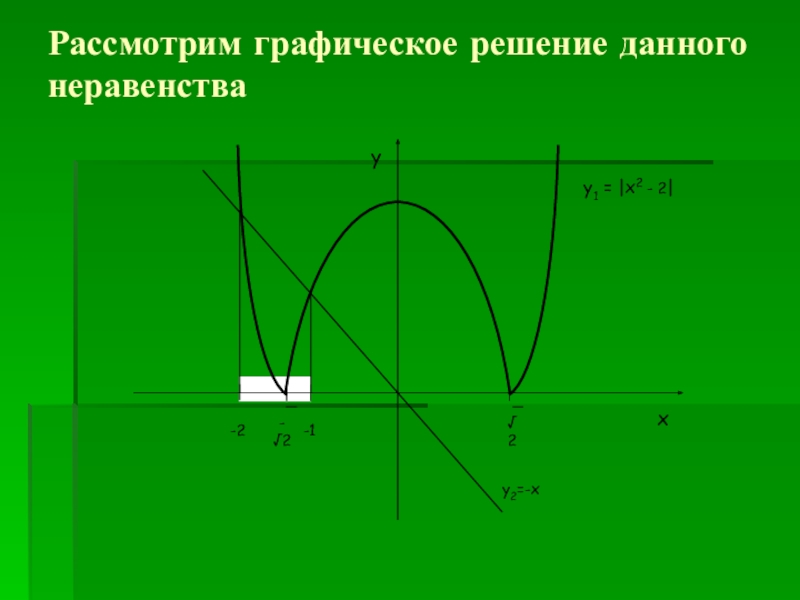
- 17. Рассмотрим графическое решение данного неравенства
- 18. Неравенства с параметрами.
- 19. Неравенства с параметрами.Пример: Для всех значений а
- 20. Приведем графическую иллюстрацию решения этого примера. а
- 21. Графическое решение неравенств.
- 22. Графическое решение неравенств.Пример. Решить графически систему неравенств
Слайд 1Презентация материала по теме:
Методы решения рациональных неравенств.
Выполнила: преподаватель математики Лупилина Н.В.
Слайд 3Свойство 1.
Если к обеим частям неравенства прибавить одно и тоже
Слайд 4Свойство 2.
Если в неравенстве любое слагаемое, которое имеет смысл при
Слайд 5Свойство 3.
Если обе части неравенства умножить на одно и то
Слайд 6Свойство 4.
Если обе части неравенства умножить на одно и то
Слайд 9Разложим на множители многочлен Р4(х), стоящий в левой части неравенства. Вынося
Решение. Разложим на множители многочлен Р4(х), стоящий в левой части неравенства (*). Вынося множитель х за скобку, получаем
Р4(х) = х(х3 + 3х2 – 4).
Второй сомножитель, представляющий собой кубический многочлен, имеет корень х = 1. Следовательно, он может быть представлен в виде
х3 + 3х2 – 4 = (х-1)(х2 + 4х + 4) = (х-1)(х + 2) 2.
Таким образом, Р4(х) = х(х - 1)(х + 2) 2 и неравенство (*) может быть записано в виде
х(х –1)(х + 2)2 > 0.
Решение.
Слайд 10
Рассмотрим функцию у= х(х-1)(х+2)2
Область определения функции D(у) =(-∞;
Найдем нули функции. х(х-1)(х+2)2 =0
Х=-2 Х=0 Х=1
4.Определим знак на каждом промежутке.
у>0, при х∈(-∞; -2) ∪ (-2; 0) ∪ (1; ∞).
Ответ: х∈(-∞; -2) ∪ (-2; 0) ∪ (1; ∞).
Слайд 13
Решение: Прибавляя к обеим частям неравенства 1, получим неравенство
х2(х2 – х – 2) < 0.
-1 0 2 х
Множество решений последнего неравенства находится методом интервалов: х∈( -1;0)∪(0;2).
Ответ: х∈(-1;0)∪(0;2).
Слайд 15Пример: Решить неравенство
⏐х2 - 2⏐ + х < 0.
Слайд 16Предположим, что х2–2≥0,
тогда неравенство принимает вид х2+х–2
2) Предположим, что х2–2<0, тогда согласно определению абсолютной величины имеем ⏐х2-2⏐=2–х2, и неравенство приобретает вид 2–х2+х<0.
Пересечение множества решений этого неравенства и неравенства
х2–2<0 дает второе множество решений исходного неравенства:
х∈(- √2; -1).
Объединяя найденные множества решений, окончательно получаем х∈(-2; -1).
Ответ: х∈(-2; -1).
Слайд 19Неравенства с параметрами.
Пример: Для всех значений а решить неравенство aх>1/x.
Решение: Запишем
тогда исходное неравенство равносильно двум системам неравенств:
ax2 – 1 > 0, ax2 – 1 < 0,
x > 0; x < 0.
Рассмотрим первую систему. Первое неравенство запишем в виде: ax2>1.
При а>0 оно равносильно неравенству х2>1/a, множество решений которого х<-1/√a и x>1/√a . В этом случае решение первой системы: х∈(1/√a;∞). При а≤0 левая часть неравенства ах2–1>0 отрицательна при любом х и неравенство решений не имеет, а следовательно, не имеет решений и вся система неравенств.
Рассмотрим вторую систему. При а > 0 решениями неравенства ах2 – 1<0 будут значения х∈(-1/√a; 1/√a), а решениями системы ⎯ значения х∈(-1/√a;0). При a≤0 левая часть неравенства
ах2–1<0 отрицательна при любых значениях х, т.е. это неравенство выполняется при всех х∈R и, следовательно, решениями системы будут значения х∈(-∞; 0).
Слайд 20Приведем графическую иллюстрацию решения этого примера.
а ≤ 0
Ответ: Если
Слайд 22Графическое решение неравенств.
Пример. Решить графически систему неравенств
x2+у2–4>0,
x>0.
Решение. Решение первого неравенства системы есть координаты точек плоскости, которые лежат вне окружности х2+у2=4; решение второго неравенства есть координаты точек верхней полуплоскости; решение третьего неравенства есть координаты точек правой полуплоскости.
Решением системы являются координаты точек, которые лежат в заштрихованной области.